Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Linearity in MDOF Models
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're discussing the limitations of linear MDOF models. Let's start with the assumption of linearity. Can anyone tell me what it means for a model to be linear?
It means that the model assumes a direct relationship between inputs and outputs, like if you double the force, you double the response, right?
Exactly! This assumption works well for small loads, but what happens when the load becomes severe?
The model might not accurately represent how the materials behave because they could start to yield or deform in ways that are not linear.
That's correct! When we experience severe ground motions, materials can behave in an unpredictable manner, leading to the need for nonlinear models.
So if we rely only on linear models, we might underestimate the risks during an earthquake?
Absolutely! In fact, this can result in structures failing when they're needed the most.
Material and Geometric Nonlinearities
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, let's explore material and geometric non-linearities. Who can explain what that involves?
I think it involves changes in the material properties, like going from elastic to plastic behavior when the structure is overloaded.
Exactly! And geometric nonlinearity refers to when the geometry of the structure changes due to deformation, which can affect its response. Why is this important in real-world scenarios?
Because if we ignore these changes, we might miscalculate how a structure will perform in a real earthquake.
Right! This is one of the reasons linear models can be inadequate for seismic analysis.
Non-Classical Damping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s talk about damping. What do we mean by classical damping?
Classical damping assumes that the force acting on a structure is proportional to its velocity, right?
That’s correct! But not all structures follow this assumption. Can anyone give an example of when damping might be non-classical?
Like in structures with complex connections or damping systems, where the behavior changes with response or time?
Exactly! Non-classical damping affects how a structure dissipates energy during movements, making it vital to account for in analysis.
Soil-Structure Interaction
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, let’s discuss soil-structure interaction. Why do we need to consider this when analyzing structures with MDOF models?
Because the soil can change the way a structure moves and reacts to forces, especially during an earthquake!
Yes! If we neglect soil-structure interaction, we might create models that do not reflect real behavior during seismic events.
So, engineers need to factor in the variability of soil conditions in their design?
Exactly! Understanding these interactions helps in creating safer, more reliable structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the primary limitations of linear MDOF models in structural analysis. Key issues include the assumption of linear behavior, the neglect of material and geometric non-linearities, and the lack of accurate representation of damping and soil-structure interactions. These limitations necessitate the use of more advanced analysis techniques like nonlinear time history or pushover analysis in performance-based design.
Detailed
Limitations of Linear MDOF Models
Linear Multi-Degree-of-Freedom (MDOF) models, while useful in many contexts for understanding structural dynamics, possess significant limitations when employed in seismic analysis and design.
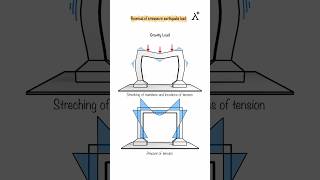
- Assumption of Linearity: Linear models assume a stable, proportional relationship between stress and strain which breaks down under severe ground motion. As ground motion intensity increases, materials may behave non-linearly, requiring more sophisticated models.
- Neglect of Material and Geometric Nonlinearities: Real structures often undergo changes that can affect their response, such as plastic deformation, buckling, and other nonlinear effects that are not captured in a linear analysis.
- Non-Classical Damping: Many structures do not exhibit the classical damping assumptions that linear MDOF models rely on. In reality, damping can be non-classical, meaning it varies based on structural response and loading conditions.
- Soil-Structure Interaction: Linear MDOF models typically do not adequately consider interactions with the surrounding soil, which can significantly influence the dynamic behavior of structures during earthquakes.
As a result, for performance-based design in earthquake engineering, it's crucial to invoke nonlinear analysis methods such as nonlinear time history analysis or pushover analysis to accurately capture the actual performance of structures under extreme conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Assumption of Linearity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Assumes linearity, which is not valid for severe ground motions.
Detailed Explanation
Linear MDOF models operate under the assumption that the structure's response to forces is proportional to the applied forces. However, during severe ground motions, such as earthquakes, this assumption fails. The material may yield or behave non-linearly, which means that the actual response may be significantly different from the predictions made by linear models.
Examples & Analogies
Imagine bending a rubber band — if you stretch it gently, it returns to its original shape (linear behavior). But if you stretch it too far, it may not return to its original shape and might even break (non-linear behavior). This illustrates how real materials can behave differently under extreme conditions than what simple models predict.
Neglecting Material and Geometric Nonlinearities
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Ignores material and geometric nonlinearities.
Detailed Explanation
Linear MDOF models also fail to account for material and geometric nonlinearities, which are critical in real-world applications. Material nonlinearity refers to how materials can change their properties under stress, while geometric nonlinearity refers to changes in the structure's shape or configuration when subjected to loads. These factors can significantly affect a structure's performance, especially during extreme events like earthquakes.
Examples & Analogies
Think about a paper airplane. When you first throw it gently, it flies according to predictable paths. However, if you throw it hard, the wings might bend or twist due to stress, changing how it flies. This reflects how real structures change behavior under heavier loads, something linear models do not capture.
Complex Damping Features
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Real structures have non-classical damping and interaction with soil, not captured in basic MDOF models.
Detailed Explanation
Linear MDOF models often assume a simple form of damping (classical damping), which may not reflect the complex interactions in real-world scenarios. Real structures can exhibit non-classical damping behavior where damping varies with frequency or is influenced by soil-structure interactions. This complexity is crucial for accurately predicting how a structure will respond to dynamic loads.
Examples & Analogies
Consider riding in a car on a bumpy road. The car's suspension (damping) adjusts differently depending on the bumps (soil interactions). In a poorly modeled system, these variations could lead to an inaccurate understanding of how comfortable the ride will be. Similarly, failing to account for these complexities can lead to unsafe building designs that perform poorly under load.
Need for Advanced Analysis Techniques
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Requires nonlinear time history analysis or pushover analysis for performance-based design.
Detailed Explanation
Because linear MDOF models are limited, engineers often need to use more sophisticated methods like nonlinear time history analysis or pushover analysis. These techniques allow for a more comprehensive understanding of structural behavior under dynamic loading, especially in the context of performance-based design, where meeting specific resilience criteria is crucial.
Examples & Analogies
Think of baking a cake; if you only follow a basic recipe (linear model), you might end up with a flat cake (inaccurate results). To get the desired flavor and texture (real structural response), you might need to adjust the baking time and temperature based on how the ingredients react when mixed (nonlinear analysis). This ensures the final product meets expectations in real situations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linearity in MDOF models: Assumes proportional response to loading, which is not valid for extreme loads.
-
Material and Geometric Nonlinearities: Real structures can undergo changes in behavior not captured by linear models.
-
Non-Classical Damping: Damping behavior may vary under different loading conditions and cannot always be modeled using classical damping.
-
Soil-Structure Interaction: The influence of the soil on structural behavior is crucial during seismic events and often disregarded in basic linear models.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of a linear model failing during an earthquake is the collapse of buildings that do not account for nonlinear behavior, leading to catastrophic damage.
-
Another example can be seen in high-rise buildings built on variable soil types; failing to consider soil interaction can lead to unexpected oscillations or structural failure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Models that are linear, don’t capture the strain, / In quakes they may falter, causing much pain.
📖 Fascinating Stories
-
Imagine a tall building swaying in a storm; it represents linear behavior, but when the winds are high, it bends in ways that were never foreseen. Only a nonlinear model can tell that tale.
🧠 Other Memory Gems
-
LMD (Linear MDOF Limitations): L for Linearity, M for Material Nonlinearity, D for Damping differences.
🎯 Super Acronyms
SISO (Soil Interaction for Structural Output) - highlighting the importance of soil-structure dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Model
Definition:
A model that assumes a constant proportional relationship between input and output, which applies only to small deformations.
-
Term: Material Nonlinearity
Definition:
The behavior of materials that change from elastic to plastic deformation under high stress.
-
Term: Geometric Nonlinearity
Definition:
The change in the structural geometry due to large deformations that affect its response.
-
Term: Damping
Definition:
The effect that reduces oscillations in a structure, often modeled as proportional to velocity in classical damping assumptions.
-
Term: SoilStructure Interaction
Definition:
The effects of soil conditions on the behavior of a structure, especially during external dynamic loading such as earthquakes.