Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will explore Multi-Degree-of-Freedom systems, or MDOF systems. Can anyone tell me how these differ from Single-Degree-of-Freedom models?
MDOF systems allow for multiple points of independent movement, right?
Exactly! MDOF models are crucial for structures like buildings and bridges that can experience dynamic loads at multiple locations. Can anyone think of a scenario where SDOF would fail?
Maybe during an earthquake, where different parts of a structure move differently?
Great point! Earthquake forces can induce various responses throughout a structure. This is where MDOF systems shine. Remember, MDOF accounts for the interconnected nature of structural components.
How do we actually calculate the responses for MDOF systems?
Good question! We'll learn about mathematical modeling—specifically, the mass, stiffness, and damping matrices—let's keep that in mind.
Can you summarize what we learned today?
Sure! We established the foundation for understanding MDOF systems, their importance in capturing the dynamics of complex structures, and we'll explore how to model their behavior mathematically next.
Degrees of Freedom
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s dive deeper into degrees of freedom in MDOF systems. Who can explain what a degree of freedom means in this context?
It’s the number of independent movements a structure can make?
Correct! Each movement is a degree of freedom. For instance, in a multi-storey building, each floor typically represents one translational DOF. How many DOFs would a five-story building have?
Five, for each floor?
Exactly! And we can also consider rotational degrees of freedom in frame structures. This is crucial for understanding how different elements interact during dynamic loading.
So, if every floor is a DOF, what happens in an earthquake?
Excellent thought! In an earthquake, different floors can sway independently of one another, leading to a complex dynamic response.
Can you recap the key points of DOF?
Certainly! A degree of freedom indicates independent movements in structures. MDOF systems adequately account for these movements, especially in complex loads like earthquakes. Next, we will discuss how these are mathematically modeled!
Mathematical Modeling of MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s explore how we mathematically model MDOF systems. Can anyone describe the role of mass, stiffness, and damping matrices?
Are they used to represent the structure’s response to forces?
Precisely! The mass matrix contains the masses at each DOF, the stiffness matrix represents the structural stiffness, and the damping is vital for energy dissipation. Let’s look at the equations of motion for a damped system.
I remember it as [M]{ü(t)}+[C]{u˙(t)}+[K]{u(t)}={f(t)}. What do all those symbols mean?
Great recall! Here, {u(t)} is displacement, {u˙(t)} is velocity, {ü(t)} is acceleration, and {f(t)} denotes external forces acting on the system. Why do you think we represent these terms as vectors?
Because multiple degrees of freedom can occur simultaneously?
Exactly! Each vector encapsulates the behavior of the entire system with n DOFs. As we continue, you’ll see how this leads us to solutions in free vibration analysis.
Can we summarize the mathematical models discussed?
Sure! MDOF systems use mass, stiffness, and damping matrices for dynamic response modeling. Understanding these components is key to analyzing structures under various loads.
Modal Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let’s delve into modal analysis. Who understands its role in MDOF systems?
Isn’t it a way to simplify the analysis by breaking it down into modes?
Exactly! Modal analysis helps us treat each mode as a separate SDOF system, which makes calculations manageable. Can anyone describe why this is particularly useful?
It allows us to analyze complex vibrations more simply, right?
Spot on! The total response can be obtained using modal superposition, which combines the effects of each mode. How about the eigenvalue problem? What does it help us find?
It helps find natural frequencies and mode shapes, defining how the structure will behave.
Correct! The eigenvalues represent squared natural frequencies, and the eigenvectors represent the mode shapes. These are crucial during design and analysis phases.
Can you summarize the main points of modal analysis?
Certainly! Modal analysis simplifies MDOF systems into SDOF analysis by using natural frequencies and mode shapes, making it invaluable in vibration analysis.
Applications and Practical Aspects
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, let’s discuss some applications of MDOF systems. Who can name one major reliance of these models?
Seismic design and analysis of buildings!
Right! They are also used in assessing the impact of dynamic forces in bridges. However, what are some limitations we need to be aware of?
They assume linear behavior, which may not apply to extreme conditions.
Exactly! Nonlinearities in real-world systems often require more sophisticated modeling techniques. Why is understanding this crucial for engineers?
So we can create safer structural designs that consider real-life conditions.
Well said! Remember, while MDOF systems are powerful tools in structural engineering, it’s essential to use them with an understanding of their scope and limitations.
Can you summarize what we discussed in this session?
Certainly! MDOF systems have broad applications in seismic analysis and design, but they also have limitations related to linear assumptions. Keeping these in mind allows us to improve our designs effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the significance of MDOF systems in accurately modeling the dynamic responses of real-world structures, discussing degrees of freedom, mathematical modeling, modal analysis, and damping considerations in the context of seismic loading.
Detailed
Detailed Summary
In real-world engineering applications, such as buildings and bridges, structures often cannot be effectively modeled using single-degree-of-freedom (SDOF) systems due to their complex interdependencies. Instead, Multi-Degree-of-Freedom (MDOF) systems allow for a more accurate representation of a structure's behavior under dynamic loads, particularly in earthquake engineering.
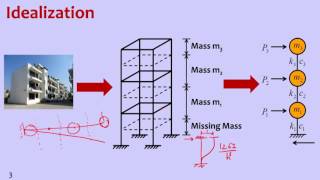
Degrees of Freedom (DOF): Each floor of a building typically contributes a degree of freedom in a lumped mass model, reflecting the independent motion of the structure. For instance, a multi-storey building modeled for planar analysis will have a translational DOF for each floor (n floors = n DOFs).
Mathematical Modeling: The MDOF systems are mathematically represented through assembled mass, stiffness, and damping matrices, capturing the structure's response to external forces. The equations of motion detail both undamped and damped systems, leading to the eigenvalue problem that facilitates modal analysis.
Modal Analysis: This key technique enables engineers to treat each mode of the system as an independent SDOF system. The total response of the structure is computed via modal superposition, which combines the effect of each mode while addressing seismic excitations.
Damping Factors: The section delves into classical and non-classical damping considerations, emphasizing the analytical limitations of the MDOF model assumptions. It also covers numerical solution strategies for complex structures, base isolation techniques for earthquake resilience, and the impact of torsional effects in irregular buildings.
In summary, understanding MDOF systems is crucial for civil engineers to model effectively, analyze, and design safe structures capable of resisting seismic forces.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Multi-Degree-of-Freedom (MDOF) Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In real-world structures such as buildings, bridges, and towers, the dynamic response to ground motion or external forces cannot be accurately captured using single-degree-of-freedom (SDOF) models alone. These structures have multiple interconnected components (floors, frames, columns, etc.), each of which can move independently in response to dynamic loading.
Detailed Explanation
MDOF systems are essential for analyzing structures that have complex interactions due to multiple components. Unlike SDOF models that assume the entire structure moves as one unit, MDOF models consider each part's ability to move independently. For instance, in a tall building during an earthquake, different floors may experience different amounts of shaking, requiring a model that can capture these variations.
Examples & Analogies
Think of MDOF systems like a team of dancers performing on stage. While one dancer (SDOF) represents one movement, the entire team (MDOF) showcases a variety of movements and interactions, reflecting how the dancers respond to music and one another.
The Importance of MDOF Models in Earthquake Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Hence, Multi-Degree-of-Freedom (MDOF) models are essential for realistic dynamic analysis, especially in Earthquake Engineering, where lateral loads and seismic excitations act simultaneously on different points of a structure.
Detailed Explanation
MDOF models provide a more accurate representation of how buildings respond to earth tremors. They allow engineers to predict how different parts of a structure will move during an earthquake, leading to better safety designs. This is particularly important because different floors or elements of a building might react differently to seismic forces, and a one-size-fits-all (SDOF) approach would overlook these critical nuances.
Examples & Analogies
Imagine an orchestra, where each instrument contributes differently to the overall sound. If you only focus on a single instrument (SDOF), you miss the richness of the entire orchestra (MDOF). In an earthquake, just like an orchestra, different parts of a building contribute uniquely to its safety and stability.
Key Attributes of MDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
MDOF systems represent structures with more than one coordinate (degree of freedom) required to define their motion. This chapter introduces the formulation, characteristics, and behavior of MDOF systems, particularly in the context of linear elastic analysis under dynamic loading.
Detailed Explanation
Each degree of freedom in an MDOF system corresponds to a specific way a structure can move or deform. For example, in a multi-story building, each floor can be treated as having its own degree of freedom in horizontal motion. Understanding these coordinates is crucial for analyzing the structural behavior under loads, especially during dynamic conditions like earthquakes.
Examples & Analogies
Consider a trampoline. As multiple people jump on it, each individual's jump (degree of freedom) affects how the entire trampoline responds. Similarly, in MDOF systems, understanding each component's individual motion helps in predicting overall behavior under stress.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
MDOF Systems: Necessary for modeling multi-component structures under dynamic loads.
-
Degrees of Freedom: Independent displacements or rotations in a structure.
-
Mathematical Modeling: Utilizes mass, stiffness, and damping matrices.
-
Modal Analysis: Simplifies the dynamic response by analyzing modes.
-
Base Isolation: A technique to protect structures from seismic forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A five-story building has five translational degrees of freedom, each representing the independent motion of that floor under dynamic loads.
-
The use of modal analysis reduces a complex MDOF problem into simpler SDOF models for each mode during seismic analysis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If you see a building sway, remember MDOF is here to stay.
📖 Fascinating Stories
-
Imagine a bridge where each part sways like dancers; each dancer listens to the music of the ground, moving together yet independently.
🧠 Other Memory Gems
-
MATH: M = Mass matrix, A = Analysis, T = Torsional effects, H = Harmonic responses.
🎯 Super Acronyms
FIND
- F: = Freedom (Degrees)
- I: = Interconnected (Components)
- N: = Natural frequencies
- D: = Damping (Effect).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: MultiDegreeofFreedom (MDOF) Systems
Definition:
Structural systems with multiple independent coordinates to define motion; crucial for analyzing complex behaviors under dynamic loads.
-
Term: Degree of Freedom (DOF)
Definition:
The number of independent displacements or rotations required to describe the state of a system.
-
Term: Mass Matrix
Definition:
A diagonal matrix that contains the mass values at each degree of freedom in a dynamic system.
-
Term: Stiffness Matrix
Definition:
A matrix that represents the stiffness characteristics of a system, crucial for dynamic analysis.
-
Term: Damping Matrix
Definition:
A matrix used to account for the energy dissipation in a system during dynamic loading.
-
Term: Eigenvalue Problem
Definition:
A mathematical formulation that arises when solving for natural frequencies and mode shapes of dynamic systems.
-
Term: Modal Analysis
Definition:
A technique used to analyze the dynamic characteristics of a system by decomposing it into simpler modes.
-
Term: Modal Superposition
Definition:
A method of combining modal responses of a structure to determine the total response under dynamic loading.
-
Term: Base Isolation
Definition:
A seismic protection strategy that decouples a structure from ground motion through isolators.
-
Term: Torsional Effects
Definition:
The responses that arise in structures due to asymmetrical loading, leading to twisting and increased stresses.