Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Pressure in Fluids
Unlock Audio Lesson
Today, we're going to dive into how pressure behaves in stationary fluids. Who can tell me what happens to shear stress when a fluid is at rest?
The shear stress becomes zero.
Exactly! So, what does that imply about the forces acting on our control volume?
Only normal stress, which is equal to pressure, is acting on the surface.
Great! Let's remember that with the acronym 'PANS' - Pressure Acts Normal to Surfaces. Now, can anyone tell me the significance of the body force from gravity?
It contributes to how pressure increases with depth.
Absolutely! Pressure increases as we go deeper into the fluid due to the weight of the fluid above. Let's move on to how we express pressure mathematically.
Hydrostatic Pressure Distribution
Unlock Audio Lesson
We can express pressure as a function of coordinates, \( P(x, y, z) \). Who can tell me how we approximate pressure at different points in a fluid?
Using Taylor series?
Exactly! The Taylor series allows us to express the pressure at nearby points and helps us derive the hydrostatic equation. Remember this with 'TAYLOR' - To Approximate Yielding Linear Observations of Ratios. Now, what do we know about pressure variation in horizontal versus vertical directions?
Pressure is constant in horizontal directions and varies in the vertical direction.
Good! This gives rise to the hydrostatic equations, where pressure change is primarily a function of the vertical axis because of gravity.
Applications and Practical Insights
Unlock Audio Lesson
We've covered a lot about hydrostatic equations. How about discussing where these concepts apply in real life?
They're used in engineering for designing dams and understanding fluid pressures.
Absolutely! And how do we observe pressure changes in the atmosphere using barometers?
By measuring how high mercury rises in a tube.
Great! This is a classic example of applying hydrostatics to measure atmospheric pressure. Let's wrap up what we've learned today.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on how to determine the pressure field in a stationary fluid, focusing on pressure as a function of spatial coordinates and the forces acting on a control volume. Key concepts include body forces, surface forces, and different types of pressure measurements.
Detailed
Hydrostatic Equations
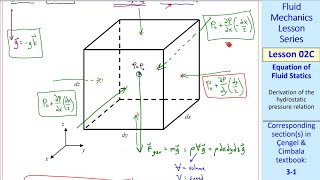
In this section, we explore the crucial topic of hydrostatic equations, which govern the behavior of fluids at rest. The pressure field in a fluid can be described as a function of spatial coordinates: \( P = P(x, y, z) \). When examining a control volume (often imagined as a parallelepiped), we note that shear stresses are absent since the fluid is static. This leads to pressure being the primary force acting normal to the surfaces of the control volume.
Two forces must be considered: surface forces (arising from pressure) and body forces (like gravity). The volume of the control volume multiplied by the unit weight of the fluid gives the body force component. Using Pascal's law, pressure acts perpendicularly to each surface of the control volume.
The pressure can be approximated spatially using Taylor series, allowing us to express pressure variation at different points in space. This leads us to the fundamental hydrostatic equations, which can be simplified to showcase that pressure primarily varies along the vertical axis (z-direction) due to gravitational forces, while remaining constant horizontally (x and y directions).
The section concludes by discussing gauge pressure versus vacuum pressure, emphasizing the reference point for pressure measurements, which can either be atmospheric pressure or absolute vacuum. Understanding these concepts aids in pressure distribution calculations, essential for applications like barometers and capillary action.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Pressure Field in a Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
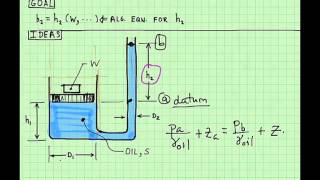
Now if I go for the next ones that how to get the pressure field when fluid is at the rest. That means I am just looking the what could be the functions of the P, P = P (x, y, z).
Detailed Explanation
This chunk introduces the concept of pressure in a fluid that is at rest, indicating that pressure can be defined as a function of its spatial coordinates (x, y, z). Essentially, it sets the foundation for understanding how pressure behaves in a static fluid scenario, where no motion is occurring, and hence shear stress is non-existent.
Examples & Analogies
Imagine a still pond. The pressure at any point below the surface can be thought of as depending on the distance from the surface. It varies with depth, but at any given depth, it's consistent across the pond, just like the pressure at point P is consistent in the fluid's control volume.
Control Volume and Shear Stress
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If it that it is now again I am considering a very simple case, let us consider a control volume like this okay. This is what my control volume. As I said it when the fluid is at rest the shear stress become zero. So there is no shear stress component on this fluid plane. Only this normal stress which is as equivalent to the pressure will act over this control surface.
Detailed Explanation
This section explains that when dealing with a fluid at rest, one can assume a control volume for analysis. Within this control volume, shear stress is absent, meaning that the forces acting on it are purely normal forces (due to pressure). This is crucial because it simplifies the analysis of fluid behavior.
Examples & Analogies
Think of a glass of water sitting on a table. The water is calm; there are no waves or currents. The only forces acting on the bottom of the glass are the weight of the water above and the atmospheric pressure acting on the surface. This is similar to how pressure acts in the control volume.
Gravity's Influence on Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The pressure at the centre of the fluid control volume is assumed to be P (x, y, z). At that point, the gravity force is acting it which is the body force component.
Detailed Explanation
In a fluid at rest, gravity exerts a force on the fluid. This force is responsible for the pressure gradients observed within the fluid. The pressure at a certain point in the fluid (P(x, y, z)) reflects the influence of this gravitational force acting over the fluid's volume. The body force is often expressed as the product of fluid density and gravitational acceleration, indicating how pressure increases with depth due to the weight of the fluid above.
Examples & Analogies
Consider diving into a swimming pool. The deeper you go, the more pressure you feel. This increased pressure is due to the weight of the water above you—the force of gravity acting through the water’s mass.
Pressure Acting on Control Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
pressure acts normal to the surface. So that what we can consider pressures act there normal to the surface. Then we need to define now as a pressure as a x, y, z is a pressure field what we are looking it which is a function of x, y, z.
Detailed Explanation
This part discusses how pressure acts specifically on the control surfaces of the fluid. The use of normal force implies that pressure exerts a force perpendicular to any surface in contact with the fluid. As we continue, we focus on how pressure can be assessed as a function of spatial coordinates, allowing us to model how pressure distributes across different points within the fluid system.
Examples & Analogies
Think about holding a beach ball underwater; the water presses in from all sides. The pressure you're resisting from the water is acting perpendicular to your hand, demonstrating how pressure acts normally to surfaces.
Functional Relationships and Taylor Series Approximation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
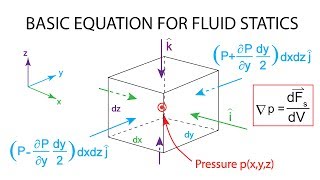
I can use Taylor series to approximate distance of this surface which is a far away from. The pressure at point on the surface can be expressed as...
Detailed Explanation
Here, the discussion shifts to using mathematical tools, such as Taylor series, to model how pressure changes concerning distance from a specific point (like the center of the control volume). This approximation helps us understand pressure variations across a surface in a more manageable form, which can be particularly useful for applications in engineering and physics.
Examples & Analogies
Imagine trying to estimate the height of a tree from a distance. By knowing the height at a nearby point and using simple geometry (like a triangle), you can predict the height further away. Similarly, Taylor series helps estimate how pressure behaves at different points based on known values.
Pressure Gradient and Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If this is the pressure is acting on the surface, similar way I can get it what will be pressure is acting. I know this pressure multiply the area over these simplified control volumes, I will get the force component. That what is acting along the y directions.
Detailed Explanation
This section explains how to calculate the force exerted by pressure acting on a surface area. By multiplying the pressure by the area of the control surface, one can derive the resultant force component. This principle is essential in hydrostatics and aids in understanding how forces interact within a fluid at rest.
Examples & Analogies
If you've ever pressed down on the bottom of a children’s swimming pool with your hand, you've felt the force of the water pressing back against your palm. The pressure of the water multiplied by the area of your hand gives you the total force you're resisting.
Total Force Balance and Hydrostatic Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As the fluid is rest, the sum of the force should be equal to zero. That the vector is equal to zero and that field what we will get it this part and is finally the ∇...
Detailed Explanation
In this part, it is emphasized that in a static fluid, the sum of all forces acting on a control volume must equal zero to maintain equilibrium. This leads to the derivation of hydrostatic equations, which describe how pressure varies with depth in a fluid. These equations simplify the analysis of forces in a hydrostatic environment and are foundational for fluid mechanics.
Examples & Analogies
Think of a balloon filled with water. If it’s not moving, the forces (the water pressing against the inside of the balloon and the balloon’s elasticity pushing back) balance out perfectly. If they did not, you'd see changes—equal forces result in stability.
Gauge Pressure and Vacuum Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now the point is what we are going to discuss is that gauge pressure and vacuum pressure. Components now is coming it what is your datum to measure the pressure.
Detailed Explanation
This section introduces gauge pressure and vacuum pressure concepts. Gauge pressure is the pressure reading that is above atmospheric pressure, while vacuum pressure is below atmospheric pressure. It discusses the importance of establishing a reference point (datum) for pressure measurements, which can significantly influence interpretations of pressure in various scenarios.
Examples & Analogies
When you inflate a tire, the gauge pressure tells you how much air is in the tire above the surrounding atmosphere. If you measure vacuum pressure in a sealed container, you're determining how much lower the pressure is than the atmospheric pressure outside.
Measuring Absolute Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you need to compute it what will be the absolute pressure, then it is a very easy. You just use whether the gauge pressure or this the vacuum pressure that difference what we can get it that what you just add with atmospheric pressure to get the absolute pressure.
Detailed Explanation
Here, the process for calculating absolute pressure is clearly laid out. To find absolute pressure, you can either add gauge pressure to atmospheric pressure when the gauge pressure is above atmospheric levels, or subtract the vacuum pressure from atmospheric pressure when it is below. This combination helps in understanding the total stress exerted on an object by the fluid.
Examples & Analogies
Consider a soda can. When you open it, the pressure inside (initially higher than atmospheric because of carbonation) is what you feel when the gas rushes out. The absolute pressure would be the combination of how much that pressure exceeds the atmospheric pressure.
Pressure Distribution in a Fluid
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now as we derive pressure distribution equations which in vector forms and let we simplify that equations...
Detailed Explanation
This part concerns the process of deriving pressure distribution equations, which can be expressed in vector forms. When gravity is aligned with a certain coordinate system, it leads to the conclusion that pressure only varies along that particular axis (commonly the z-axis), reinforcing the idea that pressure remains constant across horizontal planes in a static fluid.
Examples & Analogies
Think of a column of water. If you go from the top down, the pressure increases due to the weight of the water above. However, if you look at any horizontal layer of that water, the pressure remains the same regardless of where you take that measurement—much like a level surface of a bathtub full of water.