Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Pressure Forces
Unlock Audio Lesson
Today, we'll discuss how pressure works when fluids are at rest. Can anyone tell me what pressure is?
Isn't pressure the force applied perpendicular to a surface?
Exactly! Pressure is indeed a normal force acting on a surface. Now, when fluid is at rest, there's no shear stress, only normal stress. This leads us to Pascal's law. Can someone explain what Pascal's law states?
Pascal's law says that pressure applied to an enclosed fluid is transmitted undiminished.
Very well! Remember, the pressure in a fluid acts equally in all directions in a confined space, allowing us to measure it effectively using various devices.
What about body forces like gravity?
Great question! Body forces, such as gravity, affect pressure as well. If we consider a control volume, gravity acts downwards, contributing to the pressure gradient. Remember, we're summarizing forces acting on a fluid, which includes both pressure and body forces.
So the overall pressure in a fluid is a combination of these forces?
Exactly! That's crucial for understanding fluid mechanics. Let’s summarize: Pressure is a normal force, and Pascal's law indicates it transmits uniformly. Body forces like gravity add complexity to our pressure analysis.
Differentiating Gauge Pressure and Vacuum Pressure
Unlock Audio Lesson
Now let's talk about how we measure pressure effectively. Can anyone tell me what gauge pressure is?
I think gauge pressure is the pressure above atmospheric pressure.
Exactly! Gauge pressure is measured relative to atmospheric pressure, which we consider as a reference point. What about vacuum pressure?
Vacuum pressure is below atmospheric pressure, right?
Correct! So when you measure pressure, you can either reference the vacuum level, which is theoretically zero pressure, or the local atmospheric pressure. Could you explain how we usually measure atmospheric pressure?
Using a mercury barometer, right?
Yes! The mercury barometer measures atmospheric pressure by balancing the height of mercury against atmospheric force. What do we know about its use at higher altitudes?
The atmospheric pressure decreases, affecting measurements.
Absolutely correct! As altitude increases, atmospheric pressure decreases, which is why we feel different at high elevations. Keep this summary in mind: Gauge pressure is relative to local atmosphere, while vacuum pressure is below atmospheric.
Pressure Distribution and Hydrostatic Equations
Unlock Audio Lesson
Let's now analyze how pressure varies with depth. What insights do we have about pressure change in a static fluid?
Pressure increases with depth due to the weight of the fluid above.
Correct! As we delve deeper into a fluid, the weight of the fluid above exerts more pressure. What does our hydrostatic equation suggest?
It indicates the pressure gradient in vertical direction.
Exactly! The pressure gradient is influenced by the density of the fluid and the acceleration due to gravity. Can someone summarize what we derived?
Pressure increases linearly with depth due to hydrostatic pressure.
Perfect! Remember, at any horizontal plane in a stationary fluid, pressure remains constant—a crucial concept for fluid mechanics.
The Role of Capillary Action
Unlock Audio Lesson
To finish up, let's touch on the capillary effect. Who can explain what happens when a thin tube is placed in a liquid?
The liquid rises in the tube due to surface tension?
Exactly! The competition between gravity and surface tension causes this phenomenon. Can someone explain how we derive the height of liquid in the tube?
By balancing the weight of the liquid against the surface tension?
You got it! This relationship can be quantified, and it is crucial in fields like biology and chemistry. Remember, capillarity occurs more significantly in narrow tubes. Who remembers why?
Because the smaller the diameter, the higher the rise?
Exactly right! So to conclude this session, capillary action combines gravity and surface tension, affecting fluid behavior in small spaces.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on how atmospheric pressure is measured, differentiating between gauge and absolute pressure. It touches upon fundamental principles such as Pascal's law, concepts of hydrostatic pressure, and the significance of control volumes in analyzing pressure distributions in static fluids.
Detailed
Measurement of Atmospheric Pressure
In this section, we delve into the fundamentals of measuring atmospheric pressure. We start from a simple control volume where fluid is at rest, emphasizing that under static conditions, shear stress is zero, leaving only normal stress equivalent to pressure acting on surfaces.
Key Concepts:
- Pressure Field Representation: The pressure, represented as P(x, y, z), is a function of three Cartesian coordinates at a centroid within the fluid.
- Control Volume Analysis: By applying a Taylor series approximation, we analyze how pressure varies at different distances from a reference point.
- Body Forces and Surface Forces: The two essential forces in a fluid at rest include surface forces due to pressure gradients and body forces influenced by gravity.
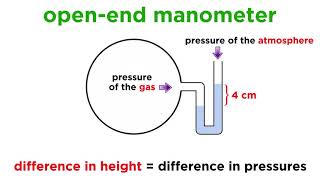
- Pressure Measurement Techniques: The section distinguishes between gauge pressure (above atmosphere) and vacuum pressure (below atmosphere), explaining the use of mercury barometers for measuring atmospheric pressure.
- Hydrostatic Equations and Gravity Effects: It introduces hydrostatic equations in vector form and simplifies them to understand variations along the vertical axis under the influence of gravity.
The section concludes by exploring practical applications, such as the effects of adjacent fluid reservoirs and capillary action, reinforcing the foundational concepts of fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Pressure at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if I go for the next ones that how to get the pressure field when fluid is at the rest. That means I am just looking the what could be the functions of the P, P = P (x, y, z). If it that it is now again I am considering a very simple case, let us consider a control volume like this okay. This is what my control volume. As I said it when the fluid is at rest the shear stress become zero.
So there is no shear stress component on this fluid plane. Only this normal stress which is as equivalent to the pressure will act over this control surface.
Detailed Explanation
When fluid is at rest, it means there are no movements affecting its state. In this condition, the fluid does not experience shear stress – it only has normal stress, which is directly proportional to the pressure exerted on the fluid's surface. This leads us to consider how pressure varies in a control volume, described mathematically as P(x, y, z). Understanding this forms the basis for studying how pressure is distributed in different fluid contexts.
Examples & Analogies
Think of a swimming pool. When there are no waves, the water is still, and the only pressure acting on the bottom of the pool is due to the weight of the water above it. Just like the still water in the pool, in a fluid at rest, pressure is evenly distributed based on the depth.
Components of Force Acting on Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The pressure at the centre of the fluid control volume is assumed to be P (x, y, z). At that point, the gravity force is acting it which is the body force component. The gravity force what will be there? It will be unit weight multiply the volume of the control volume, which is very simple things.
Detailed Explanation
Within the control volume, we not only have pressure acting but also the force of gravity, which acts as a body force. This gravitational force can be calculated by multiplying the unit weight of the fluid by the volume of that control volume. This relationship between pressure, gravity, and volume is crucial for understanding how pressure varies with depth in fluids.
Examples & Analogies
Consider a soda can filled with liquid. The weight of the liquid inside exerts pressure downwards due to gravity. When you shake it, some liquid might spill, showing how the weight (gravity) of the liquid directly affects the pressure exerted at the base of the can.
Pascal's Law and Pressure Variation in Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
All these pressure is going to act it as the Pascal law says that pressure acts normal to the surface. So that what we can consider pressures act there normal to the surface. Then we need to define now as a pressure as a x, y, z is a pressure field what we are looking it which is a function of x, y, z.
Detailed Explanation
According to Pascal's Law, pressure exerted on a fluid is transmitted equally in all directions and acts perpendicular (normal) to the surface of the fluid. In practical terms, as we define pressure in a three-dimensional space (x, y, z), we can understand how pressures vary at different points based on their spatial coordinates. This forms the foundation for understanding more complex fluid behaviors.
Examples & Analogies
Imagine using a syringe. When you push down on the plunger, the pressure you apply is evenly spread out throughout the fluid inside. The fluid then pushes against any surface it comes into contact with, demonstrating how pressure acts normal to surfaces.
Understanding Gauge and Vacuum Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now the point is what we are going to discuss is that gauge pressure and vacuum pressure. Components now is coming it what is your datum to measure the pressure. Whether you have to make a absolute zero pressure, that means you have a vacuum. From there you are measuring the pressure, or you consider as local atmosphere, to measure the pressure.
Detailed Explanation
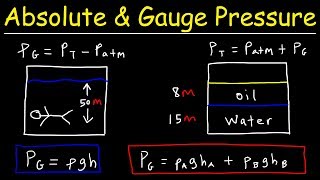
When discussing pressure measurement, we must determine our reference point or 'datum.' There are two primary forms of pressure measurement: gauge pressure, which refers to the pressure relative to local atmospheric pressure, and absolute pressure, which measures pressure relative to a perfect vacuum. This distinction is crucial for accurately understanding pressure in different contexts.
Examples & Analogies
Think of a car tire. The gauge pressure is what the tire pressure gauge reads compared to current atmospheric pressure; if it says 30 psi, it's 30 psi above the atmospheric pressure. Absolute pressure, on the other hand, would be 30 psi plus the weight of the atmosphere on top of it. This means the car tire may be under a much higher actual pressure than we feel.
Pressure Measurement with Barometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So when you measure the atmospheric pressure is a datum. There is a two conditions is comes it. One will be the pressure above the atmospheric pressure, another one will be the pressure below the atmospheric pressure.
Detailed Explanation
To measure atmospheric pressure, we use barometers, which can indicate the pressure above or below atmospheric levels. A common type is the mercury barometer, where the height of the mercury column can infer atmospheric pressure. Understanding these measures helps to predict weather changes and comprehend buoyancy and fluid dynamics better.
Examples & Analogies
Imagine an old-fashioned mercury barometer like the ones used many years ago. The glass tube filled with mercury would rise or fall based on the atmospheric pressure—much like how a tide rises and falls with the moon's gravitational pull. Just as you can predict high or low tides, atmospheric pressure can help forecast weather conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pressure Field Representation: The pressure, represented as P(x, y, z), is a function of three Cartesian coordinates at a centroid within the fluid.
-
Control Volume Analysis: By applying a Taylor series approximation, we analyze how pressure varies at different distances from a reference point.
-
Body Forces and Surface Forces: The two essential forces in a fluid at rest include surface forces due to pressure gradients and body forces influenced by gravity.
-
Pressure Measurement Techniques: The section distinguishes between gauge pressure (above atmosphere) and vacuum pressure (below atmosphere), explaining the use of mercury barometers for measuring atmospheric pressure.
-
Hydrostatic Equations and Gravity Effects: It introduces hydrostatic equations in vector form and simplifies them to understand variations along the vertical axis under the influence of gravity.
-
The section concludes by exploring practical applications, such as the effects of adjacent fluid reservoirs and capillary action, reinforcing the foundational concepts of fluid mechanics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of measuring gauge pressure using a tire pressure gauge, which reads pressure above atmospheric pressure.
-
Example of a mercury barometer demonstrating atmospheric pressure by balancing mercury against atmospheric force.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a tube, when you go deep, pressure rises, it's not cheap.
📖 Fascinating Stories
-
Imagine sailors using a barometer on a ship, watching mercury rise and fall with the changing weather, measuring the atmospheric pressure, keeping ships safe during storms.
🧠 Other Memory Gems
-
G.P. (Gauge Pressure) = A.P. (Atmospheric Pressure) + P (Pressure), remember 'GAP' whenever you think of gauge pressure!
🎯 Super Acronyms
PAST
- Pascal's law
- Atmospheric measurement
- Surface force
- Total pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Pressure
Definition:
Force per unit area exerted perpendicular to a surface.
-
Term: Gauge Pressure
Definition:
Pressure measured relative to atmospheric pressure.
-
Term: Vacuum Pressure
Definition:
Pressure below atmospheric pressure.
-
Term: Hydrostatic Pressure
Definition:
Pressure exerted by a fluid at equilibrium due to gravity.
-
Term: Pascal's Law
Definition:
A principle stating that a change in pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid.