Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatics
Unlock Audio Lesson
Today, we will discuss how pressure behaves in fluids at rest. Who can tell me what happens to shear stress in a stationary fluid?
Shear stress becomes zero, right?
Exactly! Without shear stress, only normal stress in the form of pressure acts on the fluid. Therefore, pressure is a function of the vertical position in the fluid.
Is pressure the same everywhere in a horizontal plane?
Good question! Yes, pressure remains constant across any horizontal surface under static conditions because it varies only with height.
Can you explain why it only varies vertically?
Certainly! It varies vertically due to gravitational effects acting on the weight of the fluid. The deeper you go, the greater the weight of the fluid above, resulting in increased pressure.
So we can use the equation P = ρgz to calculate pressure at a certain depth?
Exactly! And remembering that simplifies our calculations in fluid statics. Let's summarize: in a static fluid, shear stress is zero, pressure is constant in horizontal planes, and pressure increases with depth.
Pressure Measurements
Unlock Audio Lesson
Next, let's talk about how we measure pressure. Does anyone know the difference between gauge pressure and vacuum pressure?
Gauge pressure is the pressure above atmospheric pressure, right?
Correct! And vacuum pressure is measured below atmospheric pressure. It’s essential to know your reference point.
So if we measure pressure in a car tire, it's gauge pressure?
Yes, because it’s measured above atmospheric pressure. Now, can anyone give an example of how we might apply this in real life?
Using a barometer to measure atmospheric pressure?
Absolutely! The mercury barometer is a classic example for measuring atmospheric pressure with a vacuum at the top of the column.
Will the height of the mercury change with altitude?
Yes! Pressure decreases with altitude, leading to lower mercury heights in barometers at higher elevations. Let’s summarize: Gauge pressure is above atmospheric, and vacuum pressure is below. And remember: atmospheric pressure changes with altitude.
Applications and Equations
Unlock Audio Lesson
Now, let’s calculate pressure at different depths using the formula P = ρgz. Who can tell me what these variables represent?
ρ is the density of the fluid, g is gravity, and z is depth.
Exactly! Let’s say we have water with a density of 1000 kg/m³ and we want to calculate the pressure 10 m underwater. Can anyone calculate this?
P = 1000 kg/m³ * 9.81 m/s² * 10 m = 98100 Pa!
Spot on! That’s the pressure at that depth. Who can tell me how this relates to our previous discussion about static pressure in horizontal planes?
The pressure remains constant across any horizontal surface, no matter where you are at that depth.
Exactly right! Summarizing today, we’ve applied P = ρgz for practical calculations and discussed pressure distribution in horizontal planes.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on pressure fields in a fluid at rest, indicating that under hydrostatic conditions, pressure only varies vertically (z-direction) due to gravity, while it remains constant across horizontal planes. It also explores concepts like gauge pressure, vacuum pressure, and presents various equations illustrating these principles.
Detailed
Pressure Variation in a Horizontal Plane
This section explores the behavior of pressure in fluids at rest, specifically in a hydrostatic scenario. When a fluid is at rest, it experiences no shear stress, meaning that pressure is the only normal stress acting on control surfaces. The pressure is defined as a function of three coordinates, P(x, y, z), allowing for analysis in Cartesian coordinates.
Hydrostatic Pressure Distribution
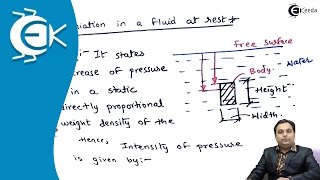
According to Pascal's principle, pressure within a static fluid acts equally in all directions, leading to pressure only varying with respect to the vertical height (z-coordinate). In a horizontal plane (x-y plane), the pressure remains constant across the surface. When deriving the pressure components, the weight of the fluid column above a point in the fluid body must be considered alongside surface forces. The relationship between pressure and height is linearly proportional, which can be understood through the following equation:
- Pressure at a distance z: P = ρgz
where ρ is the fluid density and g represents the acceleration due to gravity.
Gauge and Vacuum Pressure
The text also introduces the concepts of gauge pressure and vacuum pressure, explaining how these relate to atmospheric pressure measurements. Gauge pressure is the pressure above atmospheric pressure, while vacuum pressure refers to pressure below atmospheric conditions. This duality emphasizes the importance of establishing a datum when measuring pressure. The section concludes with examples and practical applications to reinforce these concepts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Pressure in a Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if I go for the next ones that how to get the pressure field when fluid is at the rest. That means I am just looking the what could be the functions of the P, P = P (x, y, z). If it that it is now again I am considering a very simple case, let us consider a control volume like this okay. This is what my control volume. As I said it when the fluid is at rest the shear stress become zero.
Detailed Explanation
When discussing pressure in a fluid at rest, we start by defining the control volume where we analyze the fluid's behavior. In a control volume, the pressure, denoted as P, can be expressed as a function of the coordinates x, y, and z. It is important to note that, in this state, the fluid has no shear stress acting on it, meaning the only forces we consider are normal forces or pressures acting perpendicular to the surface of the control volume.
Examples & Analogies
Think of a calm swimming pool. When no one is moving in the water, the pressure you feel at any point in the water (like at the bottom of the pool) is only due to the weight of the water above you, not due to any movement or waves, similar to how pressure acts in a fluid at rest.
Pressure Distribution Due to Gravity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
At that point, the gravity force is acting it which is the body force component. The gravity force what will be there? It will be, ρgV. So we can have a two force components. One is the surface force component and other is body force. The body force components if you look it that it will be unit weight multiply the volume of the control volume, which is l_x.l_y.l_z.
Detailed Explanation
In a control volume with fluid at rest, we can identify two types of forces acting on it: surface forces (due to pressure) and body forces (due to gravity). The body force is calculated by multiplying the unit weight of the fluid by the volume of the control volume. This highlights how gravity influences the fluid and consequently the pressure distribution within it. Further, the unit weight is represented as the product of the fluid's density (ρ) and the acceleration due to gravity (g).
Examples & Analogies
Imagine a glass filled with water. The water exerts pressure on the bottom of the glass due to both the weight of the water above it and the atmospheric pressure exerted downwards. Similarly, in a tank of water, the deeper you go, the more weight of the water there is above you, leading to an increased pressure at lower depths.
Pressure is Constant on Horizontal Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that we can have a linear variation of pressure from these free surface to this one and that what we get it here the linear variations of the pressure and you can look it that what is a unit weight into the z value. So these are very simple way. The pressure will vary, this is the free surface. At this point the pressure will be the atmospheric pressure, which most often we neglected that which is very less as compared to the liquid what we have generally we consider it.
Detailed Explanation
When analyzing pressures in a fluid at rest, we discover that pressure remains constant along any horizontal plane. This invention arises from the fact that all horizontal points in a fluid are subject solely to the pressure from the fluid column above them. Consequently, as long as the fluid is at rest and not in motion, the pressure at any given horizontal level is uniform throughout. On the other hand, as we move vertically downward in the fluid, the pressure will increase linearly due to the weight of the fluid column above.
Examples & Analogies
Consider the example of a water bottle. If you open the bottle, the pressure at any point on the surface of the water is the same, whether you are measuring at the top, middle, or bottom of the bottle. However, if you were to measure the pressure at various depths, you'd find that it increases deeper you go due to the greater weight of the water above.
The Role of Gauge Pressure and Atmospheric Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The point is what we are going to discuss is that gauge pressure and vacuum pressure. Components now is coming it what is your datum to measure the pressure. Whether you have to make a absolute zero pressure, that means you have a vacuum. From there you are measuring the pressure, or you consider as local atmosphere, to measure the pressure.
Detailed Explanation
In measuring pressure, we consider two types - gauge pressure and absolute pressure. Gauge pressure measures pressure relative to local atmospheric pressure, meaning it considers the surrounding atmospheric pressure as zero. On the other hand, if we measure from a vacuum reference point, that's the absolute pressure. When calculating pressures in practical scenarios, we often consider atmospheric pressure as a reference because most systems operate in atmospheric conditions.
Examples & Analogies
Think of a bicycle tire gauge. When you check the pressure in your tire, it shows the pressure above atmospheric pressure—this is gauge pressure. If the gauge said your tire is at 30 psi, it means the tire pressure is 30 psi more than the atmospheric pressure surrounding it.
Pressure Distribution Dynamics: Hydrostatics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now as we derive pressure distribution equations which in vector forms and let we simplify that equations which earlier we consider the acceleration due to gravity is a vector which will have, and then if you align the gravity in one of the coordinate axis most times that we do along the z directions.
Detailed Explanation
When deriving pressure distribution equations, we often simplify the equations by aligning the gravitational force with one of the coordinate axes, typically the z-axis, which represents vertical depth. When gravity is aligned with the z-direction, we have a consistent framework to analyze how pressure varies with depth in the fluid. Thus, the gradients of pressure can be easily calculated, leading us to understand the behavior of pressure at various depths within the fluid.
Examples & Analogies
Imagine a swimming pool where the depth of the water influences the pressure felt by someone diving into the pool. The deeper you go, the more pressure you experience, which is directly attributable to the weight of the water above you. This analogy reflects how pressure varies with depth in a static fluid.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pressure Variation: Pressure varies only in the vertical direction due to gravity in fluids at rest.
-
Hydrostatic Pressure Equation: The equation P = ρgz is used to calculate the pressure at a specific depth in a fluid.
-
Gauge vs. Vacuum Pressure: Gauge pressure indicates pressure above atmospheric levels, while vacuum pressure indicates below atmospheric levels.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of pressure measurement is a tire gauge, which measures the pressure above the atmospheric pressure inside the tire.
-
In hydrostatic conditions, if a column of water is 5 meters tall, the pressure at the base can be calculated as P = 1000 kg/m³ * 9.81 m/s² * 5 m.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure below, pressure above, in static fluids, it’s all love.
📖 Fascinating Stories
-
Imagine a calm lake; the water's surface is flat. No rush, no flow, just the stillness that keeps the pressure even from its depths to its height!
🧠 Other Memory Gems
-
PLUG - Pressure Lifts Under Gravity, reminding us pressure increases with depth in fluids.
🎯 Super Acronyms
GAP - Gauge Above Pressure, emphasizing that gauge pressure is always above atmospheric pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest due to the weight of the fluid above it.
-
Term: Gauge Pressure
Definition:
Pressure measured relative to atmospheric pressure; the pressure in an enclosed system minus atmospheric pressure.
-
Term: Vacuum Pressure
Definition:
Pressure that is below atmospheric pressure, indicating a partial vacuum.
-
Term: Hydrostatic Equilibrium
Definition:
The condition wherein the net force acting on a fluid element at rest is zero.