Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Control Volume Concept
Unlock Audio Lesson
Today, we'll explore the concept of a control volume when analyzing the pressure field in fluids. Can anyone explain what we mean by a control volume?
Isn't it a defined region in space where we analyze motion or forces acting on the fluid?
Exactly, great job! In static conditions, we consider the shear stress to be zero. So, what type of stress do we encounter on the fluid’s surface?
Normal stress, which is pressure!
Correct! Pressure, P, acts normal to the surface. It's critical because we derive equations describing how pressure varies with coordinates. Remember, this pressure depends on the volume of the control volume and the forces acting on it.
What kind of forces are we discussing?
Good question! We have surface forces, like pressure, and also body forces, primarily gravity. Do we remember how gravity influences pressure?
Yes! It influences pressure through the weight of the fluid above.
Exactly! As we delve deeper, we'll see how all these elements are interrelated.
Pressure Distribution and Properties
Unlock Audio Lesson
Now let's examine how we mathematically express pressure distribution in fluids. The pressure can be expressed in terms of coordinates, P(x, y, z). Can someone describe what it means to express this using a Taylor series?
It helps us approximate the pressure at various points based on known values!
Right! Using Taylor series, we can approximate pressure at different locations in a control volume based on the central point. We can write it as P at the centroid plus the gradient terms. What do we get when we consider pressure gradients in a sitting fluid?
Pressure only varies vertically, along the z-axis, if the fluid is at rest!
Fantastic! That leads us to the hydrostatic equilibrium equations. Who can recap the key finding about pressure in static fluids?
Pressure increases linearly with depth due to the weight of the fluid above!
Well done! So, pressure at any point in a fluid at rest can be found with the equation P = ρgz, where ρ is density and g is gravitational acceleration.
Differentiating Pressure Measurements
Unlock Audio Lesson
Let's discuss different types of pressure measurements. What’s the difference between gauge pressure and absolute pressure?
Gauge pressure is measured relative to atmospheric pressure, whereas absolute pressure is measured from a perfect vacuum.
Great summary! Gauge pressure measures pressure above atmospheric levels. When might we need to use gauge pressure?
In scenarios like tire or blood pressure measurements!
Excellent! Conversely, can anyone provide an example of when absolute pressure is relevant?
In scientific experiments where atmospheric pressure variations need to be accounted for!
Exactly! It’s crucial to choose the appropriate measurement based on context.
Applications of Pressure Principles
Unlock Audio Lesson
To wrap up, let’s discuss real-world applications of these pressure principles. How do you think this knowledge on pressure fields can be useful?
It helps in designing hydraulic systems, like elevators or cars!
Absolutely! What about in meteorology?
Understanding pressure helps predict weather patterns!
Exactly how pressure variations contribute to weather systems. Lastly, can someone summarize the importance of understanding pressure in fluids?
It's vital for solving engineering problems, conducting experiments, and predicting natural phenomena!
Well said! Understanding the pressure field in fluids plays a critical role in numerous fields and applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores how to compute a pressure field when a fluid is at rest, focusing on the normal stress acting on a control volume and the significance of body forces, specifically gravity. Through the use of Taylor series approximations and gradient equations, the relationships between pressure and coordinates (x, y, z) are established.
Detailed
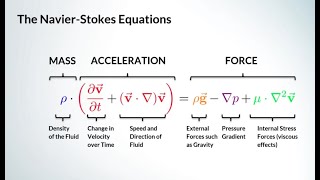
In this section, the pressure field of a stationary fluid is evaluated using the concept of a control volume. When the fluid is at rest, the shear stress on the fluid plane is zero, leading to the conclusion that only the normal stress, equivalent to the pressure, acts on the control surface. The pressure field is denoted as P(x, y, z), where additional forces such as gravity are considered. The body force acting on the control volume is represented as the product of unit weight and the volume of the control volume. Using Pascal's law, it is noted that pressure acts perpendicular to the surface, which leads to the derivation of the pressure distribution through Taylor series approximations. The relationships between these pressures in x, y, and z directions are governed by the hydrostatic equations, establishing that pressure only varies with depth (z-component) in an equilibrium fluid. Gauge pressure and absolute pressure are also discussed, emphasizing how pressure can be measured relative to atmospheric pressure or absolute vacuum conditions. The final formulas clarify how various force components contribute to the total force in static fluid conditions.
Youtube Videos
![Introduction to Velocity Fields [Fluid Mechanics #1]](https://img.youtube.com/vi/CkNo5xGMZS4/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Pressure in a Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if I go for the next ones that how to get the pressure field when fluid is at rest. That means I am just looking the what could be the functions of the P, P = P(x, y, z). If it that it is now again I am considering a very simple case, let us consider a control volume like this okay. This is what my control volume. As I said it when the fluid is at rest the shear stress become zero. So there is no shear stress component on this fluid plane. Only this normal stress which is as equivalent to the pressure will act over this control surface. Over the control surface only the pressure is going to act it because the shear stress is zero okay.
Detailed Explanation
In this chunk, we are introduced to the concept of how pressure behaves in a fluid at rest. When a fluid is not moving, it experiences no shear stress because the fluid layers are not sliding past each other. In this state, the only stress acting on the fluid is normal stress, which equates to pressure. Therefore, the focus is on understanding that pressure is a function of three-dimensional coordinates (x, y, z) and that we can define pressure at any point within a control volume using these coordinates.
Examples & Analogies
Imagine a calm lake. The water is not moving, and if you place a small object beneath the surface, the only force acting on it from the surrounding water is the pressure from the water above it. This pressure is due to the weight of the water and can be thought of as 'weight pushing down' uniformly across the object, which aligns with the idea of normal stress acting in a fluid at rest.
Components of Force in a Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The pressure at the centre of the fluid control volume is assumed to be P(x, y, z). At that point, the gravity force is acting it which is the body force component. The gravity force what will be there? It will be, ρg × V.
Detailed Explanation
This chunk discusses the force components acting within a control volume, focusing on gravity as a body force. Here, 'ρ' represents the fluid density, 'g' is the acceleration due to gravity, and 'V' is the volume of the control volume. Gravity pulls down on the fluid, and we can calculate the body force using the equation ρg multiplied by the volume. This highlights how pressure in a fluid system involves understanding both internal stresses (pressure) and external forces (gravity).
Examples & Analogies
Think of a water bottle filled with water. The weight of the water at the top pushes down on the water at the bottom, creating pressure at the base of the bottle. This pressure can be calculated by considering the weight of the water column, similar to how we quantify the effects of gravity on our control volume.
Pressure as a Function of Coordinates Using Taylor Series
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We need to define now as a pressure as a function of x, y, z is a pressure field what we are looking it. I can use Taylor series to approximate distance of this surface which is far away from it.
Detailed Explanation
In this chunk, the use of the Taylor series to express pressure as a function of coordinates is introduced. The Taylor series is a mathematical tool that allows us to approximate complex functions. By expanding the pressure at a point (x, y, z) using Taylor series, we can derive how pressure changes with distance in three-dimensional space, facilitating a better understanding of the pressure field within the fluid.
Examples & Analogies
Imagine you are on a smooth hill. If you want to know the slope at your feet (the pressure at a specific point), you can use the surrounding terrain to estimate how steep it gets as you move a little further away. This estimation is much like using the Taylor series, where we leverage the known pressure at one point to predict it at another nearby point.
Gradient of Pressure and Force Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I know P(x, y, z) what will be the pressure at this specific point, and if you equate it finally, we will get this one. The gradient and the volume of the control panel. The negative gradient and the volume of control volume is what we will get. This is the force component acting along the y directions.
Detailed Explanation
This segment emphasizes calculating how changes in pressure correspond to changes in gravitational force acting on a control volume. By determining the gradient of pressure (the rate of change of pressure), we can relate it to the force components acting on the fluid. The 'negative gradient' references how pressure decreases the further from the fluid's surface you go, a fundamental concept in hydrostatics.
Examples & Analogies
Picture being in a swimming pool. As you swim deeper, you feel more pressure pressing down on you because of the water above. The change in pressure from the surface to the bottom illustrates how the pressure gradient influences the forces at play in a fluid.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume: A defined space for analyzing fluid forces and motion.
-
Normal Stress: Stress that acts perpendicular to a fluid's surface.
-
Hydrostatic Equilibrium: The condition where fluid pressure changes linearly with depth.
-
Gauge Pressure: The pressure measurement above atmospheric pressure.
-
Absolute Pressure: The pressure measurement based on a perfect vacuum.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When measuring tire pressure, gauge pressure is used to determine how much the tire pressure exceeds atmospheric pressure.
-
Mercury barometers use the concept of hydrostatic pressure to measure atmospheric pressure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure down below, keeps rising as we go, Weight of fluid high, pressure’s never shy!
📖 Fascinating Stories
-
Imagine a deep lake; as you dive deeper, the weight of the water above increases, pushing down and increasing pressure. This story captures how depth influences pressure in a fluid.
🧠 Other Memory Gems
-
P = ρgz: Just remember, 'Rising weight gives pressure, z is where it's at!'
🎯 Super Acronyms
PAB
- Pressure Above Barometer indicates Gauge Pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A defined region in space used to analyze fluid behavior.
-
Term: Normal Stress
Definition:
The stress acting perpendicular to the surface of the fluid.
-
Term: Body Force
Definition:
Forces acting throughout a body, such as gravitational force.
-
Term: Hydrostatic Pressure
Definition:
Pressure exerted by a fluid at rest due to the weight of the fluid above.
-
Term: Gauge Pressure
Definition:
Pressure measured relative to the ambient atmospheric pressure.
-
Term: Absolute Pressure
Definition:
Pressure measured from a perfect vacuum, independent of atmospheric pressure.