Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Pressure in Static Fluids
Unlock Audio Lesson
In static fluids, pressure only acts normally at a surface, and shear stress is zero. Can anyone explain what that means?
It means that there's no force trying to slide the fluid layer across each other, only pressure acts perpendicularly.
Exactly! So, we focus on normal stress, which we denote as pressure. If I ask you to visualize a control volume, what shape comes to mind?
A cube or parallelepiped would be a simple control volume to think about.
Great point! Now, if we consider the pressure at the centroid of this volume, how does gravity play a role here?
Gravity pulls down on the fluid, which increases pressure at lower points in the fluid.
Precisely! This leads us to understanding pressure gradients. In the absence of motion, pressure changes with depth and is a function of the height of the fluid above that point.
Now, let's summarize: pressure increase is linear with depth and is represented mathematically through equations we can derive.
Pressure Functions and Taylor Series
Unlock Audio Lesson
When we represent pressure as a function P(x, y, z), how can we utilize Taylor series for estimation?
We can approximate the pressure at any point using derivatives if we know the pressure at a central point.
Exactly! For small distances, we can say pressure at a nearby point can be expressed as P(x, y, z) + partial derivatives. What does that tell us about higher-dimensional differences in pressure?
It shows how the pressure gradients change in three dimensions. It could lead to complex spatial pressure distributions.
Exactly! Now, remember that we can often neglect higher-order terms for simplicity in basic cases. How does that help us?
It allows us to focus on the key linear effects without complicating the computations unnecessarily.
Well done! So through Taylor series expansions, we derive practical equations for fluid statics.
Gauge Pressure and Vacuum Pressure
Unlock Audio Lesson
Let's talk about how we measure pressure. Who can define gauge pressure?
Gauge pressure is the pressure measured above atmospheric pressure, right?
Correct! And what about vacuum pressure?
Vacuum pressure is measured below atmospheric pressure.
Exactly! The atmospheric pressure acts as a datum for many measurements. Why is this significant?
Using atmospheric pressure helps simplify many physical problems, like determining how fluids behave.
Right! So now we know pressure may vary, but we use methods like barometers that exploit these principles to measure atmospheric pressure. Can someone explain how a mercury barometer works?
It measures pressure by balancing the weight of mercury in a tube against atmospheric pressure.
Great summary! That brings us to the concept of hydrostatic equilibrium and its practical applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on how pressure behaves in a fluid at rest, emphasizing the absence of shear stress and the significance of hydrostatic pressure. It introduces the control volume concept, Taylor series approximations, and distinguishes between gauge and absolute pressures.
Detailed
Detailed Summary
In fluids at rest, the pressure exerted within the fluid can be described by the equilibrium of forces within a control volume. The absence of shear stress means that only normal stresses, equivalent to the pressure, play a role in this context. We consider a simple control volume shaped like a parallelepiped, focused at the centroid where the pressure can be denoted as P(x, y, z).
As gravity acts as a body force within the fluid, deriving pressure at different points becomes essential. The pressure at any given point can be approximated using Taylor series, leading to various forms of pressure equations. The physical implications of these equations reveal that pressure increases linearly with depth due to the weight of the fluid above, influencing points in various Cartesian coordinates.
Furthermore, the section explains the concepts of gauge pressure (measured relative to local atmospheric pressure) and vacuum pressure (measured below atmospheric pressure), with practical implications for measuring pressure using devices like mercury barometers that rely on hydrostatic principles.
This foundation prepares the understanding of fluid mechanics, particularly in contexts where fluid static situations prevail.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Pressure in a Resting Fluid
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
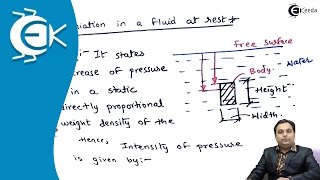
Now if I go for the next ones that how to get the pressure field when fluid is at the rest. That means I am just looking at what could be the functions of the P, P = P (x, y, z). If it that it is now again I am considering a very simple case, let us consider a control volume like this okay. This is what my control volume. As I said when the fluid is at rest the shear stress becomes zero. So there is no shear stress component on this fluid plane.
Detailed Explanation
When a fluid is at rest, its pressure distribution can be defined as a function of its coordinates, represented by P(x, y, z). In a theoretical scenario, we consider a control volume — a fixed space within the fluid — where we analyze how pressure operates. With fluid at rest, the shear stress (a stress that occurs due to the movement of fluid layers sliding past each other) is zero. Therefore, only normal stress, which is equivalent to pressure, acts on the surfaces of this control volume.
Examples & Analogies
Imagine a book lying flat on a table. The weight of the book presses straight down on the table without any sliding or movement. This is similar to how pressure acts in a resting fluid, where only 'downward' pressure is experienced without any forces trying to cause a flow or movement.
Components of Pressure in Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Only this normal stress which is as equivalent to the pressure will act over this control surface. Over the control surface only the pressure is going to act it because the shear stress is zero okay. The pressure at the center of the fluid control volume is assumed to be P (x, y, z). At that point, the gravity force is acting which is the body force component.
Detailed Explanation
Since the fluid is not moving, the only kind of force being considered in our control volume analysis is the pressure acting at the surfaces, along with the gravitational force acting within the fluid's volume. The pressure at the center of our control volume is a function of its spatial coordinates, P(x, y, z). Additionally, we also consider the weight of the fluid above this point, which contributes to the total pressure due to the gravitational effect on the fluid.
Examples & Analogies
Think about the fluid in a large swimming pool. The water exerts pressure down on deeper layers due to both the weight of the water above and the fact that it’s not moving at all—just like how gravity pulls down on everything. The deeper you go, the more pressure you feel, just like you would feel more weight if you had several people standing on your shoulders.
Pressure Components and Body Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The body force components if you look at it that it will be unit weight multiplied by the volume of the control volume, which is simple things. The volume is this much and the unit is where the density and g stands for accelerations due to gravity.
Detailed Explanation
Body forces in a fluid arise due to the weight of the fluid itself acting throughout its volume. This can be calculated by multiplying the specific weight (density times gravitational acceleration) by the volume of the control volume. This relationship helps determine how pressure varies with depth, as the deeper layers support the weight of the layers above them.
Examples & Analogies
If you have a tall glass of water, the pressure at the bottom of the glass is greater than at the top because of all the water above it pressing down. The body force due to gravity is what causes this increased pressure at greater depths.
Pressure and Equilibrium in Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look over this control volume, all these pressures are going to act as Pascal's law says that pressure acts normal to the surface. So we can consider pressures act there normal to the surface. Then we need to define now as a pressure as x, y, z is a pressure field which we are looking at which is a function of x, y, z.
Detailed Explanation
According to Pascal's law, fluid pressure is exerted equally in all directions when contained. Each point in the fluid reacts to pressures in its local environment, resulting in a pressure field that is consistent in any horizontal layer if the fluid is at rest. This field can be described mathematically as a function of spatial coordinates x, y, z.
Examples & Analogies
Consider a sealed balloon. If you were to squeeze one side, you would feel the pressure distribute evenly throughout the balloon. This is similar to how pressure in a resting fluid adjusts evenly across a horizontal layer.
Understanding Pressure Variations Using Taylor Series
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
I can use Taylor series to approximate distance of this surface which is far away from. The pressure at point on the surface can be expressed as ...
Detailed Explanation
Using a Taylor series expansion helps in predicting or approximating how pressure varies in the fluid as you move from one point to another. As the pressure values change across the fluid, this mathematical tool allows us to model and understand those variations more precisely, particularly when distances are relatively small.
Examples & Analogies
Imagine climbing a hill. As you ascend, the incline and the landscape may change gently or sharply. If we were to map these changes, we could use a series of smaller steps to ensure we accurately capture the terrain's slopes—similar to how the Taylor series approximation helps us understand small changes in pressure across distances.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pressure Field: Represents how pressure varies within a fluid at rest, influenced primarily by depth.
-
Control Volume Concept: A defined volume in fluid mechanics to analyze pressures and forces.
-
Gauge and Vacuum Pressure: Important distinctions in pressure measurement; gauge above atmospheric pressure and vacuum below.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When measuring the pressure in a water tank, the pressure at the bottom may be significantly greater than at the top due to the weight of the water column above.
-
Using a mercury barometer to measure atmospheric pressure helps understand the concept of hydrostatic equilibrium.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids at rest, pressure is key, it rises with depth, just wait and see!
📖 Fascinating Stories
-
Imagine you're diving deep underwater; each meter down, pressure pushes harder, like a big hand of water weighing down on you, remember, pressure’s due to what’s above too.
🧠 Other Memory Gems
-
To remember gauge vs vacuum, just think: Gauge is above, vacuum is below! G is for Greater, V is for Void!
🎯 Super Acronyms
P-C-G
- Pressure- Control Volume-Gauge (Remember these steps to analyze pressure in fluids!)
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest due to the weight of the fluid above it.
-
Term: Gauge Pressure
Definition:
The pressure measured relative to the surrounding atmospheric pressure.
-
Term: Vacuum Pressure
Definition:
The pressure measured below the atmospheric pressure.
-
Term: Control Volume
Definition:
A defined volume in terms of spatial boundaries used to analyze fluid behavior.
-
Term: Taylor Series
Definition:
An approximation technique in calculus used to express a function as an infinite sum of terms.