Mercury Barometer
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluids at Rest
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To start, let's talk about fluids at rest. Can anyone tell me what happens to shear stress in this scenario?

I think shear stress becomes zero when the fluid is not moving.

Exactly! When fluids are at rest, the only stress acting is normal stress, which we equate to pressure. Can you remember the relationship between pressure and a control volume?

Pressure acts normal to the surface of the control volume.

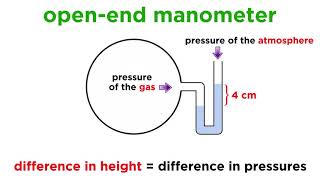
Right! This is crucial for understanding how we measure pressure using devices like the mercury barometer. Let's move on to pressure definitions. What do we mean by gauge pressure?

Isn't it the pressure above atmospheric pressure?

Correct! Gauge pressure is indeed above atmospheric pressure. What's the opposite of that?

That would be vacuum pressure, which is below atmospheric pressure.

Perfect! To recap, in a rest condition, shear stress is zero, and we primarily measure pressure in terms of gauge and vacuum pressure.
Deriving Pressure Distributions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s delve into how we derive pressure variations in a fluid at rest. Can someone summarize our use of the Taylor series approach?

The Taylor series approximates pressure at different points based on its value at a given point in 3D space?

Exactly! This allows us to express pressure changes mathematically. Can anyone illustrate the significance of the hydrostatic equation?

It shows that pressure changes linearly with depth due to gravity!

Great! This linear relationship is vital in understanding how pressure changes with height in a fluid column. If we have a fluid column, what can we say about the pressure at any point?

The pressure at a given depth depends on the height of the fluid column and its density.

Well summarized! So remember, pressure distribution under static conditions is crucial for our mercury barometer. Let’s move to the practical applications next.
Understanding the Mercury Barometer
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

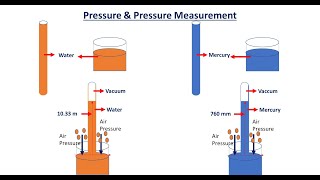
Let's focus on the mercury barometer. Can anyone describe how it works to measure atmospheric pressure?

The barometer uses a column of mercury in a tube. Pressure pushes the mercury up or down based on atmospheric conditions.

Exactly! The height of the mercury column reflects atmospheric pressure. How does altitude affect this measurement?

If you go higher, the atmospheric pressure decreases, which would lower the mercury height!

Correct! This explains why people can feel dizzy at high altitudes, as the pressure is lower. Alright, to conclude this session, can someone summarize the main principles we discussed regarding the mercury barometer?

We learned it measures atmospheric pressure using the weight of mercury and how altitude influences pressure readings.

Perfect! Remember, the mercury barometer is a critical device for understanding atmospheric conditions. Great job today!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section outlines how mercury barometers function in measuring atmospheric pressure through the use of hydrostatic principles. It elaborates on the definitions of gauge and vacuum pressures, the behavior of pressure in a static fluid, and the Taylor series approximations applied in deriving pressure equations. Additionally, it emphasizes the importance of understanding pressure measurements, especially in different environmental contexts.
Detailed
Detailed Summary
In this section, we explore the functioning of the mercury barometer as a tool for measuring atmospheric pressure. The barometer operates based on hydrostatic principles, where the height of a column of mercury in a tube is directly proportional to the atmospheric pressure exerted upon it. The text begins with a discussion on the characteristics of fluids at rest, highlighting that shear stress is zero and only normal stress, equivalent to pressure, acts on the control surfaces. It then introduces the concepts of gauge pressure (pressure above atmospheric) and vacuum pressure (pressure below atmospheric), establishing how gauge pressure is measured relative to the surrounding atmospheric pressure.
The section also covers the theoretical derivation of pressure distributions using Taylor series and emphasizes the simplifications made for practical applications. Specific attention is given to the relationship between pressure variation and gravity, with the section explaining that under static conditions, pressure changes linearly with depth in a fluid.
Finally, the mercury barometer is presented as a classic example of these principles in action—where the measurement of atmospheric pressure is made practical by addressing variations due to altitude and environmental influences, ultimately showcasing the relevance of pressure measurements in real-world applications.
Youtube Videos



![Barometric Pressure [Fluid Mechanics]](https://img.youtube.com/vi/mrrqT4M1X4Q/mqdefault.jpg)




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition and Function of Pressure Measurement
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now as we derive pressure distribution equations which in vector forms and let we simplify that equations which earlier we consider the acceleration due to gravity is a vector which will have a three equations. One will be the z direction, another will be the y direction, another will be the x direction. As we know it we measure the atmospheric pressure and the different and that what we can use this mercury barometer.
Detailed Explanation
This chunk discusses the basic principle behind measuring pressure using barometers like the mercury barometer. The pressure in any fluid can be described mathematically by equations that include components in several directions (x, y, and z). The gravitational force acts in the vertical direction (z), while pressure acts uniformly across horizontal planes. This helps us understand how pressure changes with height in the atmosphere and can be measured using instruments like barometers.
Examples & Analogies
Think of a tube filled with mercury. As the atmospheric pressure pushes down on the mercury in a reservoir, it forces the mercury up the tube. The height of the mercury in the tube indicates the atmospheric pressure. Just like how a water balloon feels tighter when you squish it, the pressure of the air pushes down on the mercury, causing it to rise.
Measurement of Atmospheric Pressure
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
But if you most of the case as you know it when you consider the fluid all the fluid will have a surrounding of a part of atmosphere. Most of the cases what we consider here, we are not solving the problems in a space or area. We are just solving or any other planets, we are just solving the very simplified problems in and around the earth.
Detailed Explanation
This chunk explains the significance of measuring atmospheric pressure at various altitudes, particularly in Earth’s atmosphere. Air pressure decreases with elevation, which is essential for understanding weather patterns and altitude sickness. Mercury barometers are commonly used to measure this pressure, capturing the effects of atmospheric variations. The reading on the barometer gives us the local atmospheric pressure, which changes depending on where you are relative to sea level.
Examples & Analogies
Imagine climbing a mountain. As you rise, the air gets thinner, and you begin to feel dizzy. This is because the atmospheric pressure decreases with altitude, just as the mercury in a barometer tube would drop if you moved to a higher location. Understanding this helps climbers prepare better for high-altitude conditions.
Mechanics of the Mercury Barometer
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now the point is what we are going to discuss is that gauge pressure and vacuum pressure. Components now is coming it what is your datum to measure the pressure. Whether you have to make a absolute zero pressure, that means you have a vacuum...
Detailed Explanation
This section describes two types of pressures measured using a mercury barometer: gauge pressure, which is the pressure relative to the atmospheric pressure, and vacuum pressure, which measures pressure in a vacuum (absolute pressure). A mercury barometer uses the height of mercury to tell us the atmospheric pressure at a specific altitude, which is valuable for various scientific and practical applications.
Examples & Analogies
When you take a deep breath, the pressure inside your lungs is higher than the surrounding atmospheric pressure (gauge pressure). Conversely, when you suck air out of a sealed container, the pressure inside decreases (vacuum pressure). A mercury barometer works on a similar principle — it uses the weight of mercury to show how much atmospheric pressure is resting on it.
Applications and Importance of the Mercury Barometer
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
With this note let me summarize today lecture that we started with the examples of gravity dam and liquid working as a rigid body motions which we will discuss much later more that...
Detailed Explanation
This concluding section emphasizes the importance of the mercury barometer in measuring atmospheric pressure. It can be used for weather predictions and understanding environmental changes. The lecture wraps up by reiterating the need to comprehend various pressures and their effects in different environmental conditions.
Examples & Analogies
Meteorologists rely heavily on mercury barometers to take accurate measurements of atmospheric pressure, which help them forecast weather accurately. Just like how you might regularly check the temperature before leaving the house, keeping an eye on atmospheric pressure can tell you whether a storm is likely to come your way.
Key Concepts
-
Fluids at Rest: Shear stress is zero; only normal stress (pressure) acts on fluid surfaces.
-
Gauge vs. Vacuum Pressure: Gauge pressure is above atmospheric; vacuum pressure is below it.
-
Hydrostatic Pressure Principle: Pressure varies linearly with depth in a fluid column.
-
Mercury Barometer Functionality: Utilizes mercury column height to measure atmospheric pressure.
Examples & Applications
Example 1: A mercury barometer at sea level typically shows a reading of about 760 mm Hg, corresponding to 101.3 kPa of atmospheric pressure.
Example 2: Climbing Mount Everest, the mercury barometer will show a significantly lower pressure due to the high altitude, indicating a reduction in atmospheric pressure.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Pressure in air, oh so fair, gauge it high or low with care!
Stories
Imagine a brave explorer climbing a mountain. Each step up makes the air thinner, and with less pressure, the mercury barometer drops, showing how high they've climbed, a reminder to breathe slowly!
Memory Tools
GVP for pressure: Gauge, Vacuum, and the importance of Measurement!
Acronyms
Use G for Gauge, V for Vacuum, and M for Measurement, together they spell out GVM to remind you of pressure concepts!
Flash Cards
Glossary
- Gauge Pressure
The pressure measured relative to ambient atmospheric pressure.
- Vacuum Pressure
The pressure measured below atmospheric pressure.
- Mercury Barometer
An instrument that measures atmospheric pressure utilizing a column of mercury.
- Hydrostatic Pressure
The pressure exerted by a fluid at equilibrium due to the force of gravity.
- Control Volume
A defined volume in fluid mechanics within which mass and energy balances are applied.
Reference links
Supplementary resources to enhance your learning experience.
