Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Conservation
Unlock Audio Lesson
Today, we'll be exploring the fundamental concept of mass conservation in fluid flow. Can anyone tell me what mass conservation means?
Does it mean that mass can't be created or destroyed in a closed system?
Exactly! This principle states that the mass flow rate in and out of a control volume must balance. How do we express this mathematically?
Is it something like inflow equals outflow?
"Right! For incompressible flow, we simplify it to
Applying Momentum Equations
Unlock Audio Lesson
Now that we know about mass conservation, let’s consider momentum equations. What do we use momentum equations for in fluid dynamics?
To determine how forces from fluid flows influence structures or objects?
Precisely! We apply the Reynolds transport theorem to find the change in momentum flux. Can anyone share the general form of the momentum conservation equation?
It’s the sum of forces equals the change in momentum.
Correct! It’s crucial for computing what happens in a control volume when a jet strikes a surface.
Example of Force Calculation
Unlock Audio Lesson
Let's apply these concepts. Imagine a water jet hitting a plate. If our jet has a velocity of 20 m/s and the plate moves at 15 m/s, how do we find the net force acting on this system?
We should compare the momentum influx due to the jet and the momentum outflux since the plate will affect the water's direction.
Excellent thinking! This will allow us to find the force contribution in the x-direction. Remember, relative velocities are vital here.
So, we need to also consider how the jet splits and changes direction?
Yes! Direction change directly affects the momentum calculation.
Control Volume Analysis
Unlock Audio Lesson
Next, let's discuss control volumes. Why do we focus on fixed versus moving control volumes in our analyses?
A fixed control volume keeps the boundaries constant, which simplifies calculations.
Exactly! However, for moving conditions, we have to adjust calculations for the motion of the control volume, like factoring in velocities. What assumptions are necessary for these problems?
We often neglect gravity or viscous forces to simplify the problem.
Correct! These assumptions are standard, especially when analyzing jet flow interactions.
Final Calculation Example
Unlock Audio Lesson
Let’s summarize with an example of a jet striking a vane. If we know the flow area and velocity, how do we find the force to hold the vane stationary?
We’d use mass conservation first to find the mass flow rate, then apply momentum equations!
Great, and remember to consider the angle the jet makes with the vane as it changes the force component needed.
We need to ensure we account for both x and y components of the force.
Precisely! Always break forces into components for clarity.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Anchoring force calculation involves deriving equations based on mass conservation and momentum flux. It examines incompressible fluid dynamics, particularly in scenarios such as jets impinging on surfaces and evaluating forces acting due to the flow. Key examples illustrate how to calculate forces acting on moving control volumes.
Detailed
Anchoring Force Calculation
This section delves into the principles and calculations involved in determining anchoring forces in fluid dynamics. It begins with the application of the mass conservation equation, emphasizing the relationship between inflow and outflow in an incompressible flow scenario. Using Reynolds transport theorem, the section focuses on momentum flux and the net change within control volumes.
The section outlines how to compute various force components resulting from fluid interactions, specifically when jets impinge on stationary or moving surfaces, emphasizing the balance of momentum and the impact of pressure forces. Importantly, it introduces the concept of working under steady flow conditions to simplify calculations. Several practical examples, such as calculating the force on a vane or on a moving plate in contact with a water jet, are presented, illustrating the application of these concepts in real-world scenarios. Throughout, critical assumptions like neglecting gravitational effects or viscous forces are made to streamline the analysis.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Conservation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
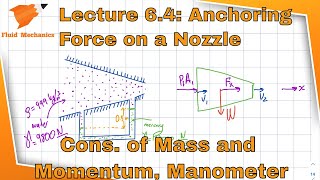
Now let us apply the mass conservation equation where is inflow minus outflow and this case will be,
Outflow = Inflow.
This is what the discharge is given to us, the volumetric discharge is given to us divide by the area will get it the velocity, that the velocity part what we have.
Detailed Explanation
The mass conservation equation states that the amount of mass flowing into a system (inflow) must equal the amount of mass flowing out of the system (outflow) over a certain time period. In this context, we can express it mathematically as 'Outflow = Inflow.' To find the velocity of the fluid, we can use the volumetric discharge divided by the cross-sectional area of flow. This is essential for determining how fast the fluid moves as it enters or exits a control volume.
Examples & Analogies
Imagine a garden hose. The water flowing into the hose (inflow) must equal the water coming out of the hose (outflow) as long as there are no leaks. If you know how much water is being released per second (volumetric discharge) and the size of the hose (area), you can easily find out how quickly the water is flowing.
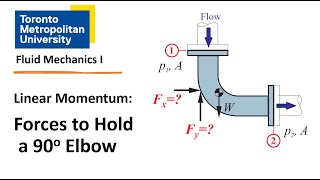
Force Acting in X and Y Directions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we have to find out what is the force acting in R and the R directions, we have the pressure component here. Applying this Reynolds transport theorems and the simplifying the tops. Here, this is the main concept what we have considered that there is a change of the momentum flux within the control volume.
Detailed Explanation
To determine the forces acting on a system, we analyze the components of force in both the x-direction and the y-direction. The pressure acting within the control volume contributes to these forces. By applying Reynolds Transport Theorem, we can simplify the changes in momentum flux, which is crucial for understanding how forces interact within the system and how they relate to fluid flow.
Examples & Analogies
Think about riding a bike against a strong wind. The air exerts pressure on you, pushing you backward (force in the x-direction). If you want to maintain your speed, you need to pedal harder to counter that force. Similarly, calculating the forces in our fluid system helps us understand how to maintain motion despite the acting pressures.
Momentum Flux Changes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Neglecting even though flow is technically unsteady, making it the problems in a steady nature. Then we have two momentum flux components, one is influx another is outflux, applying the momentum flux in x direction, the pressure into the area and that what I will get it and in terms of value, I will get it 355 approximately Newton.
Detailed Explanation
In fluid dynamics, momentum flux is the momentum per unit area flowing through a system. Even if flows are technically unsteady, simplifications can be made to treat them as steady for ease of calculation. We consider two components: influx (momentum entering the system) and outflux (momentum exiting the system). By applying the momentum flux in the x-direction (width of the exit area), we can calculate the net force acting on the system, which in this case, is approximately 355 Newton.
Examples & Analogies
Imagine water rushing into a full bathtub (influx) while some of it is draining out (outflux). The momentum of the incoming water relates to how quickly it pushes against the existing water in the tub—this is similar to analyzing forces in our fluid control volume.
Water Jet Example
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
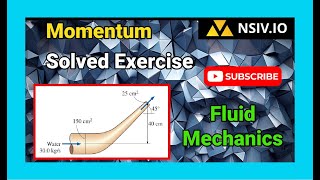
Now take another example: a water jet impinging normal to a flat plate that moves to the right at velocity Vc. Find the force required to keep the plate moving at a constant velocity if the jet density is 1000 kg/m³, the jet area is 3 cm², and Vj and Vc are respectively 20 and 15 m/s.
Detailed Explanation
In this example, a water jet strikes a flat plate while the plate moves at a constant speed. We need to find the force required to keep the plate moving at that speed. We know the density of the jet (1000 kg/m³) and the areas and velocities of both the jet and the plate. Understanding the balance of forces acting on the plate due to the momentum of the jet will allow us to calculate the necessary thrust to maintain constant velocity.
Examples & Analogies
This situation can be likened to a person trying to hold a piece of cardboard against a strong wind. The wind exerts force on the cardboard (like the water jet), and the person must apply enough force to keep the cardboard steady and moving along with the wind.
Applying Momentum Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we apply the momentum conservation equations to compute what will be the force. First, again steady flow conditions which is standard assumptions, and applying RTT.
Detailed Explanation
Applying momentum conservation allows us to link the mass flow rates and velocities to the forces acting on an object in a fluid flow scenario. Using the Reynolds Transport Theorem (RTT), we can formulate equations that help quantify these forces based on the changes in the momentum of the fluid as it interacts with the moving plate.
Examples & Analogies
Imagine a constant flow of air from a fan directed at a wind turbine. As the air moves through the turbine, it transfers momentum to the turbine's blades, causing it to turn. By analyzing this momentum change, we determine the forces in action that allow the turbine to convert wind energy into electrical energy.
Deceleration and Landing of Spacecraft
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us have an interesting example of decelerating the spacecraft before landing on Earth. A spacecraft with a mass of 15,000 kg dropping vertically at a constant speed of 600 m/s fires its rocket to slow down.
Detailed Explanation
In this example, we're considering the landing of a spacecraft, which requires deceleration to safely reach the ground. It does this by firing rockets to counteract its velocity. The calculations involve determining the thrust exerted by the rocket engines and how this affects the spacecraft's motion. The conservation of momentum here plays a crucial role in calculating the required force and resulting deceleration.
Examples & Analogies
Think about a car approaching a red traffic light at high speed. To stop safely, the driver applies the brakes, which exert a force in the opposite direction of the car's motion. Similarly, the spacecraft's rockets must generate sufficient force to reduce its speed for a safe landing.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Incompressible Flow: A type of flow where the fluid density remains constant.
-
Mass Balance: The idea that mass entering a control volume equals mass exiting it.
-
Momentum Conservation: A principle stating that the total momentum remains constant unless acted upon by external forces.
-
Control Volume: A defined volume to analyze the flow and forces acting on it.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Calculating the anchoring force acting on a plate being hit by a water jet.
-
Example 2: Evaluating the forces on a vane struck by a jet at an angle.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mass stays the same, come what may; in and out, it’s here to stay.
📖 Fascinating Stories
-
Imagine a river flowing into a pool. If nothing leaks out, the water level stays stable; that's mass conservation in action.
🧠 Other Memory Gems
-
MOM: 'Mass Out = Mass In' helps remember mass conservation for every fluid system.
🎯 Super Acronyms
MOM - Mass Out = Mass In ensuring accounting for flow.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Conservation
Definition:
The principle stating that mass in a closed system cannot be created or destroyed.
-
Term: Momentum Flux
Definition:
The rate of transfer of momentum through a given area.
-
Term: Control Volume
Definition:
A fixed or moving volume in which fluid flow is analyzed.
-
Term: Reynolds Transport Theorem (RTT)
Definition:
A mathematical theorem used to relate the rate of change of a system to fluxes across its boundaries.
-
Term: Impulse
Definition:
The change in momentum resulting from a force applied over a period of time.