Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Conservation
Unlock Audio Lesson
Today, we're going to delve into the concept of mass conservation as it applies to fluid dynamics. Can anyone tell me what we mean by mass conservation in this context?
Is it that mass cannot be created or destroyed in a closed system?
Exactly! In fluid dynamics, this leads us to state that the mass influx must equal the mass outflux when we are examining a control volume. This is expressed mathematically as Outflow = Inflow.
How does this apply when dealing with incompressible flow?
Great question! For incompressible flow, the density remains constant, simplifying our calculations. We can use the continuity equation, which states that the mass flow rate is constant across any cross-section.
Can you give an example of how we might use this principle in a real-life scenario?
Sure! Imagine a horizontal jet of water striking a vane. Here, we can calculate the mass flow rate at the inlet and the outlet, applying the principles we've just covered.
To summarize, the principle of mass conservation helps us ensure that all fluid entering a control volume exits it, which is foundational when we analyze fluid motion.
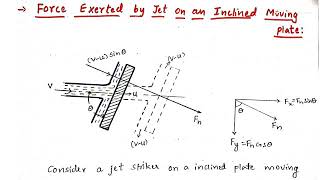
Calculating Forces on the Vane
Unlock Audio Lesson
Now that we understand mass conservation, let's talk about calculating the forces acting on the vane when hit by a jet. How can we estimate these forces?
Do we need to consider the momentum flux?
Exactly! By applying the Reynolds transport theorem, we can relate the change of momentum flux within our control volume to the forces acting on it. What factors do we need to consider in our calculation?
We need to factor in the velocities of both the jet and the moving plate.
Correct! So when the jet strikes the vane, we also need to account for the velocity at which the plate is moving. If the jet density is also provided, we can compute the required force to keep the plate moving at a constant velocity.
Could you walk us through solving a specific example?
Of course! Let's say we have a jet with a density of 1000 kg/m³, an area of 3 cm², and velocities of 20 m/s for the jet and 15 m/s for the plate. We can use these values to determine the force required.
In summary, the forces on a vane due to a jet can be calculated using the principles of momentum conservation and taking into account the relative velocities.
Examples and Applications
Unlock Audio Lesson
We've talked about the theory; now let's look at a couple of examples to make these concepts clear.
What’s the first example we’re going to tackle?
We'll start with the horizontal jet striking a flat plate. Given the dimensions and velocities we've just mentioned, how would we proceed?
I think we should first calculate the mass flow rate, then determine the force based on momentum change.
Exactly! By determining the mass flow rate, we can derive the necessary force exerted on the vane. Remember, neglecting external factors like gravity simplifies our calculations.
What if we increase the angle of the vane? Would that change our calculations?
Good observation! Changing the angle affects how the jet distributes its momentum among the upward and downward directions. We need to reevaluate the force in those cases.
In this session, we've effectively used our examples to illustrate how theoretical concepts apply to real-world fluid dynamics problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on mass conservation in fluid flow, the calculation of forces acting on a vane due to jet impingement, and introduces Reynolds transport theorem to understand changes in momentum within a control volume.
Detailed
In this section, we explore the interaction of a horizontal jet striking a vane. We start by applying the mass conservation equation, establishing that outflow equals inflow in incompressible flow conditions. We also discuss the calculation of velocity from volumetric discharge and the forces acting on the vane. Through Reynolds transport theorem, we analyze the change of momentum flux within a chosen control volume. The section further explains how to compute the force acting on the vane when a water jet is directed at it, considering additional complexities such as the vane's movement and jet splitting into two equal directions when it strikes the vane. Finally, we explore example problems to enhance our understanding, making pivotal connections between theoretical concepts and real-world applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Conservation in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us apply the mass conservation equation where is inflow minus outflow and this case will be,
Outflow = Inflow.
Incompressible flow, \(\rho_1A_1V_1 = \rho_2A_2V_2\)
Detailed Explanation
In fluid mechanics, the principle of mass conservation states that the mass flow rate must remain constant between any two points in a flow system. In this case, we equate the mass inflow to the mass outflow. The equation represents incompressible flow where the density (\(\rho\)) remains constant. The formula \(\rho_1A_1V_1 = \rho_2A_2V_2\) means that the product of cross-sectional area (A) and velocity (V), multiplied by density, must be equal for both incoming and outgoing fluid at two different sections.
Examples & Analogies
Imagine water flowing through a garden hose. If the hose narrows at one end, the flow speed must increase to maintain the same volume of water passing through per second. This is similar to how mass flow conservation applies in our equation.
Applying Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
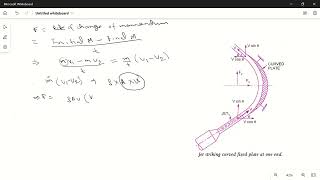
Now we have to find out what is the force acting in the x and y directions, the pressure component here. Applying Reynolds Transport Theorems and simplifying the calculations, the change of the momentum flux within the control volume becomes significant in relation to the momentum thrust from the fluid.
Detailed Explanation
Reynolds Transport Theorem (RTT) is a mathematical framework that helps us relate the flow of mass and momentum in a control volume. In this context, we analyze the forces acting on the vane due to the fluid jet. The theorem helps simplify complex variables by focusing on the momentum flux, determining how the momentum changes as fluid flows through the control volume. This is essential to understanding the forces on the vane due to the jet's momentum.
Examples & Analogies
Consider a car moving through a tunnel. The way air is pushed out of the tunnel by the moving car can be likened to momentum being transferred. If the car suddenly stops, the change in air momentum can create a pressure wave. Similarly, fluid jets impart force through velocity and pressure changes.
Calculating Forces from Fluid Interaction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To compute the force applied by the fluid jet on the vane, we first determine the momentum flux and then apply the momentum conservation equation. This yields a force acting in the x-direction of approximately 355 Newtons.
Detailed Explanation
After analyzing the momentum flux, we determine the force exerted on the vane. We calculate the momentum change using the momentum conservation equation, which states that the net external force acting on a control volume equals the rate of change of momentum within that volume. In our case, we derive a force value based on the fluid's momentum interactions, specifically identifying 355 Newtons as the resulting force acting in the x-direction.
Examples & Analogies
Picture a basketball player pushing against a wall. The harder they push (or the faster they throw the ball), the stronger the force exerted on the wall. Similarly, a fluid jet's momentum transfer reflects how force is generated through its mass and velocity.
Example Problem: Water Jet and Moving Plate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us consider a water jet impinging on a flat plate moving to the right at velocity Vc. The water jet's density is 1000 kg/m³, its area is given, and we must find the force necessary to maintain the plate's constant velocity.
Detailed Explanation
In this scenario, the water jet impacts a moving plate, resulting in an interaction where we need to compute the force to offset the momentum transfer from the water. By applying mass and momentum conservation, and using known variables like density, velocity, and area of the jet, we calculate the force that keeps the plate moving at a constant speed, despite the opposing forces from the jet.
Examples & Analogies
Think of a leaf blower aimed at leaves lying on the ground. While blowing leaves, the force of the air pushes against the leaves. If the blower moves forward, similar to the plate, a balance of force needs to be managed to keep it moving steadily while still applying force to the leaves.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Conservation: The principle that mass is conserved in a closed system, leading to inflow equaling outflow.
-
Incompressible Flow: A type of fluid flow where density does not change.
-
Reynolds Transport Theorem: A theorem for relating fluid properties in a control volume to understand momentum changes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating the force on a vane when a water jet strikes it at a certain velocity.
-
Determining the changes in momentum flux when varying the angle of the vane.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flow and go, the mass must show; what comes in must come out, that's how we know!
📖 Fascinating Stories
-
Imagine a river flowing into a lake. The water that enters must equal what flows out, demonstrating mass conservation.
🧠 Other Memory Gems
-
I.C.E.: Incompressible, Conservation, Equilibrium—think of these when dealing with fluids!
🎯 Super Acronyms
M.I.R.
- Momentum In-Rate—this helps remember how momentum behaves at the control surface.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Conservation
Definition:
Principle stating that mass cannot be created or destroyed in a closed system; inflow equals outflow in fluid dynamics.
-
Term: Incompressible Flow
Definition:
A type of fluid flow where the density remains constant throughout the flow.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem in fluid mechanics that relates the rate of change of momentum within a control volume to the inflow and outflow across its boundaries.
-
Term: Momentum Flux
Definition:
The rate of transfer of momentum through a unit area per unit time.
-
Term: Control Volume
Definition:
A defined region in space used to analyze fluid flow and apply conservation laws.