Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Mass Conservation and Inflow/Outflow
Unlock Audio Lesson
Today, we'll explore the mass conservation equation. Can anyone tell me what it means when we say outflow equals inflow in fluid dynamics?
Does it mean that the fluid entering a system is equal to what leaves it?
Exactly! This is essential for balancing systems in incompressible fluids. Let’s remember the acronym 'IEO' for Inflow Equals Outflow. Moving on, we derive velocity from volumetric discharge divided by area. Can you relate that to an example?
If we have a jet with a certain area and velocity, we can calculate flood impacts in channels!
Nice connection! How would you compute the velocity using the discharge and area?
By dividing discharge by cross-sectional area.
Great! Understanding this will be vital as we study momentum flux.
To sum up, we learned that inflow equals outflow is crucial for fluid systems and can directly help us calculate velocity where necessary.
Reynolds Transport Theorem Application
Unlock Audio Lesson
Today, we’ll delve deeper into the Reynolds Transport Theorem. What role does it play in our calculations?
It helps us relate the change in momentum of a fluid within a control volume to the forces acting on it.
Exactly! We can find forces acting in both x and y directions using RTT. Can anyone summarize the main components it comprises?
It includes mass flow rates, velocities, and pressure distributions within an area.
Right! Let’s remember the mnemonic 'MVP' – Mass, Velocity, Pressure, for RTT. As we apply these equations, why is it significant to compare inflow and outflow?
To elucidate how the control volume behaves under momentum exchanges!
Precisely! This understanding enables us to analyze systems more effectively.
Application Example: Water Jet and Moving Plate
Unlock Audio Lesson
Let’s analyze an example: A water jet striking a flat plate moving at a constant velocity. What do we need to determine the force required to maintain that plate's movement?
We need the velocities of the jet and the plate, as well as the density of the fluid.
Exactly! The force can be calculated using the momentum change from the jet. What happens to forces if we ignore the weight of the jet?
It simplifies our calculations since we maintain steady flow assumptions!
Great point! Working through this example helps visualize how forces interact in fluid dynamics.
In summary, knowing the velocities and density helps determine the necessary force on the plate.
Spacecraft Deceleration Analysis
Unlock Audio Lesson
Let’s wrap up with a fascinating application: How do we decelerate a spacecraft during landing?
By using solid rocket fuels that expel gas to create thrust against gravitational forces?
Correct! We can calculate the thrust using the mass flow rate and the gas velocity. Why is this significant when considering net forces?
Because understanding these forces will help optimize landing strategies!
Precisely! Using the momentum conservation principles, we can state that the thrust needed is essential for altering the spacecraft's velocity effectively.
To summarize, we reviewed how thrust from expelled gases helps control spacecraft descent, highlighting the importance of relative velocities.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concepts of mass conservation and momentum flux are explored through a series of calculations aimed at understanding fluid dynamics, with specific examples such as water jets and spacecraft dynamics. Key equations and principles are established to illustrate the methods used in force and velocity calculations.
Detailed
In fluid dynamics, mass conservation equations play a crucial role in understanding fluid behavior under varying conditions. This section focuses on the concept of incompressible flow, illustrating how inflow equals outflow in a steady state. Through the application of Reynolds Transport Theorem (RTT), students learn how to calculate the forces acting on objects due to the momentum flux in control volumes. Examples include calculating forces on a moving plate impinged by a water jet and analyzing the dynamics of a spacecraft decelerating upon landing. Additionally, the significance of relative velocity, momentum conservation, and pressure distributions are highlighted. Key calculations involve determining velocities based on volumetric discharge and forces exerted by impinging jets, establishing a robust framework for understanding the principles of fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Conservation in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us apply the mass conservation equation where inflow minus outflow and this case will be,
Outflow = Inflow
ρ1A1V1 = ρ2A2V2
This is what the discharge is given to us, the volumetric discharge is given to us divide by the area will get it the velocity, that the velocity part what we have.
Detailed Explanation
In fluid mechanics, the law of conservation of mass states that mass cannot be created or destroyed. When analyzing fluid flow in a pipe or channel, we can equate the mass flow rates at two different cross-sections. This equation states that the mass flow rate of the fluid entering a section of the flow must equal the mass flow rate leaving that section.
Here, ρ represents the fluid density, A the cross-sectional area, and V the velocity. Therefore, if we know the discharge (the amount of fluid flowing per unit time) and the area of the flow, we can find the velocity of the fluid. For example, if the inflow mass must equal outflow, the equation ensures continuity in the flow - no fluid is lost or added in a closed system.
Examples & Analogies
Think of mass conservation like water flowing through a hose. If you have a garden hose of a certain diameter, the water flowing in one end must flow out the other end at the same rate; otherwise, water would either accumulate (like a clog) or decrease (like a vacuum), which doesn't happen. That’s why the cross-sectional areas of the hose and the speed of water flow are directly related.
Force Calculation Using Momentum Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we have to find out what is the force acting in the x and y directions. Applying the Reynolds transport theorem and simplifying the equations, we consider a change in momentum flux within the control volume. If the change is insignificant compared to the momentum thrust coming from the fuel, we set it to zero.
Detailed Explanation
To calculate forces in fluid systems, particularly those involving jet propulsion, we apply the Reynolds transport theorem, which relates the dynamics of the fluid within a control volume to those at the boundaries. In this context, we analyze how the momentum (mass * velocity) of the fluid changes as it enters and exits the control volume. If the forces due to changes in momentum are less significant than those from the fuel's propulsion, we can ignore them for simplicity and focus solely on the thrust generated by the fuel.
Examples & Analogies
Consider a rocket launching. The force needed to push the rocket upwards is primarily provided by the engines pushing downwards. As the rocket accelerates, we can consider the momentary changes in speed irrelevant compared to the overall thrust coming from the engines. This means we just focus on how fast the fuel is expelled to understand how to keep accelerating the rocket.
Example Scenario with Water Jet Impinging on a Plate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
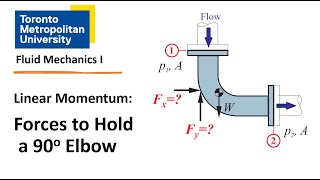
Let’s take a water jet, which impinges normal to a flat plate moving to the right with a velocity Vc. The goal is to find the force required to keep the plate moving at a constant velocity. Given parameters include water density, jet area, and velocities for both the jet and the plate.
Neglecting weights and assuming a steady flow, we apply mass conservation equations.
Detailed Explanation
In this example, we assess the forces acting on a plate as a water jet impacts it. We know the velocities of the jet and the plate, and we use mass and momentum conservation principles to calculate the force needed to maintain the plate’s speed. As the jet strikes the plate, it splits into two equal parts upward and downward. The changes in momentum from the incoming and outgoing jets provide the forces acting on the plate. By applying mass conservation, we find the velocities involved in the water's movements are crucial for calculating the actual forces.
Examples & Analogies
Imagine a car driving into a powerful rainstorm. Each droplet of rain hits the windshield and bounces off; even if the car keeps moving at a steady pace, the force from the raindrops striking the windshield exerts pressure that could push against the car. Similarly, while the water jet hits the plate, it generates an opposing force needing to be countered to keep the plate moving at a constant speed.
Momentum Conservation in Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applying the momentum conservation equation for the control volume, we can compute that inflow equals outflow under steady conditions. Because there are no external forces affecting the system, we can equate the sum of the momentum forces acting on our control volume to zero.
Detailed Explanation
Using the principles of momentum conservation, we find that the amount of momentum entering the control volume is balanced by that exiting it. When we assume the flow is steady and cut out any effects from external forces, we can simplify our calculations by concluding that the total momentum remains constant. This is fundamental in analyzing how systems react when fluid dynamics are involved.
Examples & Analogies
Think about a balance scale with weights on both sides. If you know what is on one side, you can infer what is on the other to keep the scale balanced. The same idea applies here; if you know the forces and velocities of the fluid entering and exiting, you can understand the overall behavior of the system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Conservation: The principle that the mass of fluid entering a system equals the mass leaving it.
-
Reynolds Transport Theorem: A fundamental theorem that relates fluid dynamic quantities within a control volume to the flow across its boundaries.
-
Momentum Flux: The rate of transfer of momentum as fluid flows through certain areas.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating momentum changes resulting from a water jet colliding with a surface.
-
Analyzing how a spacecraft decelerates as it expels gases during landing.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a fluid's flight, mass stays right; inflow and outflow, a balance in sight.
📖 Fascinating Stories
-
Imagine a water jet striking a plate as it travels swiftly. To keep it moving, we calculate the force using momentum, knowing inflow equals outflow.
🧠 Other Memory Gems
-
MVP - Mass, Velocity, Pressure help us remember RTT components easily.
🎯 Super Acronyms
IEO for Inflow Equals Outflow in fluid dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Inflow
Definition:
The movement of fluid into a specified system or volume.
-
Term: Outflow
Definition:
The movement of fluid out of a specified system or volume.
-
Term: Incompressible Flow
Definition:
Flow where the fluid's density remains constant.
-
Term: Momentum Flux
Definition:
The rate of momentum transfer per unit area.
-
Term: Reynolds Transport Theorem (RTT)
Definition:
A mathematical statement that relates the change of momentum in a control volume to the flow of momentum across its boundaries.
-
Term: Control Volume
Definition:
A defined region in space through which fluid flows.
-
Term: Steady Flow
Definition:
A type of fluid flow where the fluid's velocity at a given point does not change over time.