Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Conservation
Unlock Audio Lesson
Today, we will discuss mass conservation in fluid flow. Remember, mass conservation states that the mass entering a control volume must equal the mass exiting it. Can anyone explain what this means, perhaps with an example?
So, if we have a pipe filled with water, the amount of water entering one end must equal the water coming out of the other end, right?
Exactly! This principle is crucial for understanding fluid flows. We often represent this as outflow equals inflow. To remember that, think of 'In = Out'.
What happens if the fluid is incompressible?
Great question! Incompressible fluids don't change density, making mass conservation simpler. You just apply the flow rate directly.
Are there other factors we should consider in real-world applications?
Yes! Always consider things like pressure and velocity, as they can affect flow behavior significantly.
In summary, for incompressible flow, mass conservation helps predict how fluids behave in systems. Think of it as 'In = Out' always!
Momentum Transport in Control Volumes
Unlock Audio Lesson
Now, let’s connect mass conservation to momentum. We will use Reynolds' transport theorem for this. Can anyone recall what momentum flux means?
I think it’s the amount of momentum passing through a certain area?
Correct! It’s crucial to analyze how much momentum a fluid transfers within a control volume. This helps when calculating forces. Who can explain how we might apply this to our earlier water jet example?
If the jet hits a plate, the change in momentum of the jet translates into a force on the plate, right?
Exactly! When the jet strikes the plate, its momentum changes, resulting in a net force that affects the plate. You can visualize it like bouncing a ball; it hits and pushes back.
And how do we calculate that force?
We use the momentum flux difference across the control volume. Always keep in mind the formula for calculating force based on momentum changes—it's powerful!
In summary, recognizing how momentum is transported in a control volume allows us to compute forces effectively.
Practical Example: Water Jet Application
Unlock Audio Lesson
Let’s apply what we learned by analyzing a water jet that strikes a flat plate. What key parameters do we need to consider?
We need to know the density of water, the velocity of the jet, and the area of impact.
Absolutely! These factors will allow us to calculate the impinging force. Remember, we also need to understand if the flow is steady or unsteady.
What if the plate is moving while the jet strikes it?
Good point! In moving conditions, we have to adjust our calculations to account for the relative velocity between the jet and the plate.
Can you summarize how we would set up this type of problem?
Certainly! Define your control volume, establish mass and momentum equations, calculate forces based on the flux differences, and remember to adjust for motion. It’s all about understanding conservation in action!
Applications in Real-World Scenarios
Unlock Audio Lesson
Today we transition from jets to another application—spacecraft deceleration. How does our previous knowledge apply here?
The spacecraft will also experience forces due to change in momentum when rockets fire, right?
Exactly! The thrust created by firing the rocket engines is similar to the water jet example, as it changes the momentum of the spacecraft.
How do we calculate the thrust needed to decelerate the spacecraft?
We determine the change in momentum required over time, using the mass flow of the exhaust gases. Remember to apply the impulse-momentum theorem!
Can we analyze the thrust mathematically?
Of course! Compare the mass flow rate of the exhaust to the desired deceleration and calculate the force needed. It's a straightforward, yet impactful application of our principles.
To summarize, understanding momentum and thrust calculations allows us to analyze launch and landing scenarios effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the mass conservation equation is applied to analyze flow conditions and calculate forces acting on bodies within moving control volumes. The principles of incompressible flow, momentum transport, and practical examples, such as jet impingement and spacecraft deceleration, are discussed to illustrate these concepts.
Detailed
Detailed Summary
In this section, we apply the mass conservation equation to analyze forces acting in moving control volumes. We start by establishing that for any incompressible flow, the outflow equals the inflow, thus emphasizing the conservation of mass. The use of Reynolds' transport theorem is pivotal for understanding momentum changes within a control volume.
Key Points:
- Mass Conservation: Inflow = Outflow, especially for incompressible flows.
- Momentum Flux: The momentum flux must be analyzed to understand the forces acting on bodies. The flow's characteristics (steady, unsteady, incompressible, etc.) significantly impact calculations.
- Applications: Several practical examples illustrate these concepts, including:
- Water Jet Impingement: Analyzing forces when a water jet strikes a flat plate.
- Spacecraft Deceleration: Understanding forces at play when a spacecraft slows down after launch.
The implications of these calculations are vast, encompassing areas of fluid dynamics, aerospace engineering, and mechanical systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Conservation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
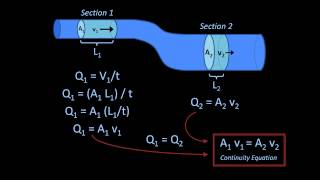
Now let us apply the mass conservation equation where is inflow minus outflow and this case will be,
Outflow = Inflow.
Incompressible flow: ρ1A1u1 = ρ2A2u2.
Detailed Explanation
The mass conservation equation states that the mass flow into a control volume must equal the mass flow out. In incompressible flow, this translates to the equation ρ1A1u1 = ρ2A2u2, where ρ is the fluid density, A is the cross-sectional area, and u is the flow velocity. This means that if you have a certain volume of fluid entering a section, the same volume must exit, provided the density remains constant.
Examples & Analogies
Imagine water flowing through a garden hose. If the hose has a wider section, water flows more slowly there than in a narrower section. This principle helps to understand why the same amount of water must flow out of the narrower section as flows in from the wider section.
Calculating Force from Momentum
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we have to find out what is the force acting in R and the R directions, we have the pressure component here. Applying Reynolds transport theorems and simplifying the tops. Here, this is the main concept that there is a change of the momentum flux within the control volume.
Detailed Explanation
In fluid mechanics, when analyzing forces acting on a control volume, we can use the Reynolds Transport Theorem (RTT) to derive relationships for momentum flux changes. The force acting on a control volume can be computed from the change in momentum flux, which considers both the inflow and outflow velocities and the pressure forces acting due to fluid dynamics.
Examples & Analogies
Consider a basketball getting shot into a hoop. The force applied to the ball changes its momentum as it travels through the air. Similarly, in fluid dynamics, the change in momentum flux helps us calculate the forces acting on objects in the flow.
Finding Force in Moving Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let’s look at a water jet impinging normal to a flat plate moving to the right at velocity Vc. Find the force required to keep the plate moving at constant velocity where the jet density is given, and the velocities of jet and frame are respectively given.
Detailed Explanation
In this example, we analyze a water jet impacting a flat plate that is moving to the right. To keep the plate moving at constant velocity, the force exerted by the water jet (which is a result of the change in momentum) must balance the forces acting on the plate. By calculating the force from momentum considerations, we can derive the necessary magnitude to keep the plate in constant motion.
Examples & Analogies
Think of a person trying to hold a sheet of paper against a steady wind. The wind exerts a force on the paper, pushing it back. To keep the paper steady, the person has to exert an equal force in the opposite direction. This balance of forces is similar to keeping the plate stable against the water jet force.
Example Problem: Horizontal Jet on Vane
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A horizontal jet of water strikes a vane turned at angle θ. The inlet area and velocity are given. We need to determine the anchoring force required to hold this vane stationary.
Detailed Explanation
In this problem, we look at a horizontal water jet striking a vane at an angle. The force required to keep the vane stationary can be determined by applying the principles of conservation of momentum and analyzing the forces acting from the incoming and outgoing water flow.
Examples & Analogies
You can visualize this by imagining a sailboat in a constant wind. The wind exerts a force on the sails, and to keep the boat from moving off course, there needs to be a countering force applied. Similarly, the vane experiences forces from the incoming and deflected water jet, requiring a balancing force to maintain its position.
Decelerating a Spacecraft Before Landing
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When a spacecraft approaches landing, it requires deceleration, which can be achieved using thrust from fuel combustion. The mass flow rate and relative velocity of exhaust play a crucial role in determining the deceleration.
Detailed Explanation
In space travel, decelerating a spacecraft before landing is a complex process. It involves calculating the thrust required based on fuel consumption (mass flow rate) and the velocity of the exhaust gases. The principles of linear momentum indicate that the thrust applied must balance the momentum change needed to slow down the spacecraft.
Examples & Analogies
Think of a car preparing to stop at a traffic light. The driver applies the brakes, which generates a force that reduces the car's momentum. In the same way, a spacecraft uses controlled thrust from rockets to produce the necessary deceleration before landing.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Conservation: The principle that mass in must equal mass out.
-
Momentum Flux: The rate of momentum transfer across a given area.
-
Reynolds Transport Theorem: A method to relate momentum changes in a control volume to fluid flow across its boundaries.
-
Control Volume: An essential tool in fluid dynamics to analyze flow behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating forces from a water jet striking a flat plate.
-
Determining the thrust needed to decelerate a spacecraft during landing.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
'In must equal out, that's what it's all about!'
📖 Fascinating Stories
-
Imagine a water fountain—water flows in and out, and the same amount always returns to keep the fountain full.
🧠 Other Memory Gems
-
To remember 'mass conservation,' think 'Keep It Equal: In and Out Fluid.'
🎯 Super Acronyms
MEME
- Mass Equals Mass Exiting (for mass conservation).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Conservation
Definition:
The principle stating that mass entering a control volume must equal mass leaving it.
-
Term: Incompressible Flow
Definition:
Flow where density remains constant throughout.
-
Term: Momentum Flux
Definition:
The amount of momentum passing through a given area per unit time.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem used to relate the change in momentum within a control volume to the flow of momentum across its boundaries.
-
Term: Control Volume
Definition:
A defined region in space through which fluid flows, used for analyzing fluid dynamics.