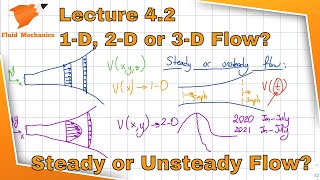
Two-Dimensional Flow Classification
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Mass Conservation in Two-Dimensional Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re going to discuss the mass conservation principle in two-dimensional flow. This principle states that mass inflow should equal mass outflow. Why do you think that is important?

Is it because it keeps the system balanced?

Exactly! This helps us maintain a steady mass flow in our analysis. When considering incompressible flow, we can simplify this further. Can anyone recall what incompressible flow means?

It means the density remains constant?

That’s correct! When dealing with incompressible flows, we can state that the density doesn’t change, making our calculations much easier.
Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s discuss the Reynolds Transport Theorem. This theorem allows us to relate the rate of change of momentum in a system to the outflux of momentum. Can someone tell me what we mean by momentum flux?

Is it the quantity of momentum being transferred through a section?

Absolutely! It’s crucial in analyzing how momentum behaves at a control volume. Why is it essential to consider relative velocities in this situation?

Because it can change the momentum experienced by the control volume?

Precisely! Considering relative velocities helps us assess the actual momentum flux effectively. Let's look at an example involving water jets.
Momentum Flux Calculation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s apply our understanding of momentum flux through an example. Imagine a water jet striking a flat plate. How do we approach calculating the force exerted on that plate?

We would need to determine the momentum of the jet and how it’s distributed when it hits the plate.

Correct! We also have to consider both influx and outflux momentum in our equations. Could anyone share what equations we would be using?

Isn’t it based on the mass flow rate and the change in velocities of the fluid?

Right! We utilize those parameters to arrive at the force, keeping in mind everything must compute to a steady state.
Real-world Applications of Momentum Concepts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's explore some real-world scenarios where these principles apply. What’d be an example of a moving control volume scenario?

A plane that changes speed by the thrust of its engines?

Yes, exactly! And how we can relate that to two-dimensional flow analysis. These concepts are not just theoretical—they have engineering and design implications.

So understanding flow helps us design better aircraft?

Absolutely, design decisions are heavily reliant on being able to predict fluid behavior using these classifications and principles.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore two-dimensional flow classification regarding mass conservation, particularly in the context of incompressible flow. It discusses the Reynolds transport theorem, flow parameters affecting momentum flux, and practical applications like water jet dynamics and their interaction with surfaces.
Detailed
Detailed Summary
This section delves into the classification of two-dimensional flow, which is essential in fluid dynamics for analyzing various flow situations. The key principles discussed include:
Mass Conservation
The fundamental principle states that the mass inflow equals the mass outflow under steady flow conditions:
$$ ext{Outflow} = ext{Inflow} $$
In the context of incompressible flows, the density remains constant, simplifying the equations applied in fluid mechanics. This leads to relationships used to determine velocity and discharge in different scenarios.
Reynolds Transport Theorem (RTT)
Using RTT, we analyze momentum exchanges within a control volume, particularly focusing on effects like momentum flux changes throughout the studied control volume. Significant assumptions are made, such as neglecting unsteady flow conditions for simplification.
Momentum Flux Components
Discussions include calculating the forces acting on two-dimensional flows, examining vector components in different directions (e.g., x and y components) and the resulting pressure impacts on fixed or moving surfaces, such as plates or jets contacting walls. The section uses specific examples, such as water jets impacting flat plates, to elucidate how to apply continuum mechanics to practical problem-solving.
Practical Applications
The examples illustrate how these principles can be utilized to derive forces on moving surfaces and the practical considerations necessary in real-world applications, emphasizing the importance of steady, turbulent, and incompressible classifications in fluid dynamics.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Flow Types
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Flow classification: Two dimensional, Steady flow, Turbulent, Incompressible.
Detailed Explanation
In fluid mechanics, flows can be classified in various ways. Here we focus on four key classifications: Two-dimensional flow refers to flow that has movement in only two directions (typically the x and y axis). Steady flow means that the fluid properties at any point in the system do not change over time. Turbulent flow is characterized by chaotic changes in pressure and flow velocity, as opposed to the smooth, orderly flow known as laminar flow. Lastly, incompressible flow indicates that the fluid density remains constant throughout the flow.
Examples & Analogies
Imagine a river (steady, two-dimensional flow) where the current flows smoothly in a consistent manner. However, during a storm, the river's flow might become turbulent, creating waves and chaotic movements. Meanwhile, the water itself remains essentially the same density (incompressible), regardless of the speed at which it flows.
Application of Conservation Equations
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now we have to apply the mass conservation equations. The mass influx is equal to mass outflux.
Detailed Explanation
The principle of mass conservation tells us that the mass entering a control volume must equal the mass leaving it, provided that there is no accumulation of mass within that volume. In a two-dimensional flow situation, we apply this to both the inflow and outflow of the fluid. Mathematically, it can be expressed as:
Influx = Outflux. This means that if we measure the mass flow rates of fluid coming into and out of an area, they must balance out over time.
Examples & Analogies
Consider a bathtub draining. When the water is flowing out of the drain at a steady rate, if you pour water in at the same rate, the water level remains constant. This balance illustrates the concept of mass conservation in a closed system.
Forces in Flow Applications
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now we have to find out what is the force acting in R and the R directions, considering the pressure component.
Detailed Explanation
In fluid dynamics, forces acting on a fluid can be analyzed through pressure differentials. When we are dealing with flows, we often need to calculate the forces on surfaces due to the pressure caused by fluid movement. For instance, if a fluid is hitting a surface, the change in momentum of the fluid as it transfers to the surface generates a force. This is derived from the momentum equations, considering both the inlet and outlet pressures.
Examples & Analogies
Think about a garden hose spraying water against a wall. The water hits the wall and pushes against it. The speed of the water and the area it covers determine how much force is exerted on the wall. This same principle applies when calculating forces in fluid flows.
Control Volume in Problems
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Movable control volume concept: Only the things we have here to know that we will apply this movable control volumes to know the pressure distribution part.
Detailed Explanation
Using a control volume approach allows us to simplify the analysis of fluid flow. A control volume is a fixed region used to analyze mass, momentum, and energy flow into and out of it. In the context of two-dimensional flow classifications, understanding how these volumes interact with the pressures involved enhances our ability to predict flow behavior. This is particularly important in systems where the volume is not static, like a moving plate with a water jet impacting it.
Examples & Analogies
Imagine a boat moving through the water. The water around the boat forms a control volume; as the boat moves forward, it pushes water aside while also affecting the pressure distribution around it. By analyzing specific volumes in this way, we can better understand the forces acting on the boat, similar to how we analyze a control volume in fluid mechanics.
Practical Examples of Fluid Flow
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us take another examples which are again simple examples what we are talking about, but is the control volume which is the moving conditions.
Detailed Explanation
In practical applications of two-dimensional flow classification, we can look at examples such as a water jet striking a plate or a fluid flowing through pipes. Each situation can be analyzed by setting up a control volume around the area of interest, applying the conservation equations, and computing forces and pressures accordingly. This systematic approach allows for accurate predictions of how fluids will behave in different configurations.
Examples & Analogies
Think of a water fountain. The water jets shooting upward and then falling back down can be analyzed as a series of control volumes. By measuring the inflow of water and the forces acting on each segment of the fountain, we can understand how to optimize its design to achieve the desired height and flow of the water.
Key Concepts
-
Mass Conservation: The mass inflow must equal the mass outflow for steady state.
-
Incompressible Flow: The density of the fluid remains constant.
-
Reynolds Transport Theorem: Used to relate changes in momentum to flux across control volume.
-
Momentum Flux: Important for calculating dynamic forces in systems.
Examples & Applications
Water jet striking a solid surface converting kinetic energy to exert force.
Analysis of aircraft dynamics considering mass conservation for thrust calculations.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Mass in must flow out, flows in and out, that's what it's about!
Stories
Imagine a river flowing steadily. No water enters or exits without flowing out—all flow equals outflow, like a balance in nature.
Memory Tools
RTT = Rate of change of Momentum = Total flux out - Total flux in.
Acronyms
MIR - Mass In equals Rejected (out).
Flash Cards
Glossary
- Mass Conservation
The principle stating that mass inflow is equal to mass outflow in a steady flow system.
- Incompressible Flow
Flow where the fluid density remains constant throughout the process.
- Reynolds Transport Theorem (RTT)
A theorem establishing a relationship between the time rate of change of momentum within a control volume and the momentum flux across its boundaries.
- Momentum Flux
The rate of transfer of momentum through a specified area.
- Control Volume
A specified region in space used to analyze fluid movement and forces acting on it.
Reference links
Supplementary resources to enhance your learning experience.
