Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Volumetric Discharge
Unlock Audio Lesson
Let's begin by discussing volumetric discharge. Can anyone tell me what constitutes volumetric discharge?
Is it the amount of fluid that passes through a given surface per unit time?
Exactly! It can be expressed as Q = A * v, where Q is the volumetric discharge, A is the area, and v is the velocity. Remember the mass conservation principle - inflow equals outflow.
So if the inflow is higher than the outflow, what happens?
Good question! If inflow exceeds outflow, it leads to accumulation in the control volume. This relates to our next topic on analyzing flow within control volumes.
Can we summarize that as 'In equals Out!'?
Yes! Great mnemonic! Let's keep that in mind as we discuss more complex applications.
Applying Momentum Flux
Unlock Audio Lesson
Now, let's analyze the momentum flux. Can anyone recall how we express momentum in fluid systems?
I think momentum is mass times velocity?
Correct! And when considering a control volume, we apply the Reynolds Transport Theorem to relate the mass flow rates of inflow and outflow to net forces acting on the system.
What does that mean practically? Could you give an example?
Sure! For instance, if a water jet strikes a plate, the momentum change creates a force we can calculate based on the jet's velocity and area. Anyone remember how we calculate the force?
Is it the product of mass flow rate and the change in velocity?
Yes! That's right! Remember, applying this appropriately takes us step-by-step through fluid mechanics fundamental.
Incompressible Flow Dynamics
Unlock Audio Lesson
Today we'll explore incompressible flow. Why is it essential for our calculations in fluid dynamics?
Because we assume density is constant, which simplifies our calculations?
Exactly! In incompressible flows, the density doesn't change and this allows us to apply the principle of continuity, further supporting mass conservation.
Can you give an example of incompressible flow?
Definitely! Think of a water jet coming out at a constant rate. Let's analyze it with the mass conservation equation. What do we expect from the inflow and outflow conditions?
When they're equal, we're at a steady state!
Exactly! Steady-state conditions show that we have a proper flow rate balance, vital for designing systems like hydraulic pumps.
Applications in Real-World Scenarios
Unlock Audio Lesson
Let's shift gears to applications. How do we apply these principles in spacecraft thrust?
By using the jet to create thrust for deceleration, right?
Exactly! The momentum flux from expelling gas upward generates thrust. What should we consider when calculating the force exerted?
We need to account for the mass flow rate and the velocity of the exhaust gases!
Correct! Let's take a specific numerical example to understand how to apply these calculations in real-time!
Can you provide a scenario?
Certainly! We could model a spacecraft using a solid fuel rocket to decrease its descent speed before landing.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section covers volumetric discharge, emphasizing the mass conservation equation and its application in analyzing fluid flow dynamics. It introduces the concepts of inflow and outflow in steady and unsteady flows and demonstrates how to calculate velocities and forces acting within control volumes in specific scenarios, including water jets and spacecraft deceleration.
Detailed
Detailed Summary of Volumetric Discharge
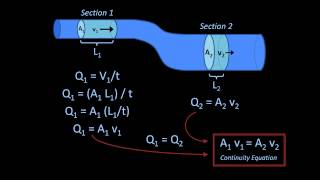
Volumetric discharge refers to the flow rate of fluid per unit area, which can be derived from the mass conservation principle. The relationship between inflow and outflow is utilized to understand various fluid dynamics scenarios, especially in steady and unsteady flows. The section discusses how incompressible fluid flow retains constant density, relating mass flux to volumetric flow rate through the area.
When analyzing fluid in control volumes, especially in applications such as water jets and spacecraft maneuvers, two key equations arise:
- Mass Conservation Equation: The inflow must equal the outflow under steady conditions, which can be represented as:
- Outflow = Inflow
- Momentum Flux: In unsteady flow situations, the change in momentum is connected with the forces acting on a system. The Reynolds Transport Theorem gives a framework to analyze momentum in a moving control volume.
The section illustrates the application of these concepts through a series of examples, including the forces acting on a flat plate due to water jet impingement and the components of momentum applied to a spacecraft using jet thrust for deceleration. Through these examples, essential parameters like velocity, mass flux, and net forces are effectively explored.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Conservation Principle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us apply the mass conservation equation: Outflow = Inflow
Detailed Explanation
The mass conservation principle states that the mass flowing into a system must equal the mass flowing out of the system when considering a closed control volume. This means that for every unit of mass entering, there must be an equal unit of mass exiting. This fundamental concept is crucial in fluid dynamics as it lays the groundwork for understanding how fluids behave in various systems.
Examples & Analogies
Imagine a bathtub with a drain. If you turn on the water and it flows in at a certain rate, for the water level to remain constant, the drain must allow water to flow out at the same rate. If more water flows in than out, the tub overflows, demonstrating the conservation of mass principle.
Calculating Velocity from Volumetric Discharge
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is what the discharge is given to us; the volumetric discharge is given to us divide by the area will get it the velocity.
Detailed Explanation
To calculate the velocity of a fluid flow, you can use the formula: velocity = volumetric discharge / area. This formula shows that if you know how much fluid is passing through a specific area over time (volumetric discharge) and you know the size of that area, you can determine the speed at which the fluid is moving. It's essential in applications ranging from plumbing to aerodynamics.
Examples & Analogies
Think of a garden hose. If you have a hose with a specific diameter and you turn on the water, the amount of water flowing out per second (volumetric discharge) divided by the cross-sectional area of the hose will give you the speed of the water flowing out.
Force Acting on Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we have to find out what is the force acting in R and the R directions, we have the pressure component here.
Detailed Explanation
When analyzing fluids in motion, it's important to consider the forces acting upon them, particularly pressure forces in different directions (R and x directions). These forces affect the movement of fluid elements within a control volume. The analysis often involves applying the Reynolds transport theorem, which connects the flow of fluids with the forces acting on them and the resulting changes in momentum.
Examples & Analogies
Imagine blowing up a balloon. As you blow air into the balloon, pressure builds inside, creating a force against the inner walls. This pressure is similar to the forces acting in fluid dynamics, where pressure changes result in movement and changes in flow direction.
Momentum Flux and Steady Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Neglecting even though flow is technically unsteady, we can assume that the flow is steady for the sake of simplifying the analysis.
Detailed Explanation
In fluid dynamics, flow can be classified as steady or unsteady. For analysis, sometimes we simplify our equations by assuming steady flow, which means that properties like velocity at a point do not change over time. This greatly simplifies calculations, particularly when analyzing momentum flux, which looks at the quantity of motion (mass times velocity) in moving fluids.
Examples & Analogies
Consider a river flowing steadily. At any point along the river, if you measure the speed and volume of water, they remain consistent over time. This is akin to assuming steady flow conditions in certain fluid dynamics calculations.
Applications to Practical Scenarios
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now take another example which is a water jet impinging this normal to a flat plate.
Detailed Explanation
In practical applications, like when a water jet strikes a flat surface, the forces and resulting momentum changes can be calculated using the principles discussed. This particular scenario demonstrates how understanding volumetric discharge and the forces in play can help design systems that utilize jets of fluid effectively, such as in hydraulic machinery.
Examples & Analogies
Think of a power washing machine. Water is ejected at high volumes and speeds, striking surfaces to clean them. Engineers must calculate the necessary force to ensure it is effective without damaging the surfaces, similar to assessing the impacts discussed in fluid dynamics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Volumetric Discharge: The flow rate of fluid through a surface area, calculated using A * v.
-
Mass Conservation: Inflow must equal outflow in steady-state conditions.
-
Momentum Flux: The rate of momentum transfer through a unit area; key to calculating forces.
-
Incompressible Flow: Fluid density remains constant, simplifying calculations.
-
Reynolds Transport Theorem: Connects momentum changes in control volumes to net flux of momentum.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating the force exerted by a water jet impinging on a plate using the principles of volumetric discharge and momentum conservation.
-
Analyzing the thrust from a spacecraft expelling exhaust gases, incorporating mass flow rates and velocities.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Inflow equals outflow, that's the flow, keep it steady for success to show!
📖 Fascinating Stories
-
Imagine a water tank filling; the inflow matches the outflow perfectly to keep the level steady—the concept reflects volumetric discharge principles.
🧠 Other Memory Gems
-
V=Q/A; visualize a stream with dummies flowing out to remember volumetric discharge.
🎯 Super Acronyms
MEMORY
- Momentum
- Energy
- Mass
- Outflow
- Rate
- Yield - key concepts in fluid dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Volumetric Discharge
Definition:
The amount of fluid flowing through a cross-sectional area per unit time.
-
Term: Mass Conservation Equation
Definition:
A principle stating that the mass inflow equals mass outflow in a steady state.
-
Term: Momentum Flux
Definition:
The flow of momentum per unit area, relevant in determining force exerted by fluids.
-
Term: Incompressible Flow
Definition:
Fluid flow where the density remains constant throughout the motion.
-
Term: Reynolds Transport Theorem
Definition:
A mathematical statement that relates the change in momentum within a control volume to the net flux of momentum across its boundaries.