Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Inflow and Outflow
Unlock Audio Lesson
Today, we're examining mass conservation in fluid dynamics. Who can tell me what inflows and outflows refer to in our context?
I think inflow is the amount of fluid entering a control volume, while outflow is the amount leaving it.
Great! Yes, when we say inflow equals outflow, we're applying the mass conservation principle. Can anyone explain why this principle is essential in fluid mechanics?
Because it helps us understand how fluids behave in systems, allowing us to make predictions about flow velocities and related pressures!
Exactly! Remember the acronym 'INPUT'—Inflow, Net flow conservation, Outflow, Utility in predictions. Let's summarize our key points.
1. Inflow and Outflow are crucial for mass balance. 2. They are the backbone of the mass conservation equation.
Momentum Flux Calculation
Unlock Audio Lesson
Now that we understand inflow and outflow, let's look at momentum flux. What is momentum flux, and why is it important?
Momentum flux is the rate of flow of momentum through a surface, right? It's important because it affects forces in fluid systems.
Excellent! Using Reynolds Transport Theorem, or RTT, we can calculate the net change in momentum flux. What does this tell us about forces in our systems?
It helps determine how forces acting on a control volume can change based on the inflow and outflow of momentum.
Correct! To remember this, think of 'FLEET': Forces from momentum, Law of conservation, Energy interaction, Equation of motion, Transfer of momentum. Let’s summarize today's concepts.
1. Momentum flux relates to forces in fluid flow. 2. RTT helps quantify changes in momentum flux.
Practical Example: Water Jet Impinging on a Plate
Unlock Audio Lesson
Let's apply our knowledge with a practical example involving a water jet striking a flat plate. What parameters will we need to analyze?
We should consider the jet's velocity, the density of the fluid, and the area of the plate.
Exactly! And we need to calculate the force exerted on the plate due to the inflowing water jet. What equations might help us here?
We could use the mass conservation equation and then apply RTT for momentum flux!
Fantastic! Remember, we can neglect some forces if the inflow is steady and the system is equilibrated. Let’s summarize our key points from today.
1. Analyze parameters like velocity and density. 2. Use equations for mass conservation and momentum flux.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concept of momentum flux changes is introduced, emphasizing the significance of mass conservation equations. It explores both incompressible flow scenarios and practical applications such as the interaction between water jets and moving plates. Key examples illustrate the calculation of forces due to momentum flux changes in various fluid dynamics situations.
Detailed
Momentum Flux Changes
In fluid dynamics, the momentum flux changes are crucial for understanding how fluids behave under varying conditions. This section primarily focuses on the following key points:
Mass Conservation Equation
The mass conservation equation can be represented as inflow minus outflow. For incompressible flow, the equation simplifies, leading to equal inflow and outflow rates. The concept is vital for analyzing systems where mass transfer is involved, considering the implications for velocity and pressure.
Calculating Forces in Fluid Systems
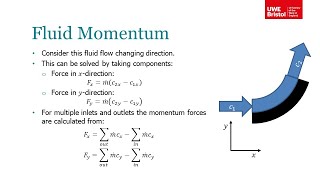
The changes in momentum flux within a control volume are not always significant compared to external forces. When the momentum thrust from sources like fuel combustion is considered, the intricate balance between inflow and outflow components is addressed using Reynolds Transport Theorem (RTT). This theorem facilitates the calculation of forces in various directions by taking into account pressure forces on surfaces in a moving control volume.
Practical Examples
Numerous practical examples illustrate the application of these principles, such as the situation where a water jet impinges on a plate. The analytical process involves establishing conditions like steady flow, turbulent characteristics, and flow classification based on dimensions.
Overall, understanding momentum flux changes and their implications allows for better predictions of fluid behavior in engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Application of Mass Conservation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us apply the mass conservation equation where inflow minus outflow. In this case, Outflow = Inflow for incompressible flow.
Detailed Explanation
The mass conservation equation states that the mass entering a control volume must equal the mass leaving the control volume when there's a steady flow, particularly in incompressible fluids. Therefore, inflow must equal outflow, maintaining consistent mass within the control volume.
Examples & Analogies
Think of a bathtub filling up with water at a constant rate. If the water is flowing in at the same rate that it flows out (say through a drain), the level of water remains stable. This is identical to how mass conservation works in fluid dynamics.
Calculating Forces on a Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we have to find out what is the force acting in R and the R directions, we have the pressure component here. Applying Reynolds transport theorem and simplifying the tops.
Detailed Explanation
In analyzing forces within a control volume, we assess both pressure components and momentum flux changes. The Reynolds transport theorem helps in connecting the movement of fluid particles and the resultant momentum changes in the control volume due to varying flows.
Examples & Analogies
Imagine pushing a swing. The force you apply determines how far the swing moves, reflecting how pressure changes in a fluid determine the forces in that fluid system.
Moment Flux Contribution in Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The change in momentum flux within a control volume is not significant compared with the momentum thrust coming from the fuel.
Detailed Explanation
When observing the changes in momentum flux, the primary factors often include external thrusts, such as those generated from fuel combustion, rather than internal changes within the fluid's movement. These thrusts significantly impact the overall momentum in the system.
Examples & Analogies
Consider a rocket launch. The thrust generated by the rocket’s engines creates a far greater effect on its upward movement than any minimal changes in airflow around the rocket as it ascends.
Momentum Flux in x-Direction and Resultant Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
By applying relevant equations, the momentum flux in the x-direction contributes to the force calculated, resulting in the force acting on the x direction.
Detailed Explanation
In fluid dynamics, the momentum flux in any direction can be found by multiplying the density, velocity, and the cross-sectional area through which the fluid is flowing. The resultant force in the x-direction from this momentum flux allows engineers to predict how much force acts on objects within a fluid.
Examples & Analogies
Think of a fire hose. The pressure from the water forcing through the nozzle generates a specific force in the direction that the hose is aimed. The faster the water and the wider the nozzle, the more force can be exerted.
Example: Water Jet Impinging on a Moving Plate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A water jet impinges normal to a flat plate that moves to the right. Find the force required to keep the plate moving at constant velocity.
Detailed Explanation
In this example, the water jet's behavior as it strikes the moving plate and splits into upward and downward directions must be analyzed. The momentum conservation laws apply and help determine the forces acting on the system through fluid interaction.
Examples & Analogies
Imagine standing in front of a sprinkler. As water sprays out and hits you, it pushes you back. The force you need to exert just to remain still is similar to the forces analyzed in this example.
Mass Influx and Outflux Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mass influx is equal to mass outflux as we consider relative velocity components within this context.
Detailed Explanation
The mass entering and exiting the control volume needs to be balanced to maintain the steady-state flow, where the relative velocities help in determining the changes in mass flow rates across the surfaces.
Examples & Analogies
Think of a revolving door at a busy entrance. The number of people entering (influx) must equal the number of people leaving (outflux) to keep the door moving smoothly and prevent blockage.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Momentum Flux: The rate at which momentum is transferred in a fluid system.
-
Mass Conservation: The principle that mass is neither created nor destroyed in a closed system.
-
Reynolds Transport Theorem: A tool used to relate momentum changes in a control volume with flows across its boundaries.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating the momentum flux of a jet of fluid striking a flat plate.
-
Using Reynolds Transport Theorem to evaluate forces acting on moving plates in a jet flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Inflow, outflow, it’s all a show; Momentum shifts, this you should know.
📖 Fascinating Stories
-
Imagine a river flowing into a pond. The water enters (inflow) and leaves (outflow) through a stream. Understanding this gives you the essence of mass conservation!
🧠 Other Memory Gems
-
Remember 'FLEET' for Forces, Law, Energy, Equation of motion, Transfer; it encapsulates momentum dynamics.
🎯 Super Acronyms
INPUT stands for Inflow Net, Outflow Utility
- a: reminder of mass conservation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Momentum Flux
Definition:
The rate of transfer of momentum through a unit area in a flow field.
-
Term: Reynolds Transport Theorem (RTT)
Definition:
A mathematical formulation that relates the change in momentum of fluid within a control volume to the net flow of momentum across its boundaries.
-
Term: Incompressible Flow
Definition:
A flow regime where the fluid density remains constant irrespective of the changes in flow conditions.
-
Term: Control Volume
Definition:
A specified region in space through which fluid flows, used to analyze fluid dynamics.
-
Term: Mass Conservation Equation
Definition:
An equation that expresses the principle that mass is conserved in a fluid system.