Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Mass Conservation in Control Volumes
Unlock Audio Lesson
Today, we’ll explore the mass conservation equation. Can anyone tell me what we mean by inflow and outflow in a control volume?
Isn't inflow the mass entering the control volume while outflow is the mass leaving it?
Exactly! The basic principle is that for a closed control volume, the inflow must equal the outflow. You can remember this with the acronym 'I=O'.
What if the flow is incompressible, like liquids?
Good point! For incompressible flow, the densities remain constant, which simplifies our calculations significantly. Let’s keep building on this understanding.
Can you give an example of inflow and outflow?
Certainly! Consider a pipe with water flowing. The amount of water entering must equal the amount leaving if the pipe is at steady state. So, mass conservation holds true.
In summary, mass conservation is crucial for analyzing control volumes in fluid dynamics.
Momentum Equations and Reynolds Transport Theorem
Unlock Audio Lesson
Next, let’s discuss the momentum equations. Who remembers how the momentum changes within a control volume?
Is it based on the forces from inflow and outflow?
Correct! The momentum flux change accounts for forces acting on the control volume. Remember the saying, 'More momentum in, more momentum out'.
How does this relate to the Reynolds transport theorem?
Great question! The Reynolds transport theorem allows us to relate the rate of change of momentum in a control volume to net outflow, incorporating both mass flow rates and velocities. This forms the backbone of many fluid dynamics problems.
Can we see this in action with an example?
Absolutely! In the following session, we will work through an example involving a water jet impacting a plate.
Applications with Moving Control Volumes
Unlock Audio Lesson
Let’s dive into moving control volumes. How does movement influence our calculations?
Does the velocity of the control volume affect inflow and outflow?
Exactly! If our control volume is moving, we need to account for relative velocities. Imagine a water jet striking a flat plate that is also moving.
What parameters should we consider in our calculations then?
We’ll need to consider the velocities of the jet, the plate, and how these interact to affect momentum. Always remember 'velocity matters' when calculating forces!
Can you summarize the key concepts from this session?
Certainly! When analyzing moving control volumes, incorporate relative velocities of inflows and outflows. This influences outcomes significantly.
Practical Examples and Problem Solving
Unlock Audio Lesson
Let's apply what we learned through a practical example. Imagine a water jet with a specified density hitting a plate. How do we calculate the force?
Do we use momentum equations here?
Exactly! We calculate the momentum imparted on the plate by the jet flow, and from that, determine the net force required. How does the equation look?
It might be something like force = mass flow rate × change in velocity?
Spot on! You’ll compute force as the momentum change per time. Remember this formulation as it shows how momentum results in forces.
Can we predict forces in another example too?
Absolutely! We can evaluate different scenarios, altering parameters to observe how forces change. This understanding is vital in engineering applications.
Flow Classifications and Their Importance
Unlock Audio Lesson
Lastly, let’s review flow classifications we mentioned earlier. How do these classifications influence our analyses?
Do they determine which equations we can use or how to simplify our models?
Exactly! Understanding whether a flow is laminar vs turbulent or incompressible vs compressible is crucial for selecting applicable equations and methods.
How can we differentiate between laminar and turbulent flows?
Laminar flow is characterized by smooth, orderly motion, while turbulent flow has chaotic changes. An easy mnemonic is 'Turbulent Timmy runs wild!'
What’s next in our learning?
Next, we’ll solve exercises to reinforce our understanding of these concepts! Remember, 'Practice makes perfect'!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the principles of mass conservation (inflow versus outflow), the implications of momentum flux change within a control volume, and presents examples illustrating these concepts. The importance of steady flow assumptions and the classifications of flow types are also highlighted.
Detailed
This section discusses the application of the mass conservation equation (inflow vs outflow) for control volumes in fluid mechanics. It introduces the momentum equations resulting from the change in momentum flux within control volumes. By deriving these equations, the significance of Reynolds transport theorem is emphasized, along with the implications of simplifying assumptions such as steady flow and incompressibility. The section includes practical examples, such as calculating forces on flat plates influenced by water jets and explaining fluid interaction with moving control volumes. Key flow classifications, including two-dimensional, steady, turbulent, and incompressible conditions, are also presented, contributing to a solid understanding of how momentum equations are applied across various scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Conservation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us apply the mass conservation equation where inflow minus outflow and this case will be, Outflow = Inflow. Incompressible flow: ρ1 A1 V1 = ρ2 A2 V2
Detailed Explanation
The mass conservation equation expresses that for a fluid flowing through a control volume, the mass inflow must equal the mass outflow. In this case, if the flow is incompressible, the density (ρ) remains constant, which simplifies the equation to ρA1V1 = ρA2V2, indicating that for any cross-section, the product of area and velocity must remain equal across the control volume.
Examples & Analogies
Imagine a garden hose. If you cover part of the hose with your thumb, the water must move faster at that point to ensure that the volume of water flowing through remains constant—this is akin to the mass conservation principle in fluid dynamics.
Forces Acting on Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we have to find out what is the force acting in R and the R directions, we have x y the pressure component here. Applying this Reynolds transport theorems and the simplifying the tops.
Detailed Explanation
To determine forces acting on a control volume in the x and y directions, we need to consider both pressure and momentum flux. By applying Reynolds transport theorem, which relates the change in momentum within a control volume to the net flow of momentum across its boundaries, we can compute necessary forces. This involves analyzing pressure acting over surface areas and the changes in momentum due to incoming and outgoing streams.
Examples & Analogies
Think of a water fountain. The water jets exert forces on the fountain's base. The momentum transferred to the surroundings when water exits at a specific speed represents the dynamically balanced forces at play, similar to how we analyze forces in a fluid control volume.
Momentum Flux Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Then we have two momentum flux components, one is influx another is outflux. Beta is equal to the 1. So if I apply it, I will have a simply the momentum flux in x direction, the pressure into the area and that what I will get it and in terms of value, I will get it 355 approximately Newton.
Detailed Explanation
When we analyze fluid flow, we categorize the momentum flux into two components: influx (flow entering) and outflux (flow leaving). Here, we set beta (the efficiency or coefficient of discharge) equal to 1, suggesting that there are no losses in the flow through the area. By calculating the pressure multiplied by area for the flow entering and leaving, we can determine the net force acting on the control volume—in this case, about 355 Newtons.
Examples & Analogies
Imagine squeezing a balloon. If you apply pressure on the balloon (like an influx) on one end, the air (or fluid) inside pushes back with equal force on the other end. This force balance reflects how momentum flux and pressure relate in a control volume.
Defining Control Volumes in Flow Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
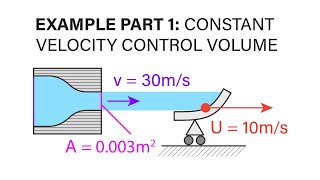
Let us take another example, a water jet impinging this normal to a flat plate and moves to the right to the velocity Vc, okay this that means, this flat forms is moving with a velocity Vc.
Detailed Explanation
In modeling fluid flow problems, defining the appropriate control volume is crucial. Here we have a water jet striking a flat plate, which is also moving horizontally. The velocities of both the jet and the plate can affect the analysis of the force required to keep the plate moving at a constant speed, highlighting the importance of relative velocities in fluid dynamics assessments.
Examples & Analogies
Consider a car moving through the rain. The speed of the car affects how the raindrops hit the windshield—just as the water jet's velocity affects the forces on the plate. Understanding how these velocities interact allows for better control and engineering design in fluid systems.
Application of Mass Continuity Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The mass influx is equal to mass outflux. If that is the conditions you have these values, okay. Please remember it we consider here the relative velocity component along.
Detailed Explanation
When analyzing the operation of moving control volumes, the mass continuity equation states that the mass entering a system must equal the mass exiting, thereby maintaining balance. This ensures consistent analyses of the velocities and densities involved as the fluid moves and splits, especially in scenarios like jets where portions of flow diverge.
Examples & Analogies
Think of a party where everyone must exit through a single door at a steady pace. If too many people try to leave at once, the flow is disrupted—much like how we must maintain mass flow rates across control volumes to ensure smooth operations in fluid dynamics.
Momentum Conservation in Jet Flow Example
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now I am applying momentum conservation equation. We remember it I need to apply the relative velocity component here...
Detailed Explanation
The momentum conservation equation states that the change in momentum of a control volume must account for the inflow and outflow of momentum across its boundaries. By substituting relative velocity components for the inflows and outflows, we can calculate the net force acting due to the jet's interaction with the surface, thereby quantifying how the system behaves dynamically.
Examples & Analogies
Consider throwing a ball. The force you exert changes the ball's momentum; similarly, the jet's interaction with surfaces modifies the momentum moving through the control volume. This analogy helps illustrate how momentum dynamics function in practical scenarios.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume: A specified region in space for fluid analysis.
-
Mass Conservation: The principle governing inflow and outflow balance.
-
Momentum Flux: Rate of momentum transfer across surfaces.
-
Incompressible Flow: Flow where density remains constant for simplifications.
-
Reynolds Transport Theorem: Relating control volume changes with flow across surfaces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating force on a plate by a water jet based on flow parameters.
-
Estimating momentum change in a moving control volume scenario with jet velocity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When mass flows in, it must flow out, to keep the equation without a doubt.
📖 Fascinating Stories
-
Imagine a busy water park where slides bring water in, but every inch leaving creates a splash! That’s like our control volumes!
🧠 Other Memory Gems
-
'REMT' - Remember Energy, Momentum, Transport for momentum equations!
🎯 Super Acronyms
'CIM' - Control, Inflow, Momentum for recalling key principles in fluid dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A specified region in space through which fluid flows to analyze mass, momentum, and energy transfer.
-
Term: Mass Conservation
Definition:
A principle stating that mass cannot be created or destroyed in a closed system.
-
Term: Momentum Flux
Definition:
The rate of momentum transfer per unit area.
-
Term: Reynolds Transport Theorem
Definition:
A mathematical theorem relating the change of momentum in a control volume to the flow of momentum across its boundaries.
-
Term: Incompressible Flow
Definition:
Flow in which the fluid density remains constant.
-
Term: Turbulent Flow
Definition:
A type of flow characterized by chaotic, irregular motions.