Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Mass Flow Rate
Unlock Audio Lesson
Today, we're going to talk about mass flow rate. Can anyone tell me what mass flow rate means?
Isn’t it about how much mass passes through a certain area in a given time?
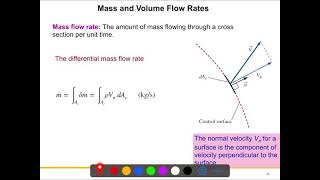
Exactly! The mass flow rate is defined as the mass per unit time. We can express it as ṁ = ρ × A × v, where ṁ is mass flow rate, ρ is density, A is cross-sectional area, and v is velocity.
What happens if we consider incompressible flow?
Good question! In incompressible flow, we simplify our equations because the density remains constant throughout. So, inflow equals outflow.
Can we just assume the same density when calculating?
Yes, when density is constant, we often assume it simplifies calculations significantly.
So, it always fits for water since it is mostly incompressible?
Absolutely! Water jet examples will illustrate this point. Remember the acronym 'I.O.' for Inflow equals Outflow—it’s key to remembering mass conservation.
Thrust Calculation
Unlock Audio Lesson
Now, shifting gears to thrust calculation, can someone define thrust?
Thrust is the force which moves an object, usually associated with jets and rockets.
Correct! It's generated by the change in momentum of the jet stream. The formula we often use is F = ṁ × (v_out - v_in).
So we're looking at the difference in velocity at the outflow versus the inflow?
Exactly! When calculating thrust, we must account for all velocity components involved.
And how does the control volume concept fit into this?
The control volume helps us analyze forces acting within a specified region. Forces can be calculated by applying the Reynolds Transport Theorem to track changes in momentum.
What about practical applications, like in rockets?
In rockets, the gas expelled at high velocity creates thrust needed to lift off, adhering to Newton's third law. So, remember 'F = mΔv' as a concise memory aid!
Practical Applications
Unlock Audio Lesson
Let's apply these concepts to real-world scenarios. Consider a water jet striking a plate. What factors do we need to calculate the force on the plate?
We need the velocity of the jet, the area of impact, and the density of the water.
Great! Now, if the water jet has a velocity of 20 m/s and plate area of 3 cm², how would we express that in terms of force?
I think we use F = ṁ × v, but we should convert the area first for mass flow rate.
Correct! Remember to convert all units consistently. If density is 1000 kg/m³, how would we calculate the mass flow rate?
So, ṁ = ρ × A × v, where we input our values!
Exactly! This method allows you to directly calculate force. Always keep in mind the flow classification for different problems!
So, would this apply similarly for spacecraft landing calculations?
Definitely! Both processes follow similar principles of thrust and momentum conservation. Think of 'A-S-T-R-O' for Area, Speed, Thrust, Rocket, and Output to remember key rocket science factors!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the principles of mass flow rate and thrust calculations are explored through the application of conservation of mass and momentum equations. The discussion covers how inflow equals outflow in incompressible flows, the effect of momentum flux changes, and practical examples involving water jets and spacecraft landing scenarios.
Detailed
In this section, we delve into the calculation of mass flow rates and thrust using fundamental principles from fluid mechanics. We begin by stating the conservation of mass, where inflow equals outflow, particularly relevant in scenarios involving incompressible flow. The section emphasizes the dynamics of thrust calculation through momentum conservation and the Reynolds transport theorem, illustrated with practical examples such as water jet applications and spacecraft deceleration upon landing. The momentum flux change generated by inflow and outflow is critically reviewed, allowing for an understanding of forces acting within a control volume in various fluid dynamics situations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Conservation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us apply the mass conservation equation where inflow minus outflow. In this case, it will be: Outflow = Inflow.
Detailed Explanation
The mass conservation equation states that the mass flow rate entering a control volume must equal the mass flow rate leaving that control volume in a steady state. This means that any mass entering the system must come out, which is a fundamental principle in fluid mechanics.
Examples & Analogies
Imagine a water tank with a faucet at the top and a drain at the bottom. If water flows in at a constant rate but does not flow out, the tank will eventually overflow. Similarly, in the context of mass flow, if more mass enters a system than exits, the system’s mass will increase, violating the conservation of mass.
Discharge and Velocity Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is what the discharge is given to us; the volumetric discharge is given to us divided by the area to get the velocity.
Detailed Explanation
The volumetric discharge, typically represented as Q (cubic meters per second), divided by the cross-sectional area A (square meters) gives us the flow velocity v (meters per second) using the formula v = Q/A. This is crucial for understanding how fast the fluid is moving through a specific cross-section.
Examples & Analogies
Consider a garden hose. If you know how much water is flowing through the hose (like the volumetric discharge) and the diameter of the hose (cross-sectional area), you can easily calculate how fast the water is coming out—just like finding the velocity of fluid flow in a pipe.
Momentum Flux and Force Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we have to find out what is the force acting in the x and y directions due to pressure components, applying Reynolds transport theorem and simplifying the terms.
Detailed Explanation
To find the forces acting on a fluid, we apply the Reynolds Transport Theorem, which connects the change in momentum within a control volume to the momentum flux at its boundaries. The force can be calculated by considering the differences in momentum flow entering and leaving the control volume.
Examples & Analogies
Think of holding a big sheet of cardboard as the wind blows against it. The wind creates a force pushing against the cardboard. By knowing the wind's speed (momentum) and how much area is being hit by the wind, you can estimate how hard you need to hold the cardboard in place.
Applying Steady Flow Assumptions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Neglecting this unsteady flow behavior, we simplify the problem by assuming steady-state conditions.
Detailed Explanation
In many fluid flow problems, assuming steady flow simplifies the calculations because the properties of the fluid at any point do not change with time. This assumption is valid when fluctuations are minimal or when examining averaged conditions over a short time period.
Examples & Analogies
Imagine riding a bike at a constant speed on a flat road. If you assume that the road ahead remains straight and flat, you can concentrate on maintaining your speed without worrying about constant changes in terrain—that's how steady state simplifies fluid dynamics.
Example of Water Jet Impinging on a Plate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A water jet of velocity V impinges normal to a flat plate that moves to the right at velocity Vc. Find the force required to keep the plate moving at constant velocity.
Detailed Explanation
This scenario involves calculating the net force required when a water jet hits a moving plate. The force can be determined using the momentum change due to the jet and the motion of the plate. The basic principle is to look at how much momentum is added to the plate and how much needs to be countered to keep it moving steadily.
Examples & Analogies
Imagine standing in a stream of water while holding a paddle. If the water hits your paddle, you will feel a force pushing it backward. If you keep pushing forward with your paddle, you’re applying a force that counteracts the water's push. Similarly, the plate must exert force to counteract the momentum from the water jet.
Momentum Change in Unsteady Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the absence of external forces, the change of momentum flux within the control volume must account for the net outflow of momentum.
Detailed Explanation
In situations where external forces don't act, the rate of momentum change within a system balances the momentum flux out of it. This principle is instrumental in analyzing systems like rockets, where expelled gas results in thrust.
Examples & Analogies
Think of a balloon filled with air. When you release the balloon, the air rushes out. The momentum of the escaping air creates a thrust that propels the balloon forward. This example shows how momentum conservation helps understand propulsion in engines.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Flow Rate: Defined as the amount of mass flowing through a cross-section per unit time.
-
Thrust Generation: Relies on the change in momentum from inflow to outflow of a fluid.
-
Incompressible Flow: Simplifies many calculations as density remains constant.
-
Reynolds Transport Theorem: Useful for analyzing momentum changes in control volumes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A water jet with a velocity of 20 m/s impacts a plate with a cross-sectional area of 3 cm², applying the concepts of thrust and mass flow rate to calculate the force exerted.
-
During spacecraft deceleration, the solid fuel rocket expels gases at a specific mass flow rate, allowing the calculation of thrust based on the relative velocity of expelled gases.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mass flow rates can change with speed, density, area take the lead.
📖 Fascinating Stories
-
Imagine a powerful water jet, like a knight with a sword, striking through air and water, creating thrust to pierce through obstacles.
🧠 Other Memory Gems
-
Think 'I.O.' for Inflow Equals Outflow to remember mass conservation.
🎯 Super Acronyms
Use 'A-S-T-R-O' for Area, Speed, Thrust, Rocket, and Output to remember rocket dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Flow Rate (ṁ)
Definition:
The measure of mass passing through a given area over a specified time, calculated as ṁ = ρ × A × v.
-
Term: Incompressible flow
Definition:
A type of flow where the fluid density remains constant, often assumed to be true for liquids like water.
-
Term: Thrust
Definition:
The force exerted by a fluid jet or rocket engine, calculated as the change in momentum per time.
-
Term: Reynolds Transport Theorem
Definition:
A theorem used in fluid mechanics to analyze the flow of mass, momentum, and energy within a control volume.
-
Term: Control Volume
Definition:
A defined region in space through which fluid flows, used to apply conservation laws.