Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Mass Conservation in Fluid Dynamics
Unlock Audio Lesson
Today, we'll start by discussing the principle of mass conservation in fluid dynamics. What do you think happens when fluid enters and exits a control volume?
I think the mass that comes in has to be equal to the mass that goes out.
Exactly! This is expressed as 'Outflow = Inflow'. This principle is fundamental in analyzing fluid systems. Can anyone think of a real-life example where mass conservation applies?
Maybe in a water pipe? The amount of water entering a pipe should equal the amount exiting it, right?
Great example! This leads us to think about how we can apply this to the momentum conservation equations. Remember, in incompressible flow, density remains constant.
So, does that mean the velocity changes if the cross-sectional area of the pipe changes?
Yes, that's correct! According to the continuity equation, velocity will inversely change with pipe area. Let’s summarize: mass entering equals mass exiting, and changes in velocity stem from pipe diameter variations.
Reynolds Transport Theorem
Unlock Audio Lesson
Now let's discuss the Reynolds Transport Theorem, also known as RTT. Can anyone explain what it does?
Isn't it about changing the control volume perspective?
Exactly! RTT helps us analyze the changes in momentum when fluid crosses a control volume boundary. This is crucial when examining fluid jets striking a surface. How do you think we can apply RTT to force calculations?
We calculate the momentum change and set up the equations to find the net force?
That's right! Remember to look for changes in incoming and outgoing momentum fluxes. Forces can be derived from these calculations effectively.
So we just tally the fluxes and solve for the force acting on the object?
Correct! This is a vital skill. Always remember: analyze the system by looking at how momentum is conserved between inflow and outflow.
Application Example: Water Jet Striking a Plate
Unlock Audio Lesson
Let’s look at an example where a water jet impinges on a flat plate. How would we set up this problem?
We would need the velocity of the jet and the area where it strikes the plate.
Exactly! From there, we can calculate the momentum change. If we have a jet velocity of 20 m/s and an area of 3cm², what's the first step?
I think we would find the mass flow rate first?
Yes! Calculate the volumetric flow rate, then convert it to mass flow rate using the density of water. What can we do once we have that?
We can apply the momentum equations to determine the force acting on the plate!
Exactly! This real-world example demonstrates the application of our theory. Remember, practical applications reinforce our understanding.
Deceleration of Spaceship
Unlock Audio Lesson
Let’s dive into a more complex scenario – a spacecraft decelerating before landing. Who can summarize how momentum conservation helps here?
The spacecraft experiences a thrust from its rocket engines that affects its momentum as it lands.
Correct! The thrust generated by the expelled gases must counter the spacecraft's downward momentum. So, if the mass flow rate of the gases is known, how does that help?
We can calculate how much the spacecraft slows down by using the conservation equations.
You're spot on! These calculations are essential in aerospace engineering. To summarize, the balance between thrust and weight must be managed for a safe landing.
So this approach applies to many engineering problems that involve changes in fluid momentum?
Absolutely! Always think of fundamental principles impacting design and operation across various systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the principles of mass conservation and momentum flux are applied to different fluid flow scenarios, including incompressible flow and moving control volumes. Key examples demonstrate how to calculate forces acting on structures exposed to fluid jets, emphasizing the significance of momentum transfer.
Detailed
Momentum Conservation Equation Application
This section focuses on applying the momentum conservation equations, particularly within fluid dynamics, where momentum and mass conservation principles are essential. The key points cover how the inflow and outflow of mass can be equated (
Outflow = Inflow) in the context of incompressible flow.
Using specific examples, the section illustrates how to determine forces acting on an object due to fluid interaction, particularly in scenarios involving moving control volumes, such as a water jet striking a flat plate or a spacecraft decelerating upon landing. The momentum conservation principles are revisited, including Reynolds Transport Theorem (RTT) and the simplification of momentum flux calculations, enabling readers to grasp how external and internal forces from the fluid contribute to total force calculations. Such applications underscore the practicalities and applications of fluid dynamics principles in real-world engineering scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Applying Mass Conservation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us apply the mass conservation equation where is inflow minus outflow and this case will be, Outflow = Inflow.
Detailed Explanation
The mass conservation equation is essential in fluid dynamics, stating that the mass entering a system must equal the mass exiting it when no mass is stored in the control volume. In this context, the outflow equals the inflow, indicating a steady-state where the amount of mass coming in is the same as the mass going out.
Examples & Analogies
Consider a bathtub with the drain open while the faucet is running. If the amount of water flowing from the faucet (inflow) equals the amount flowing out the drain (outflow), the water level stays constant. This is similar to the mass conservation equation, where mass flowing in and out remains unchanged.
Momentum Flux and Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
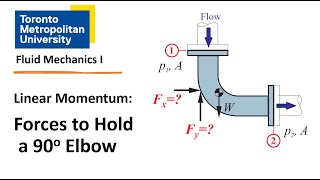
Now we have to find out what is the force acting in R and the R directions, we have the pressure component here. Applying this Reynolds transport theorems and simplifying the tops.
Detailed Explanation
To analyze the forces acting on the system, we employ the Reynolds transport theorem (RTT), a fundamental theorem in fluid dynamics that connects the rate of change of momentum within a control volume to the momentum flux crossing its boundaries. Here, we focus on the change of momentum flux due to pressure bodies in the flow, leading to resultant forces.
Examples & Analogies
Imagine you are pushing a swing. The force you exert changes the momentum of the swing. Similarly, in fluid dynamics, the pressure exerted by flowing fluids creates changes in momentum within a control volume, leading to the application of forces that affect the flow.
Calculating Force from Momentum Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For the force acting in the x direction, the momentum flux is expressed as pressure acting over area. This leads to determining the net force in the x direction.
Detailed Explanation
The momentum flux in a given direction can be determined by calculating the product of pressure and the area over which it acts. This pressure-area product contributes to the net force acting on the fluid in the x direction. When we calculate these values and sum them, we arrive at the force exerted by the fluid.
Examples & Analogies
Consider how pushing against a flat surface with a basketball creates a force due to the pressure exerted by the ball on your palm. The larger the area of contact (your palm), the greater the total force, similar to how pressure times area results in the momentum flux force.
Factors Influencing Momentum and Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we apply the mass conservation equations and momentum conservation equation to relate the velocities and the forces acting in x and vertical directions.
Detailed Explanation
By applying both mass and momentum conservation equations, we analyze how the velocities of the inflow and outflow relate to each other and to the forces in both horizontal (x) and vertical directions. Each velocity impacts the momentum flux differently, allowing us to derive necessary forces required to maintain equilibrium.
Examples & Analogies
Think of a water slide. As kids slide down, they gain speed due to gravity (momentum), while the water flowing up from the bottom adjusts to maintain a constant flow (mass conservation). The faster they slide down (higher velocity), the more forceful the push of water must be to maintain consistent flow, illustrating the relationship between velocity, mass, and momentum.
Impinging Jet and Control Volume Application
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
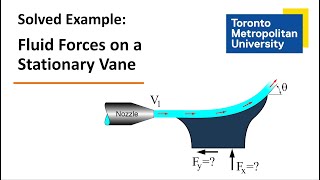
Now take another example which is a control volume where a water jet impinges on a moving plate.
Detailed Explanation
In the scenario of a water jet striking a moving plate, we can apply the concepts of the control volume to determine the forces acting on the plate. The water jet's velocity and area determine how much momentum the jet transfers to the plate, which can be calculated by integrating the momentum conservation principles.
Examples & Analogies
Imagine a skateboarder hitting a ramp riding down from a slope. The speed and volume of water from a fire hose hitting them can be compared to the water jet hitting the plate. Just like the skateboarder would feel forceful water impact, the plate experiences substantial force from the water jet, illustrating the momentum transfer concept.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Conservation: Ensures that the amount of mass in a system remains constant unless added or removed.
-
Momentum Flux: The rate at which momentum passes through a unit area.
-
Reynolds Transport Theorem: Connects the rate of change of momentum within a volume to the flux across its boundaries.
-
Control Volume Analysis: A method used to analyze fluid flow and forces acting on surfaces.
-
Force Calculation: Determined using momentum changes, specifically from inflow and outflow in fluid dynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A water jet with a velocity of 20 m/s strikes a flat plate, requiring calculations of the force exerted based on mass flow rate and area of impact.
-
A spacecraft uses thrust generated by its rocket engines to decelerate upon landing, calculated using mass flow rate of expelled gases and their velocity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Inflow and outflow, mass must stay, conserved in motion, in every way.
📖 Fascinating Stories
-
Imagine a water tank filling from a hose. The amount coming in matches perfectly with the amount leaving through a pipe, illustrating mass conservation.
🧠 Other Memory Gems
-
Momentum = Mass x Velocity (M=mv) to remember how to calculate momentum quickly.
🎯 Super Acronyms
RTT for Reynolds Transport Theorem, Remember Total Transfer!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Momentum
Definition:
A measure of the motion of an object, calculated as the product of an object's mass and velocity.
-
Term: Mass Conservation
Definition:
A principle stating that the mass of a closed system must remain constant over time.
-
Term: Reynolds Transport Theorem (RTT)
Definition:
A fundamental theorem in fluid mechanics that relates the rate of change of a quantity within a control volume to the flux of that quantity across the control surface.
-
Term: Flux
Definition:
The quantity of fluid that passes through a unit area per unit time.
-
Term: Control Volume
Definition:
An imaginary volume in space through which fluid flows, used to analyze flow and conservation principles.