Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Reynolds Number
Unlock Audio Lesson
Today, we're diving into the critical Reynolds numbers and their significance in determining fluid flow types. Can anyone tell me what the Reynolds number is?
Is it the ratio of inertial forces to viscous forces?
Exactly! The Reynolds number (Re) is defined as Re = ρuL/μ, where ρ is fluid density, u is velocity, L is the characteristic length, and μ is dynamic viscosity. Let’s keep it in mind! It helps us classify the type of flow we might have.
So, a higher Reynolds number means more turbulence, right?
Correct! Higher values signify inertial forces dominate, leading to turbulent flow.
What about the lower values?
The lower values are indicative of laminar flow where viscous forces dominate. Great questions everyone! Let's summarize: the Reynolds number helps us predict flow characteristics based on the forces at play.
Critical Reynolds Numbers
Unlock Audio Lesson
Now, let’s discuss the critical Reynolds numbers. What do you think happens at Re = 100,000?
That’s where laminar flow transitions into the transitional phase.
Correct! It’s the boundary separating laminar from turbulent flow. And what about Re = 3,000,000?
That’s where flow definitely becomes turbulent!
Exactly! Between these two critical points lies a transitional zone where flow dynamics can fluctuate. What does that suggest about design applications?
We need to design systems that can handle these transitions smoothly.
Well said! It’s crucial for engineers to account for these behaviors in various applications.
Importance of Boundary Layers and Flow Regimes
Unlock Audio Lesson
Let’s relate Reynolds numbers to boundary layers. Can somebody explain what a boundary layer is?
It’s a thin layer near the surface where viscosity has a significant effect on flow.
Right! In laminar flow, the boundary layer is stable and smooth, whereas in turbulent flow, it is chaotic and filled with eddies. How do Reynolds numbers inform us about when these transitions occur?
They give us a way to measure when laminar becomes turbulent.
Absolutely! Understanding this helps in predicting behavior and optimizing designs. Always remember, Re below 100,000 represents laminar, between 100,000 and 3,000,000 is transitional, and above 3,000,000 features turbulent flow.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section examines the formulation of the Reynolds number and the impact it has on characterizing fluid flow regimes. It details how varying Reynolds numbers influence boundary layer behavior and introduces the critical Reynolds numbers that distinguish between laminar, transitional, and turbulent flows.
Detailed
Detailed Summary
This section delves into the concept of Reynolds numbers in fluid mechanics, focusing on their role in classifying flow regimes as laminar, transitional, and turbulent. The Reynolds number is defined as the ratio of inertial forces to viscous forces and is pivotal for understanding how fluids behave under different conditions.
The critical Reynolds numbers are highlighted:
- Laminar Flow occurs when the Reynolds number is less than 100,000 (1 lakh), indicating a predominance of viscous forces and smooth flow.
- Transitional Flow exists between 100,000 and 3,000,000 (3 million), as the flow becomes increasingly complex, with flows that can fluctuate between laminar and turbulent characteristics.
- Turbulent Flow is identified when the Reynolds number exceeds 3,000,000. In this regime, inertial forces dominate, leading to chaotic and irregular motion.
Additionally, this section integrates the importance of boundary layers near solid surfaces where flow characteristics change. Understanding critical Reynolds numbers helps in designing systems to control flow characteristics effectively, which holds substantial significance across various engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Reynolds Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Reynolds numbers what we consider for a boundary layers as v is free stream velocity x is characteristic length from this is the end from this x value by the mu dynamic viscosity.
Detailed Explanation
Reynolds number is a dimensionless quantity used to predict flow patterns in different fluid flow situations. In this case, the Reynolds number is defined specifically for boundary layer flows. It is calculated using the formula: Re_x = (v * x) / μ, where 'v' is the free stream velocity, 'x' is the characteristic length (the distance along the plate), and 'μ' is the dynamic viscosity of the fluid. A high Reynolds number indicates that inertial forces are dominant compared to viscous forces, suggesting that the flow could be turbulent.
Examples & Analogies
Think about riding your bicycle on a smooth road versus riding it through a marshy area. When on a smooth road (high Reynolds number), your bicycle moves quickly with less resistance (inertia dominates). In contrast, in the marsh, the bike struggles due to mud (viscous forces dominate), which parallels how different Reynolds numbers affect flow properties.
Critical Reynolds Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the Reynolds numbers is lesser than these this is critical Reynolds numbers then flow is laminar which is easy for us okay. We can think it that to get analytical solutions for that that is what we will discuss.
Detailed Explanation
The concept of critical Reynolds numbers is essential for determining the flow regime. If the Reynolds number is less than 100,000 (1 lakh), the flow is classified as laminar. In laminar flow, the fluid moves in parallel layers with minimal mixing. This regime allows for analytical solutions, making it easier to predict flow behavior. Conversely, a Reynolds number greater than 3,000,000 (3 million) indicates a turbulent flow, where the fluid exhibits chaotic and irregular motion, complicating analytical calculations.
Examples & Analogies
Imagine a river. In the calm sections (laminar flow), the water moves smoothly without turbulence, much like syrup flowing in a straight line. In contrast, in sections where the water rushes over rocks (turbulent flow), it's all chaotic, splashing and mixing, which embodies turbulent flow in higher Reynolds numbers.
Transitional Flow and Its Challenges
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Even in the best CFD substrates today also unable to represent this transitional flow.
Detailed Explanation
Transitional flow occurs between laminar and turbulent phases and is characterized by changing flow patterns that are complex and challenging to model. While laminar flow is predictable, and turbulent flow can often be modeled using turbulence models, transitional flow exhibits a mix of both properties. It does not have a clear pattern, making it difficult for Computational Fluid Dynamics (CFD) simulations to accurately predict its behavior. Engineers often avoid transitional zones in designs due to this unpredictability.
Examples & Analogies
Consider a car speeding up on a straight road. Initially, the air flows smoothly over the car (laminar), but as it picks up speed, the airflow becomes turbulent around the car’s body. If you were to suddenly change speed or direction, the airflow might fluctuate wildly, representing transitional flow—a scenario that can't be easily predicted or modeled accurately.
Effect of Reynolds Number on Boundary Layer Thickness
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Higher the Reynolds number, thinner the boundary layers.
Detailed Explanation
The boundary layer thickness is inversely related to the Reynolds number: as the Reynolds number increases, the boundary layer becomes thinner. This is because, at higher Reynolds numbers, inertial forces overcome viscous forces, resulting in less fluid interaction and mixing near the boundary. Thus, with lower interaction, the region where the fluid velocity transitions from zero (at the boundary) to nearly the free stream velocity becomes narrower.
Examples & Analogies
Imagine spraying water from a hose. If you increase the water pressure (analogous to a higher Reynolds number), the stream narrows and flows faster and straighter. However, if you were to let the pressure drop, the flow would spread out more widely, similar to how a lower Reynolds number creates a thicker boundary layer.
Applications of Boundary Layer Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Boundary layer formations can be considered in many situations like wake formations behind a boat.
Detailed Explanation
Boundary layers are essential in various engineering applications, from aerodynamic designs to optimizing fluid flow in pipelines. For example, the wake behind a moving object, like a boat, behaves similarly to boundary layers, indicating how fluid flows in real-world conditions. Understanding how these layers form helps engineers design vehicles that minimize drag and enhance performance.
Examples & Analogies
Think about how a boat moves through water. The water that sticks to the boat's hull moves slower than the free-flowing water because of the boundary layer effect. The wake that trails behind the boat shows the turbulence created by the boundary layers, affecting how efficiently the boat travels through the water.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Number: Critical for determining flow type based on forces.
-
Laminar Flow: Occurs at Re < 100,000, characterized by smooth flow.
-
Transitional Flow: Zone of instability between laminar and turbulent.
-
Turbulent Flow: Occurs at Re > 3,000,000, characterized by chaotic motion.
-
Boundary Layer: Thin region affected by viscosity adjacent to surfaces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
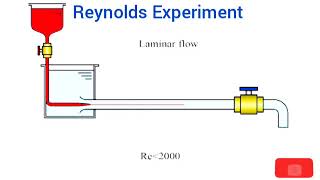
A flow of oil in a pipe might have a Reynolds number of 2000, indicating laminar flow, while air flowing past an airplane wing could exceed 1,000,000, leading to turbulence.
-
Experiments in a wind tunnel involving a flat plate can illustrate how flow transitions from laminar to turbulent as the velocity increases beyond critical Reynolds numbers.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Reynolds up high means chaotic flow; Down below, smooth as a gentle show.
📖 Fascinating Stories
-
Imagine a calm river flowing in layers by the shore; then a storm brews, and the water swirls, every core!
🧠 Other Memory Gems
-
Re = 100K (laminar), 3M (turbulent) - Use 100K for calm times, 3M for chaos in flow lines.
🎯 Super Acronyms
RLT
- Reynolds (Re) Lags Turbulence (T) - Helps remember the flow transitions!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reynolds Number
Definition:
A dimensionless number used to predict flow patterns in different fluid flow situations, defined as the ratio of inertial forces to viscous forces.
-
Term: Laminar Flow
Definition:
Type of flow characterized by smooth and orderly fluid motion, typically observed at Reynolds numbers less than 100,000.
-
Term: Turbulent Flow
Definition:
Type of flow marked by chaotic changes in pressure and flow velocity, occurring at Reynolds numbers greater than 3,000,000.
-
Term: Transitional Flow
Definition:
Type of flow existing between laminar and turbulent phases, generally occurring between Reynolds numbers of 100,000 and 3,000,000.
-
Term: Boundary Layer
Definition:
The thin region of fluid in immediate contact with a surface where the flow velocity changes from zero at the surface to the free stream velocity.