Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Velocity Distributions
Unlock Audio Lesson
Today we'll start with the concept of velocity distributions in laminar and turbulent flows. Why do you think understanding these distributions is important in fluid mechanics?
I think it helps us understand how fluids behave in different conditions.
Exactly! The behavior of fluids affects many real-world applications. Let’s dive into how we derive wall shear stress from the Navier-Stokes equations. What do you remember about these equations?
They describe how the velocity field of a fluid evolves with time.
Correct! They are fundamental in fluid dynamics. We can assume a system of parallel plates and calculate shear stress based on the flow's velocity. Imagine this setup: Can you visualize how the velocity varies from the center line to the walls?
Yes, I can see that the velocity decreases to zero at the walls due to the no-slip condition.
Great observation! This decrease is what we'll need to compute wall shear stress.
Understanding Wall Shear Stress
Unlock Audio Lesson
Let’s calculate wall shear stress. What expression can we use related to viscosity?
Is it something like τ = μ (du/dy)?
Correct! Here, μ is the dynamic viscosity and du/dy is the velocity gradient. Can anyone explain why this relationship highlights the importance of viscosity in fluid flow?
Because it shows how resistance to flow is influenced by the fluid's thickness.
Exactly! Now, how does this wall shear stress apply to our velocity fields under laminar conditions?
It helps us determine the rate at which momentum is transferred in our fluid layers.
Stream Functions and Vorticity
Unlock Audio Lesson
Next, we will examine stream functions. How do you think they relate to the velocity fields we've been discussing?
Stream functions can represent the flow patterns in a 2D plane.
Right! By integrating our u component, we can get the stream function. What does vorticity add to our understanding of these flows?
It tells us about the rotation of fluid elements, especially in turbulent flows.
Perfect! If the vorticity vector is not zero, what does that imply about our flow?
It suggests that the flow is not irrotational.
Exactly! This will directly impact our ability to find velocity potential functions.
Reynolds Number and Boundary Layers
Unlock Audio Lesson
Now let’s discuss the Reynolds number. Why is it a critical factor in fluid mechanics?
It determines if flow will be laminar or turbulent.
Correct! As we increase the Reynolds number, what happens to our boundary layers?
They become thinner.
Excellent! Can anyone relate this to the practical applications we discussed earlier?
In designing vehicles, understanding the boundary layer is important to minimize drag.
Exactly! This awareness allows engineers to optimize shapes to reduce resistance.
Velocity Distributions in Practice
Unlock Audio Lesson
Finally, let's apply what we've learned today to real-life situations. How would you evaluate the flow past a flat plate?
We would need to establish the velocity profile and use the appropriate Reynolds number.
Good! How would we calculate the average velocity in this context?
By integrating the velocity across the area and dividing by the area.
Excellent! This comprehensive view aids engineers in making informed design choices, concluding today’s session.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
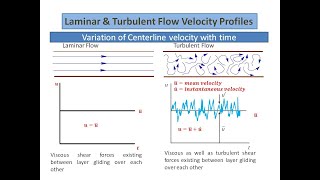
The section delves into the behavior of laminar and turbulent flows, detailing how to compute wall shear stress and velocity distributions. Key aspects like stream functions, vorticity, and velocity potential functions are introduced along with their implications in fluid dynamics.
Detailed
In this section, we explore velocity distributions in laminar and turbulent flows. The discussion begins with deriving wall shear stress from the Navier-Stokes equations, highlighting the simplified assumptions made (e.g., neglecting gravity). We then move on to examine how wall shear stress calculations relate to the fluid’s kinematics through partial derivatives. The section introduces concepts such as shear stress, pressure gradients, and how these contribute to establishing a velocity field under laminar conditions, primarily focusing on the parallel flow between two plates. We also touch on vorticity and discuss the limitations of velocity potential functions in irrotational flow scenarios. Additionally, the phenomenon of boundary layers and their characteristics in flow dynamics is introduced, emphasizing the significance of Reynolds numbers in distinguishing between laminar and turbulent regimes.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Flow Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Today we are looking at what will be the wall stress, shear stress at this point, also this point, stream function, vorticity, velocity potential and the average velocity if known the velocity field.
Detailed Explanation
In this chunk, we're introduced to several important concepts in fluid mechanics related to how fluids behave when they flow. Specifically, we focus on wall stress (force exerted by the fluid on the wall), shear stress (resistance of the fluid to flow), stream functions (which help describe flow patterns), and vorticity (the measure of rotation in the fluid). Understanding these concepts is crucial for analyzing both laminar (smooth) and turbulent (chaotic) flow.
Examples & Analogies
Think of a river as it flows past a bank. The interaction of the water with the bank involves wall stress, and depending on how fast the water flows (like a gentle stream vs. a rapid current), the characteristics such as shear stress and vorticity change. This helps us understand how rivers shape their banks over time.
Deriving Velocity Field from Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the last class, we estimated this velocity field from Navier-Stokes equations that we assume it vw is a 0 okay, neglecting the gravity force components. We get this u component...
Detailed Explanation
This segment explains how the velocity field is computed using the Navier-Stokes equations, which describe how fluid substances move. By neglecting certain forces (like gravity) and focusing on specific components of velocity (like 'u'), we can derive an expression for velocity that takes into account changes in pressure.
Examples & Analogies
Imagine water flowing through a narrow pipe: by applying the rules of flow (like the Navier-Stokes equations), you can predict how fast the water will go at different points, even if at first glance it seems chaotic.
Wall Shear Stress Calculations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it I am just substituting wall shear stress using the Newton's laws of viscosity...
Detailed Explanation
In this section, the speaker discusses calculating wall shear stress using Newton's laws of viscosity. This involves determining how much the fluid's velocity changes as it approaches the wall, which helps understand the frictional forces at work in fluid flow.
Examples & Analogies
Consider spreading butter on bread: the way the butter moves and slightly changes shape due to the pressure of the knife is similar to how fluid layers slide past each other due to shear stress.
Understanding Stream Function and Vorticity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since it is a 2-dimensional flow, we can get the stream functions...
Detailed Explanation
Stream functions simplify the analysis of flow by providing a way to visualize and calculate fluid flow patterns, especially in 2-dimensional scenarios. Vorticity pertains to the local spinning motion of the fluid, and understanding both these concepts is key to grasping fluid behavior in various flows.
Examples & Analogies
Imagine looking at a spinning top; the speed at which it spins represents vorticity. Likewise, stream functions can be seen as pathways that show us the direction the top would be thrown if we pushed it in various directions.
Velocity Potential Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We cannot get the velocity potential functions because to get a velocity potential function flow should be irrotational.
Detailed Explanation
Velocity potential functions can only be defined for irrotational flows, meaning that there is no rotation in the fluid's movement. This section explains that, because the flows being discussed are not irrotational (due to vorticity), we cannot derive a velocity potential function.
Examples & Analogies
Think of calm water in a pond. If you stir the water, it becomes rotational (swirling). The calm state represents irrotational flow, where a velocity potential could exist. Once stirred, that potential state is lost.
Average Velocity Computation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
You have to compute the average velocity... I will get it integrations over this.
Detailed Explanation
Here, the average velocity is computed by integrating flow velocities over a cross-sectional area, which provides a comprehensive view of flow behavior across different sections of the fluid body.
Examples & Analogies
Think about averaging your speed over a long road trip. Some parts of the trip you may drive faster, while in others, you might slow down. Calculating your average speed gives a better idea of your overall journey than simply looking at one aspect.
Summary of Application of Fluid Mechanics Principles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We try to get it what will be the average velocity, what will be wall shear stress, what will be the stream functions...
Detailed Explanation
In this concluding part, the speaker summarizes how all the discussed concepts come together to provide a holistic view of fluid motion. Each principle plays a role in understanding the complete flow dynamics, whether it is shear stress, stream functions, or average velocity.
Examples & Analogies
Imagine being a chef making a sauce. Each ingredient (like flavors from spices, thickness from butter, and tang from tomatoes) impacts the final dish. Similarly, understanding each fluid mechanic concept helps us see the complete 'dish' of fluid dynamics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Wall shear stress: The force exerted by fluid causing tangential motion against boundaries.
-
Stream function: A function that helps visualize flow patterns in two dimensions.
-
Vorticity: Measures rotation in fluid elements, crucial for understanding turbulence.
-
Reynolds number: A key factor in predicting flow behavior as laminar or turbulent.
-
Boundary layer: The region near a wall where viscous effects significantly modify the flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating wall shear stress using the equation τ = μ(dU/dy) from the velocity profile.
-
Visualizing stream functions to determine flow paths around objects.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When flows change their nature, here's the plot, Reynolds number's the key, connecting the dots.
📖 Fascinating Stories
-
Imagine a fluid racing past a surface; it slows down at the wall making a boundary layer—this is where shear stress starts to play its role.
🧠 Other Memory Gems
-
Remember VSB for Velocity, Shear stress, and Boundary layer: these are key concepts in flow analysis.
🎯 Super Acronyms
Use the acronym RBS for Reynolds, Boundary layer, and Shear stress to remember the fundamental aspects of flow.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Distribution
Definition:
The variation of fluid velocity in a flow field as a function of spatial coordinates.
-
Term: Wall Shear Stress
Definition:
The tangential force per unit area exerted by the fluid on a wall, influenced by viscosity and velocity gradients.
-
Term: Stream Function
Definition:
A mathematical function used to describe the flow of incompressible fluids, which associates with the flow velocity.
-
Term: Vorticity
Definition:
A measure of the local rotation in a fluid flow, represented by the curl of the velocity field.
-
Term: Reynolds Number
Definition:
A dimensionless quantity that predicts flow patterns in different fluid flow situations.
-
Term: Boundary Layer
Definition:
The thin region adjacent to a surface where viscosity dominates the flow behavior.