Reynolds Number and Boundary Layer Thickness
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Reynolds Number
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome, class! Today we are discussing Reynolds number, which is a critical concept in fluid dynamics. Can anyone tell me what Reynolds number helps us determine?

Is it to check if the flow is laminar or turbulent?

Exactly! The Reynolds number helps us understand the nature of fluid flow. It is defined as the ratio of inertial forces to viscous forces. Does anyone want to share the formula?

I think it's Re = U * L / µ, where U is the flow velocity, L is the characteristic length, and µ is the dynamic viscosity.

Well done! Understanding this ratio helps us determine whether the flow will remain smooth or become chaotic, based on the value of the Reynolds number.

So if Re is low, we expect laminar flow, right?

That’s correct! Conversely, a high Reynolds number indicates turbulent flow, which can be more complex and harder to predict. Remember, Re also influences the boundary layer characteristics.

How does the Reynolds number influence the boundary layer?

Great question! We'll dive into that shortly, but remember: as the Reynolds number increases, the boundary layer tends to become thinner because inertia overcomes viscosity more significantly.

In summary, Reynolds number plays a vital role in determining fluid behavior, especially in the context of boundary layers.
Boundary Layer Thickness Defined
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss boundary layer thickness. When we say boundary layer thickness, what exactly does that mean?

Is it the thickness of the layer where viscosity matters?

Exactly! The boundary layer is the region right next to the surface where viscous effects are significant. We define its thickness at the point where the flow velocity reaches 99% of the free-stream velocity. Can anyone calculate the notional thickness given this is conceptually?

So, if we have a flat plate and the velocity at the surface is zero and it rises to nearly the free-stream value, then... it would typically be calculated based on flow conditions?

That’s correct! The boundary layer thickness varies along the plate's length as characteristics of the flow change. It's essential for analyzing drag and lift forces.

And as the Reynolds number increases, the thickness decreases, right?

Smart observation! That's why we often deal with these thickness effects in fluid designs. Let’s hold this thought—next, we'll link boundary layer behavior with Reynolds numbers.

To summarize, the boundary layer is vital in flow analysis, significantly impacting performance in engineering applications.
Applications and Importance
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's connect these ideas to real-world applications. Why do engineers care about Reynolds number and boundary layer thickness?

It helps predict drag and lift forces on vehicles or aircraft!

Absolutely! For instance, if we design an aircraft wing, understanding the boundary layer can help minimize drag and maximize lift. What happens during transitions between laminar and turbulent flow?

The critical Reynolds number helps determine when those transitions occur.

You got it! Typically around 1,00,000 for many flows, while turbulent conditions start around 3,000,000. Recognizing these thresholds allows better control over fluid dynamics.

Does this mean we can manipulate designs to stay away from transitional flow to minimize body drag?

Exactly! Such strategies include using trip wires for inducing earlier transitions. In summary, these concepts guide us in designing systems to optimize performance based on flow behavior.
Visualizing Flow Patterns
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Visualizing fluid flow is key. What visualizations can we relate to boundary layers and Reynolds number?

We can draw streamlines showing how the fluid behaves near surfaces.

Right! Sketching streamlines helps illustrate how velocity changes from zero at the surface to the free-stream conditions. What would you expect the streamline pattern to look like for laminar vs. turbulent flow?

Laminar flow would have smoother, parallel lines, while turbulent would be a chaotic mix of lines.

Excellent distinction! This visualization allows us to comprehend the impact of the Reynolds number on flow behavior. Regular patterns signify predictability, while irregular patterns highlight turbulence.

And that’s crucial in many designs, ensuring we can anticipate forces acting on structures.

Absolutely! Visualizing these concepts leads to a clearer understanding of their practical applications. So recall these techniques as you tackle complex flow problems!

In summary, understanding the interaction between Reynolds number and boundary layers through visualization improves our ability to analyze and design effective systems.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section delves into Reynolds number, its role in determining flow regimes, and the concept of boundary layer thickness, explaining how it varies with Reynolds number and influences wall shear stress and flow behavior in both laminar and turbulent regimes.
Detailed
Reynolds Number and Boundary Layer Thickness
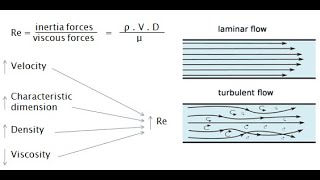
In this section, we explore Reynolds number, a crucial dimensionless parameter that characterizes the flow regime of fluids—determining whether the flow is laminar or turbulent. The Reynolds number is defined as the ratio of inertial forces to viscous forces, given by the formula:
\[ Re = \frac{U L}{bc} \]
where \( U \) is the flow velocity, \( L \) is a characteristic length, and \( \mu \) is the dynamic viscosity of the fluid. Understanding Reynolds number allows engineers and scientists to predict flow behavior in different scenarios, such as in piping systems or over surfaces.
The concept of boundary layer thickness describes the thin layer of fluid in immediate proximity to a surface where viscous effects are significant. As fluid flows over a flat plate, the velocity transitions from zero at the surface (due to no-slip conditions) to nearly free-stream velocity away from the surface. The boundary layer thickness \( \delta \) is defined at the point where the fluid velocity reaches 99% of the free-stream velocity.
Importance of Reynolds Number and Boundary Layer
The section highlights that lower Reynolds numbers indicate a laminar flow with smoother velocity profiles and thicker boundary layers, while higher Reynolds numbers signify turbulent flow, resulting in thinner boundary layers. Engineers must account for these factors to optimize designs. Additionally, flow transition points marked by critical Reynolds numbers (typically around 1,00,000 for laminar to turbulent transitions) can drastically affect drag and lift on surfaces, which is crucial in applications ranging from aerospace to civil engineering.
In closing, the relationship between Reynolds number and boundary layer thickness is essential for precise flow analysis and engineering applications.
Youtube Videos



![[Fluid Dynamics: Boundary layer theory] Turbulent Boundary Layer](https://img.youtube.com/vi/3NV5n2bUu0g/mqdefault.jpg)




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Boundary Layers
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The regions we call boundary layers are where vorticity and viscosity dominate. These regions are very thin compared to the overall flow domain, but they play a crucial role in determining shear stress on boundaries.
Detailed Explanation
Boundary layers form near surfaces when fluid flows over them, and the fluid closest to the surface does not move because of the no-slip condition. This means that the velocity of the fluid at the surface is zero. As we move away from the surface, the fluid eventually reaches the free-stream velocity. The region where this transition occurs is known as the boundary layer, which is typically very thin compared to the overall flow width.
Examples & Analogies
Imagine someone swimming in a pool. The swimmer's body creates ripples in the water; right next to the swimmer, the water is nearly still, but further away, the water is moving more freely. This 'calm' area next to the swimmer is akin to a boundary layer.
Reynolds Number and Its Significance
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Reynolds numbers help characterize the flow regime. They represent the ratio of inertia forces to viscous forces in fluid flow. For boundary layers, the critical Reynolds number defines the type of flow: laminar, transitional, or turbulent.
Detailed Explanation
The Reynolds number (Re) is a dimensionless quantity that indicates whether the flow is laminar (smooth and orderly) or turbulent (chaotic and irregular). It is computed using the equation Re = (v * L) / ν, where v is the velocity, L is the characteristic length (such as the length of a plate), and ν is the kinematic viscosity. In boundary layer theory, specific critical values of Reynolds number help predict whether the flow remains laminar or transitions to turbulence.
Examples & Analogies
Think of Reynolds number like a speedometer in a car. When you're driving slowly, the car is smooth and stable on the road (laminar flow). But if you speed up too quickly, the ride gets bumpy and chaotic, similar to turbulent flow behavior in fluids.
Boundary Layer Thickness
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Boundary layer thickness can be defined as the distance from the surface over which the fluid velocity reaches approximately 99% of the free-stream velocity. This thickness increases with the distance along the flow direction.
Detailed Explanation
The thickness of the boundary layer is a key parameter as it determines the region over which viscous effects are significant. It is defined by the point where the fluid velocity reaches 99% of the velocity of the fluid far from the surface. Usually, boundary layer thickness increases as you move downstream from the leading edge of the surface due to accumulation of the effects of viscosity.
Examples & Analogies
Consider a spray of water from a hose. Close to the nozzle, the water is forced out with a lot of energy and moving quickly. Right at the surface of whatever you are spraying, there's water that's barely moving. As you get away from the hose, the water is moving faster, if we plotted the speed, you could see how the thickness of the slower part (boundary layer) changes the further you go.
Flow Regimes in Boundary Layers
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Depending on the Reynolds number, boundary layers can be classified as laminar, transitional, or turbulent. Laminar flows are orderly, transitional flows show fluctuations, and turbulent flows are chaotic.
Detailed Explanation
The classification of flows into laminar, transitional, and turbulent depends on the Reynolds number. Laminar flow occurs at lower Reynolds numbers, where the flow is smooth and layered. As the number increases, the flow can transition into a transitional regime, which has some chaotic elements, and finally to turbulent flow, where swirls and eddies dominate and the flow is highly irregular and chaotic.
Examples & Analogies
Imagine traffic on a highway. At off-peak hours, cars move in an orderly fashion (laminar). As more cars enter the highway, you may see some start to weave in and out (transitional), and during rush hour, the traffic is continuously congested and chaotic (turbulent). This analogy reflects the smooth transition from laminar to turbulent flow in boundary layers.
Key Concepts
-
Reynolds Number: A dimensionless figure influencing fluid dynamics, where low numbers indicate laminar flow and high numbers indicate turbulent flow.
-
Boundary Layer: A thin region near a surface where shear stress affects the flow, defined by the point reaching 99% of the free stream velocity.
-
Critical Reynolds Number: The point at which fluid flow transitions from laminar to turbulent.
-
Inertia vs. Viscosity: In high Reynolds scenarios, inertial forces dominate over the viscous forces, particularly in turbulent flows.
Examples & Applications
When water flows gently around a flat plate at low speeds, flow is laminar and characterized by a thick boundary layer. As speed increases, flow transitions to turbulent, resulting in a thinner boundary layer.
In an aircraft wing design, managing the shear stress at the boundaries is crucial; engineers use knowledge of Reynolds numbers to optimize wing shape and thickness to minimize drag.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In fluid flow that's fast and grand, thick layers are hard to withstand. A lower Re means smooth and nice; a high one’s chaotic, like a spinning dice.
Stories
Imagine a car speeding on a highway. At low speed, the air glides smoothly (laminar); at high speed, it swirls and roars (turbulent). The thickness on the sides varies, just like our boundary layers.
Memory Tools
R-B-T: Remember B for Boundary, T for Thickness, and R for the Ratio of forces in Reynolds number.
Acronyms
R.E.B.L. - Reynolds number, Effects on Boundary Layer.
Flash Cards
Glossary
- Reynolds Number
A dimensionless quantity that helps predict flow patterns in fluid dynamics, calculated as the ratio of inertial to viscous forces.
- Boundary Layer Thickness
The distance from a surface to a point in the fluid where the velocity reaches 99% of the free-stream velocity, crucial for understanding viscous effects.
- Laminar Flow
A smooth, orderly flow regime characterized by parallel streamlines and low Reynolds number.
- Turbulent Flow
A chaotic flow regime characterized by mixing and irregularities, typically occurring at high Reynolds numbers.
- Critical Reynolds Number
The specific Reynolds number value at which flow transitions from laminar to turbulent.
Reference links
Supplementary resources to enhance your learning experience.
