Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Flow States
Unlock Audio Lesson
Today, we're diving into flow transitions! Can anyone explain what laminar flow is?
Isn’t it when the fluid moves in parallel layers without disruption?
Exactly! Laminar flow is all about smooth, orderly motion. Now, can you describe turbulent flow?
That’s when the flow becomes chaotic, right? Like water swirling around?
Precisely! The disorder in turbulent flow contrasts with laminar flow. What do we think happens at intermediate points?
That’s the transitional flow, where it switches from one state to another!
Yes, great job! Let's summarize these key concepts: Laminar is smooth, turbulent is chaotic, and transitional is the in-between state.
Understanding Boundary Layers
Unlock Audio Lesson
Next, let’s talk about boundary layers. What do you think they are?
They must be the thin layers where viscous effects are significant!
Correct! They form near surfaces due to no-slip conditions. What does this imply for the flow above them?
The flow is smoother above the boundary layer?
Yes! The outer flow can be approximated as inviscid. Knowing this helps in using simpler equations like Euler's. Can someone explain the significance of Reynolds number here?
Reynolds number relates the inertial forces to viscous forces, showing when laminar flow transitions to turbulent!
Well said! Remember, a low Reynolds number indicates laminar flow, while high values signal turbulence. It’s crucial for predicting these transitions.
Reynolds Number and Flow Transitions
Unlock Audio Lesson
We’ve mentioned Reynolds numbers. What are the critical numbers distinguishing laminar, transitional, and turbulent flows?
Is it less than 100,000 for laminar, and greater than 3 million for turbulent?
Exactly! The region in between is transitional, which can be quite complex. Can anyone think of how we might manage these transitions in engineering?
Using trip wires to create turbulence quickly and avoid unwanted mixed flow areas?
Spot on! Trip wires disturb the flow to push it toward the turbulent state, enhancing stability. Can anyone summarize why understanding these transitions is critical?
It’s essential for designing efficient systems in engineering and analyzing fluid behaviors.
Great summary! Always remember that knowledge of boundary layers and flow states is vital in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses fluid dynamics by examining the transitions between laminar and turbulent flow states. It emphasizes the role of boundary layers, the critical Reynolds numbers that distinguish these states, and the methods used to analyze the flow, including the Navier-Stokes equations and boundary layer approximations.
Detailed
Detailed Summary
In this section, we delve into the transitional flow states in fluid dynamics, focusing on the transition from laminar to turbulent states. Laminar flow is characterized by smooth, orderly fluid motion, which transitions to the chaotic and irregular motion found in turbulent flow.
The concept of boundary layers plays a critical role in understanding these transitions. A boundary layer forms when a fluid flows over a surface, leading to regions where viscosity is significant. A key insight is that the Reynolds number serves as a dimensionless metric to predict flow behavior:
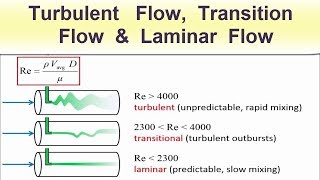
- A Reynolds number lower than 100,000 indicates laminar flow.
- Values above 3,000,000 lead to turbulent flow.
- The zone between these figures is transitional, where flow experiences complex dynamics, making it challenging to predict and analyze.
The analysis framework includes using Navier-Stokes equations to describe fluid motion and shear stresses. The complexity is compounded in transitional zones, where mixed behaviors occur, necessitating approximations for practical computation, often leveraging tools like Computational Fluid Dynamics (CFD). Additionally, the concept of trip wires is introduced as a practical solution to manage transitions, facilitating a smoother flow and suppressing unwanted effects during the transit between laminar and turbulent states.
Understanding these transitions and their implications for fluid properties is essential in various engineering and environmental applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Flow Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Two-dimensional flow, incompressible, Newtonian fluid. So that is what I am repeating it to tell it that fluid flow problems are not easy. You simplified it for a specific cases to get some solutions.
Detailed Explanation
This chunk emphasizes the nature of fluid flow in relation to dimensionality, compressibility, and fluid type. In fluid dynamics, we often categorize flows based on their characteristics: two-dimensional, incompressible, and Newtonian. Two-dimensional flow refers to flow patterns where the velocity can be described using two spatial dimensions. Incompressible flow means the fluid density remains constant throughout the flow. Newtonian fluids follow Newton's law of viscosity, meaning the relationship between shear stress and shear rate is linear. Recognizing these distinctions helps simplify complex fluid problems into manageable forms.
Examples & Analogies
Think of riding a bicycle through still water. The way the bike moves through the water can be viewed as two-dimensional flow—the direction you're biking and the path beneath the tires can be plotted on a flat surface. The water does not compress and its behavior can be predicted similarly to how we understand air's flow around a moving object, like a car.
Boundary Layer Formation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As we look at this way that we have had 2 tanks the liquids are there and the liquid is coming from tank 1 supplying tank to the receiving tank if it is happening that. See if you look at when fluid flow is coming it that is what we have to understand it.
Detailed Explanation
In this section, a scenario is presented involving two tanks connected by a pipe, where fluid flows from one to the other. The principle of boundary layers is particularly relevant here. A boundary layer forms when fluid moves close to a surface, creating a region where velocity changes from that of the surface (zero at the wall due to no-slip condition) to the free stream velocity. This layer is crucial for understanding shear stress and flow behavior near surfaces, influencing drag and lift in applications like vehicles and airplanes.
Examples & Analogies
Imagine a river flowing over rocks. Close to the rocks, the water speed is slower due to friction (akin to the no-slip condition). As you move away from the rocks, the water speeds up, creating layers of flow speed. This concept is similar to how the boundary layer forms in liquids flowing past surfaces.
Vorticity and Shear Stress
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So now if you look it I am just substituting wall shear stress using the Newton's laws of viscosity we can get tau xy wall fluid kinematics.
Detailed Explanation
The wall shear stress is a critical factor in fluid dynamics, governed by Newton's laws of viscosity. Shear stress (τ) relates to how fluid velocity changes across a boundary (the wall), expressed mathematically through partial derivatives of the velocity field. Understanding how wall shear stress behaves allows engineers to predict how fluids interact with surfaces, which is essential for designs in transportation and machinery.
Examples & Analogies
Think of spreading butter on bread. As you push the knife (representing the wall) against the butter, it resists movement (this resistance is comparable to shear stress) because the butter (fluid) sticks to both the knife and the bread. The rate at which the butter spreads reflects how viscosity impacts the shear stress at the boundary.
Critical Reynolds Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Reynolds numbers is 1 lakh okay we see easy to remember 1 is to 10 to the power 5. So in case of Reynolds numbers if it is lesser than that critical Reynolds number lesser than 1 lakh 1 is to 10 to the power 5 okay 1 lakh 1 is to 10 to the power 5 if a Reynolds numbers lesser than these this is a critical Reynolds numbers. then flow is laminar.
Detailed Explanation
The Reynolds number is a dimensionless quantity used to predict flow patterns in different fluid flow situations. The critical Reynolds number helps to distinguish between laminar and turbulent flow. If the Reynolds number is less than approximately 100,000, the flow is generally stable and laminar. Conversely, if it exceeds 3,000,000, the flow becomes chaotic and turbulent. This transition affects how fluids behave under various conditions and is vital in engineering applications involving fluid dynamics.
Examples & Analogies
Consider a school hallway. When a small number of students are walking quietly, their movement can be thought of as laminar flow—organised and calm. However, when the bell rings and everyone rushes out, the chaos represents turbulent flow. The number of students in the hall at one time is analogous to the Reynolds number—the higher it goes, the more chaotic the flow becomes.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Identifying Laminar Flow: Characterized by smooth, parallel motion.
-
Understanding Turbulent Flow: Chaotic motion with eddies and vortices.
-
Recognizing Transitional Flow: The uncertain state between laminar and turbulent.
-
Boundary Layer Formation: Layers adjacent to surfaces where viscosity dominates.
-
Critical Reynolds Numbers: Key thresholds for flow states.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a smooth pipe, water flows in a laminar manner when Reynolds number is below 2,300.
-
A river exhibits turbulent flow as it cascades over rocks, characterized by irregular motion.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Smooth and straight, laminar is great;
📖 Fascinating Stories
-
Imagine a calm lake, rippling gently. Suddenly, wind stirs up the water, creating waves—the calm turns chaotic, just like laminar turning turbulent.
🧠 Other Memory Gems
-
Remember LTT: Laminar, Transitional, Turbulent. The flow states in order!
🎯 Super Acronyms
Use **R-LT** to remember Reynolds for Laminar and Turbulent flow thresholds.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Laminar Flow
Definition:
A type of flow characterized by smooth, parallel layers of fluid with minimal disturbance.
-
Term: Turbulent Flow
Definition:
A chaotic flow regime characterized by eddies, vortices, and irregularities.
-
Term: Transitional Flow
Definition:
The flow regime that occurs between laminar and turbulent flow, displaying characteristics of both.
-
Term: Boundary Layer
Definition:
A thin region adjacent to a surface where viscous forces dominate and fluid motion interacts with the boundary.
-
Term: Reynolds Number
Definition:
A dimensionless number that expresses the ratio of inertial forces to viscous forces in a fluid flow.