Introduction to Boundary Layers
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Boundary Layers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're diving into the concept of boundary layers. Who can tell me what a boundary layer is?

Isn't it the region near a surface where viscosity affects the flow?

Exactly! Boundary layers are thin regions adjacent to surfaces where velocity gradients and viscous forces come into play. Can anyone think of an example where boundary layers are important?

When airflow passes over an airplane wing!

Correct! The boundary layer affects how lift is generated. Remember our acronym 'GLIDE' for remembering key factors affected by boundary layers: G for Gravity, L for Lift, I for Inertia, D for Drag, and E for Energy loss.

So, are the boundary layers thicker for slower moving fluids compared to faster ones?

Great observation! Higher Reynolds numbers often lead to thinner boundary layers due to increased inertial effects.

To summarize, boundary layers are key in understanding flow near surfaces, notably affecting lift and drag in aerodynamic applications.
Navier-Stokes Equations and Boundary Layers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s talk about the Navier-Stokes equations. How do they relate to boundary layers?

I think they help us understand how velocity fields and shear stress are determined?

That's right! The Navier-Stokes equations provide a framework for analyzing flows. In boundary layers, we must consider the no-slip condition, which governs the flow velocity at the wall.

What happens if the flow is turbulent?

In turbulent flow, boundary layers are complex, exhibiting significant mixing and energy losses. The transition from laminar to turbulent flow typically occurs at a certain Reynolds number, around 1 lakh for flat plates.

Is that why designing smooth surfaces is crucial for aircraft?

Absolutely! The smoother surfaces help maintain a laminar boundary layer longer, reducing drag. Remember the term 'smooth surfaces, easy flows' as a mnemonic!

To wrap up, the Navier-Stokes equations are fundamental in fluid mechanics, especially in analyzing the effects of viscosity in boundary layers.
Reynolds Number and Flow Types
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s discuss Reynolds number. What does it tell us about flow?

It helps us identify whether the flow is laminar or turbulent?

Exactly! A Reynolds number below 1 lakh indicates laminar flow, while above 3 million usually signifies turbulent flow. Can someone summarize why knowing this is important?

It affects how we analyze fluid mechanics problems, especially in computing drag and lift.

Well done! And remember, flow in between is transitional, often leading to complex behaviors.

In conclusion, the Reynolds number is a critical non-dimensional parameter in fluid mechanics for identifying flow regimes.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Boundary layers are critical in understanding fluid flow, particularly in regions near surfaces where viscosity and velocity gradients dominate. This section discusses the formation of boundary layers, their characteristics, and the mathematical tools used to analyze them, particularly in the context of the Navier-Stokes equations.
Detailed
Boundary layers are thin regions adjacent to surfaces in flowing fluids where the effects of viscosity are pronounced. They arise due to the no-slip condition at solid boundaries, resulting in velocity gradients that lead to shear stresses on the surfaces. This section elaborates on the mathematical framework used to analyze these layers, primarily through the Navier-Stokes equations. It differentiates between laminar and turbulent boundary layers, emphasizing the Reynolds number's importance in determining flow behavior. Additionally, it discusses how boundary layers affect drag and lift forces on objects in flow and introduces the approximations that simplify complex flow analysis.
Youtube Videos



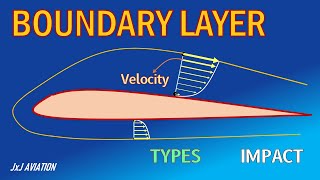



![[Fluid Dynamics: Boundary layer theory] Turbulent Boundary Layer](https://img.youtube.com/vi/3NV5n2bUu0g/mqdefault.jpg)

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Wall Stress and Shear Stress
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Today we are looking at what will be the wall stress, shear stress at this point, also this point...
Detailed Explanation
In fluid mechanics, when fluid flows over a surface, it exerts a force on that surface, which is referred to as 'stress'. Specifically, 'wall stress' or 'shear stress' is crucial for understanding how fluids interact with surfaces. The wall shear stress is calculated using Newton's law of viscosity, which relates shear stress (τ) to the velocity gradient near the wall. Here, shear stress can be expressed as τ = μ(dU/dy), where μ is the dynamic viscosity, U is the fluid velocity, and y is the distance from the wall. Thus, understanding shear stress helps in analyzing the behavior of fluid flows near surfaces.
Examples & Analogies
Imagine sliding your hand across a smooth table. The resistance you feel is similar to shear stress. Just as the texture of the table influences how much resistance you feel (akin to the viscosity of a fluid), the properties of the fluid and the surface will change the stress exerted at the wall when fluid flows over it.
Velocity Field and Pressure Gradient
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We estimate this velocity field from Navier-Stokes equations that we assume it vw is a 0, neglecting the gravity force components...
Detailed Explanation
To comprehensively analyze fluid flow, we utilize the Navier-Stokes equations—fundamental equations in fluid dynamics that describe how the velocity field of the fluid is influenced by internal and external forces. The assumption vw = 0 simplifies our calculations, allowing us to neglect gravitational effects and focus solely on the pressure gradient. The results yield a function expressing velocity in terms of pressure gradient, which provides critical insights into flow behavior between two fixed surfaces.
Examples & Analogies
Think of a river flowing between two banks. If we ignore wind and other forces, the river’s velocity is dictated by the water's slope (pressure gradient) and how fast the water is pushed forward. Just like in our equation, if we know the slope, we can predict how quickly the water flows.
Stream Function and Flow Characteristics
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look at the flow on a plane, it is a 2 dimensional plane flow that is what so it can have the stream flow...
Detailed Explanation
In two-dimensional flow fields, we can define a 'stream function' that aids in visualizing flow patterns. The stream function is a mathematical tool that helps depict how fluid continues to move in a flow field without directly measuring velocity. For a steady, incompressible flow, the stream function is particularly useful as it leads to constant flow lines, allowing us to better understand patterns and velocities across the field.
Examples & Analogies
Imagine a crowded subway station where commuters move along designated paths. The 'stream function' is like the paths or lines along which the commuters prefer to flow, helping to predict where most people will be at any given time based on their intended destinations.
Vorticity and Velocity Potential Functions
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If vorticity vector could be 0 we could compute the velocity potential functions...
Detailed Explanation
Vorticity provides a measure of rotational components of flow. In irrotational flow (where vorticity is zero), we can derive a 'velocity potential function' that simplifies the analysis of fluid movement. However, if vorticity is present (as in most real-world flows), potential functions cannot be computed accurately, complicating the analysis and requiring more advanced approaches.
Examples & Analogies
Think of a spiral staircase. If someone were to run straight up (irrotational), their path could easily be predicted. But if they sprint randomly around the staircase (rotational), predicting where they will end up becomes complicated.
Boundary Layers – Formation and Significance
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
There will be regions where we have the boundary layers. These are the regions where we have the boundary layers...
Detailed Explanation
Boundary layers form in regions close to walls where viscosity affects flow significantly. As fluid particles come into contact with a surface, the flow velocity decreases due to friction (no-slip condition). This results in a thin zone (boundary layer) where flow characteristics differ from the main flow, which is critical to understanding drag and lift forces in applications like aircraft and vehicle design.
Examples & Analogies
Think of a swimmer in a pool. As they swim, the water closest to their body (boundary layer) is affected by their motion and slows down due to friction, while the water further away (main flow) remains relatively undisturbed. The swimmer must push against both layers, but the drag felt is mainly influenced by that boundary layer.
Reynolds Number and Flow States
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Here also we define the Reynolds number considering the characteristic length in x direction...
Detailed Explanation
The Reynolds number (Re) is a crucial dimensionless quantity in fluid mechanics, defined as the ratio of inertial forces to viscous forces. It helps predict flow patterns: laminar, transitional, or turbulent. Generally, for Re < 100,000, flow remains laminar, while for Re > 3,000,000, turbulence dominates. Understanding where a flow falls on this scale is critical for predicting behavior and optimizing designs in fluid systems.
Examples & Analogies
Imagine riding a bike. If you ride slowly, it's easy to keep your balance (laminar flow), but if you speed up too much, the wind pushes against you, making it harder to control (turbulent flow). The Reynolds number helps scientists predict these transitions in fluid flows.
Key Concepts
-
Boundary Layer: The region where viscous effects dominate and affect flow characteristics.
-
Navier-Stokes Equations: Equations describing the motion of fluid substances.
-
Reynolds Number: A dimensionless quantity used to predict flow patterns.
Examples & Applications
A water jet flowing past a flat plate illustrating boundary layer formation.
Airflow over an airplane wing demonstrating the significance of boundary layers in lift generation.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In boundary layers, speed is low, where viscosity is sure to show!
Stories
Imagine a river flowing past smooth stones. Just like the water hugs the stone, the flow 'slows' down near the surface, creating a boundary layer.
Memory Tools
Remember 'BLAST' for boundary layer effects: B for Boundary location, L for Lift impacts, A for Area of surface, S for Shear stress, T for Turbulence effects.
Acronyms
Remember 'BRL' for Boundary Layer
for Boundary
for Reynolds number
for Lift.
Flash Cards
Glossary
- Boundary Layer
A thin layer adjacent to a surface where viscous effects dominate and velocity gradients exist.
- NavierStokes Equations
Fundamental equations describing fluid motion, taking into account viscosity.
- Reynolds Number
A dimensionless number indicating the ratio of inertial forces to viscous forces in a fluid flow.
- Laminar Flow
A flow regime characterized by smooth, orderly motion with minimal mixing.
- Turbulent Flow
A flow regime characterized by chaotic changes in pressure and flow velocity.
Reference links
Supplementary resources to enhance your learning experience.
