Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basic Concepts of Navier-Stokes Equations
Unlock Audio Lesson
Good morning, everyone. Today, we are diving into the Navier-Stokes equations. Can anyone tell me what these equations fundamentally represent in fluid mechanics?
Are they about how fluids move and behave under various forces?
Exactly! They describe the motion of fluid substances. The equations involve mass conservation and momentum conservation for fluids. Remember this acronym: 'M&M' for Mass and Momentum. Can anyone tell me how many equations are involved in this?
Four equations, right?
Correct! Now, what do we mean by incompressible flow?
It means the fluid density stays constant?
Right! That is a crucial assumption. This leads us to the idea that the divergence of the velocity field is zero. That's our first simplified form when dealing with incompressible fluids.
Approximations in Navier-Stokes Equations
Unlock Audio Lesson
Now that we understand the basics, let's talk about how we can approximate these equations for simpler analyses. Why do we need to simplify them?
Because real-world problems can get very complex?
Correct! We often see non-linear terms, especially in momentum equations. If certain terms can be neglected, we can derive the Euler equations. Who can explain the significance of those equations?
They describe the motion of an ideal fluid without viscosity.
Exactly! And under the right conditions, such as low viscosity or steady flows, we can simplify our equations significantly. There’s a helpful trick: if viscosity is closer to zero, we lean towards those Euler equations.
Boundary Conditions and Their Importance
Unlock Audio Lesson
Let's discuss boundary conditions, which are critical when applying fluid equations. What is a no-slip condition?
That’s when the fluid in contact with a surface has zero velocity relative to that surface.
Great! That ensures we properly account for how fluids interact with surfaces. Can anyone think of another boundary condition we often encounter?
The free surface condition between air and water?
Exactly! These boundaries help us define the scenarios under which we solve our equations accurately. Understanding these helps us derive solutions like Bernoulli's equation later on.
Simplified Fluid Flow Examples
Unlock Audio Lesson
To solidify our understanding, let's consider practical examples where these equations apply. Can someone share a real-world fluid scenario?
Blood flow in arteries.
Good example! As blood flows, we assume incompressibility. With certain conditions, we can ignore viscous effects, showing how simplifications come into play.
What about in rivers? Their flow can change with obstacles, right?
Exactly, which leads us to complex behaviors like vortex formation. Identifying whether these flows are symmetric or asymmetric helps guide how we apply our fluid equations.
Conclusion and Review
Unlock Audio Lesson
Today, we made considerable strides in understanding the Navier-Stokes equations and their approximations. Can anyone summarize how we simplified them?
By applying assumptions like incompressibility and ignoring viscosity under specific conditions.
Great, and what does this allow us to derive?
Equations like Bernoulli's that help us analyze fluid flow without too much complexity.
Exactly! Remember, the approximations simplify the overall analysis of fluid dynamics, which is crucial in engineering and real-world applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Navier-Stokes equations, crucial in fluid mechanics, can be approximated under certain assumptions, such as incompressibility and Newtonian behavior. This section highlights how neglecting specific terms and utilizing simpler forms, like the Euler equations, aids in understanding fluid behavior and deriving related equations like Bernoulli's.
Detailed
Detailed Summary of Approximations of Navier-Stokes Equations
The Navier-Stokes equations form the foundation for analyzing fluid motion, encompassing mass conservation and momentum equations that govern the movement of fluids. This section elaborates on how to approximate these equations to facilitate simpler analyses in specific conditions, particularly for incompressible Newtonian fluids.
Key assumptions include:
- Incompressibility: Fluid density is constant, leading to the simplification of the continuity equation. The mathematical representation confirms that the divergence of the velocity field is zero for incompressible flow.
- Newtonian Fluids: Viscosity is constant, crucial for establishing the linear momentum equations, allowing for analytical solutions due to the linear nature of these equations.
- Simplification Assumptions: Under certain scenarios, terms related to viscous stress and non-linear interactions may be negligible. For instance, when viscosity approaches zero, simplified equations such as the Euler equations emerge, which do not account for viscosity effects and thus describe ideal fluid flow.
- Boundary Conditions: The section also touches upon defining suitable boundary conditions such as no-slip and interface conditions, essential in solving fluid mechanics problems accurately.
Overall, the approximations of the Navier-Stokes equations not only simplify complex fluid behavior analysis but also serve as a precursor to deriving widely-used equations such as Bernoulli's equation.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Today I will talk about the Navier-Stokes equations, how we do the approximations of Navier-Stokes equations for a simplified fluid flow with a series of illustrations that how we can simplify these Navier-Stokes equations.
Detailed Explanation
The Navier-Stokes equations are fundamental in fluid mechanics, representing the motion of fluid substances. They consist of four equations that account for mass conservation and linear momentum. Because of their complexity, especially in real-world applications, approximations are needed. This section discusses how we can simplify these equations through various assumptions, facilitating easier calculations and analysis in fluid dynamics.
Examples & Analogies
Imagine a complex recipe with many ingredients and steps. Simplifying the recipe by focusing only on the main ingredients and basic steps (e.g., substituting ingredients or skipping non-essential steps) allows you to create a quick version of the dish while retaining its essence. Similarly, approximating the Navier-Stokes equations helps us solve fluid mechanics problems more easily without losing sight of key principles.
Continuity Equation for Incompressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
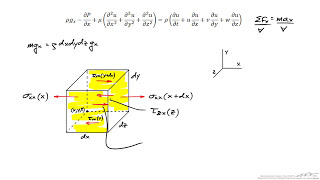
If you look at this Navier-Stokes equations which is in Cartesian coordinates if I can write in vector forms which is easy to remember it is del cross dot v divergence of velocity vectors is 0 for incompressible fluid flow and that is the equations of continuity equations.
Detailed Explanation
The continuity equation expresses the principle of mass conservation within a fluid flow. For incompressible flows, the density remains constant, which simplifies our calculations. The equation can be represented in vector form where the divergence of the velocity vector is equal to zero, indicating that the fluid's volume remains constant as it flows. This concept is fundamental in fluid dynamics, illustrating that the amount of fluid entering a region must equal the amount exiting, assuming no accumulation within that region.
Examples & Analogies
Think of water flowing through a garden hose. If you squeeze the hose (creating a constriction), the water flows faster through that narrowed section, but the total volume of water entering and exiting remains the same, illustrating the continuity principle. Just like how the hose maintains a constant volume flow rate, incompressible fluid flow obeys the continuity equation.
Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, if you look at the next the linear momentum equations as we have derived this is linear momentum equations in vector forms. So, in vector forms it comes like rho So, it is the accelerations part is equal to is rho g grade p pressures into mu Laplace operators of velocity field.
Detailed Explanation
The linear momentum equations describe how the motion of fluid particles changes under the influence of various forces such as pressure, gravitational pull, and viscous shear forces. The term 'rho' refers to fluid density, while the Laplace operator indicates how the velocity field varies within the fluid. Therefore, these equations help predict how fluids will behave under exerted forces, enhancing our understanding of fluid motion dynamics.
Examples & Analogies
Consider a car accelerating on a road. The car's acceleration (change in velocity) is influenced by forces like the engine's power (analogous to pressure), gravity (acting downhill), and friction (similar to viscosity). Likewise, the linear momentum equations help us quantify how fluids respond to similar forces at play within their environment.
Non-linear Terms in Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, if I write that equations in x directions I will get a local accelerations, the convective accelerations which will have non-linear terms, I will have a pressure gradient, the gravity force components.
Detailed Explanation
In fluid dynamics, non-linear terms arise due to the convective acceleration—movement of the fluid affects its velocity. This non-linearity complicates the solutions to the Navier-Stokes equations, as these terms involve products of the velocity components and their derivatives. Understanding these non-linear dynamics is crucial as they lead to complex flow behaviors such as turbulence, which are challenging to predict and control.
Examples & Analogies
Imagine a crowded subway train. The movement of passengers pushing and swaying creates complex interactions that are hard to predict. Similarly, in fluids, the non-linear interactions lead to unpredictability in flow patterns, especially when factors like turbulence come into play.
Reducing Complexity: The Euler Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, if these terms are 0 in a particular fluid flow, then these equations becomes a very linear form of very simplified equations that is what we called the Euler equations.
Detailed Explanation
The Euler equations simplify the Navier-Stokes equations by disregarding the effects of viscosity (when viscosity is much smaller or negligible) and focusing on inviscid flow. These equations allow for an analytical approach to fluid dynamics in idealized conditions where fluid does not experience resistance. Understanding when it is appropriate to apply these equations is key when analyzing flows where viscous effects are minimal.
Examples & Analogies
Think about swimming in a pool (viscous) versus swimming in a large lake (less viscous). When swimming in the lake, you feel less resistance from the water, and your strokes are more straightforward, similar to how the Euler equations simplify the analysis of fluid flow by ignoring viscosity.
Applications of Simplified Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we will try to simplify the equations to try to get analytical solutions for that. That is what the strategy.
Detailed Explanation
In fluid mechanics, simplifying equations such as the Navier-Stokes and approximating them through methods like the Euler equations enables engineers and scientists to derive analytical solutions for complex fluid behaviors. These simplifications facilitate understanding under ideal or constrained conditions where exact solutions would be cumbersome or not feasible.
Examples & Analogies
When planning a road trip, you can choose the most straightforward route using maps or GPS rather than tracking every possible detour considering every road condition. Similarly, in fluid dynamics, using simplified equations allows engineers to focus on the main aspects of fluid flow without getting lost in complexities.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Approximations: Under certain conditions, Navier-Stokes equations can be simplified to yield easier forms like the Euler equations.
-
Viscosity: The constant nature of viscosity in Newtonian fluids enables straightforward calculations in fluid mechanics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Blood flow in arteries can often be treated as incompressible and Newtonian, allowing simplifications of governing equations.
-
Water flow in a river can exhibit turbulence or laminar characteristics depending on environmental factors, impacting the applicability of the Navier-Stokes equations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluids flow like a breeze, Navier-Stokes answers our needs.
🧠 Other Memory Gems
-
Imagine a river flowing smoothly, where the water behaves like a well-behaved friend, standing still at the banks (no-slip), but moving freely in the stream (incompressible). It helps engineers design safe structures.
🧠 Other Memory Gems
-
NICE: Navier equations, Ideal fluids, Constant viscosity, Energy conservation.
🎯 Super Acronyms
M&M for Mass and Momentum; the foundation of our fluid equations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of equations that describe the motion of fluid substances. They encompass mass conservation and momentum equations.
-
Term: Incompressible Flow
Definition:
A flow condition where fluid density remains constant throughout.
-
Term: Newtonian Fluids
Definition:
Fluids that have a constant viscosity regardless of the flow conditions.
-
Term: Euler Equations
Definition:
Simplified fluid equations that neglect viscous forces, applicable in ideal conditions.
-
Term: NoSlip Condition
Definition:
A condition where the fluid velocity at a boundary is zero relative to that boundary.
-
Term: Bernoulli's Equation
Definition:
An equation that describes the conservation of energy in flowing fluids, derived under specific conditions.