Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Navier-Stokes Equations
Unlock Audio Lesson
Good morning, class! Today we will discuss the Navier-Stokes equations, which are crucial for modeling fluid motion. Can anyone tell me what components make up these equations?
They include mass conservation and momentum equations, right?
Great! Yes, mass conservation relates to the continuity equation, while momentum relates to the forces acting on the fluid. Remember the acronym 'M' for mass and 'F' for forces in Newton's second law. Can you tell me the assumptions we make for incompressible flu?
I think we assume constant density and viscosity.
Exactly! These assumptions simplify our equations significantly. Let's explore how we derive these equations next.
Approximations in Navier-Stokes Equations
Unlock Audio Lesson
Now, let’s talk about approximations. When might we simplify the Navier-Stokes equations?
I think when viscosity is negligible, we can use Euler's equations instead.
Absolutely! Viscosity plays a crucial role. When it's negligible, we derive Euler's equations. Can someone summarize what Euler's equations consist of?
They represent mass times acceleration being equal to force due to pressure and gravity.
Well done! Remember, under certain conditions, these equations simplify our computations greatly. Who can explain how this relates to computational fluid dynamics?
Computational Fluid Dynamics (CFD)
Unlock Audio Lesson
Let’s explore the role of Computational Fluid Dynamics. Why is it significant in our studies?
It helps in solving complex equations that we can't solve analytically.
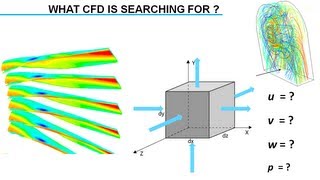
Correct! CFD allows for numerical approaches to determine approximate values for velocity, density, and pressure. How can we apply these methods in real-world scenarios?
We can study blood flow dynamics or even design tidal energy harvesters!
Excellent examples! Understanding these dynamics is vital for advancements in both engineering and health sciences.
Boundary Conditions and Flow Dynamics
Unlock Audio Lesson
Next, let’s discuss boundary conditions. How do they affect fluid flow?
They define how the fluid interacts with its surroundings.
Exactly! Conditions like no-slip at a surface and interface conditions between two fluids play key roles. Can anyone give me an example of such conditions?
An example would be the interface between water and air!
Right! The shear stress at the interface must be equal for both mediums. Great work class! Always remember, conditions are crucial in defining the behavior of fluid flow.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the Navier-Stokes equations for incompressible Newtonian fluids, exploring assumptions made during derivations, approximations for simplified flows, and the significance of computational fluid dynamics in finding solutions to complex flow problems.
Detailed
Detailed Summary
In this section, we delve into the fundamental aspects of the Navier-Stokes equations, which are the cornerstone for modeling fluid motion. The equations consist of mass conservation and momentum equations essential for understanding incompressible Newtonian fluids. We discuss the assumptions leading to these equations, including fluid incompressibility and constant viscosity, especially under isothermal conditions.
Key Equations and Concepts
The Navier-Stokes equations are presented in both vector form and Cartesian coordinates, allowing for a clearer understanding of continuity and linear momentum equations. The discussion also highlights the significance of approximations made under various flow conditions, enabling the simplification of complex equations into the Euler equations in scenarios where viscosity does not dominate the flow.
Role of Computational Fluid Dynamics (CFD)
Computational Fluid Dynamics plays a pivotal role in solving the Navier-Stokes equations numerically, especially for complicated cases which cannot be solved analytically. The section emphasizes how CFD methods approximate solutions to velocity, density, and pressure fields under various boundary conditions.
Finally, the importance of understanding flow dynamics, including both symmetric and asymmetric conditions, is stressed, expanding on real-world physiologic implications, such as blood flow in human arteries and tidal energy harvesting potential.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Computational Fluid Dynamics (CFD)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
No doubt, today we have a computational fluid dynamics with us. We can solve this equation. It is not that complex. As I discussed that we are doing for a very simplified cases like Newton fluid, incompressible, isothermal, also the laminar flow. But when you go for a very complex flow like turbulent flow, you talk about temperature changing, we can have another equations on energy conservation.
Detailed Explanation
Computational Fluid Dynamics (CFD) allows us to simulate fluid flow and solve the Navier-Stokes equations numerically. While CFD can help us with simple cases, like Newtonian, incompressible, and isothermal flow, it becomes essential for more complex scenarios. For instance, turbulent flow, where fluid behavior is chaotic and unpredictable, requires more advanced equations and techniques due to the varying temperature and other conditions in the flow.
Examples & Analogies
Think of CFD like using a sophisticated weather model to predict storms. Just as meteorologists use complex algorithms to simulate atmospheric conditions, engineers employ CFD to model how fluids behave under various conditions, helping design better vehicles, buildings, and even medical devices.
Simplifying Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But in this course, we will try to simplify the equations to try to get analytical solutions for that. […] we will have a basic equation solver is the Euler equations.
Detailed Explanation
To make the Navier-Stokes equations manageable, we often simplify them to derive analytical solutions. One common approach is to look for specific conditions where viscosity effects are minimal, allowing us to use the Euler equations. By identifying these situations, engineers can derive simpler equations that describe the fluid behavior without the complexities of viscosity and turbulence.
Examples & Analogies
Imagine you are trying to solve a jigsaw puzzle, but some pieces are missing. You can only focus on the parts you have. In fluid mechanics, simplifying complex equations is like figuring out valid pieces to complete your picture. By assuming specific conditions (like neglecting viscosity), we can still gain valuable insights into fluid behavior.
Boundary Conditions in Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What are the boundary conditions we are imposing here on the bed of the sea? We can use the no flow boundary condition. […] the pressure or the waters, liquid is equal to waters and shear stress becomes a zero.
Detailed Explanation
Boundary conditions are critical in fluid dynamics as they define how fluids interact with their surroundings. For example, at the bed of a sea or river, we often impose 'no flow' boundary conditions, implying that fluid does not penetrate the surface. Additionally, we assume that pressure remains equal at the interface between two fluids like water and air, helping maintain an equilibrium that simplifies analysis.
Examples & Analogies
Think of boundary conditions as rules in a game. Just like players must follow certain rules to play fairly, fluid dynamics requires us to set conditions that fluids must comply with in order to accurately model their behavior, such as how they touch surfaces or interact with other fluids.
From Navier-Stokes to Euler and Bernoulli's Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you come to very basic things as we always look at interface between the air and waters that is many of the problems we solve it. […] those conditions where the viscosity does not dominate much.
Detailed Explanation
In many fluid problems, we transition from the more complex Navier-Stokes equations to the Euler equations, especially when viscosity is negligible. By assuming that viscous forces are minimal, we can derive Bernoulli's equations, which describe the conservation of energy along a streamline. This simplification allows for easier solutions while still providing useful insights into fluid behavior.
Examples & Analogies
Imagine you're swimming in a pool. When you swim slowly (like negligible viscosity), you glide smoothly across the surface, akin to Euler's equations. But during a chaotic splash fight with friends (where viscosity matters), the rules change completely. Similarly, understanding when to switch between complex and simple fluid behavior dynamics is essential in engineering and physics.
Assumptions in Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But try to understand it, the fluids are as nerdy as we, so it does not follow these conditions what we define it.
Detailed Explanation
When using Bernoulli's equation, certain assumptions are made: that the fluid is incompressible, steady, and flows along streamlines without viscosity effects. However, fluids can behave unpredictably and may not always meet these criteria. Engineers and scientists must recognize the limitations of these assumptions and apply them appropriately to get reliable results.
Examples & Analogies
Consider a road trip where you expect to travel steadily at 60 mph (the assumptions of Bernoulli). If you hit traffic (real-world complexities), your speed fluctuates. Understanding that the road conditions can change helps you better plan your trip, just as fluid engineers must consider real-world variability when applying Bernoulli's equation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Navier-Stokes Equations: A fundamental set of equations describing fluid motion.
-
Continuity Equation: Represents mass conservation in fluids, ensuring that mass input equals output.
-
Euler Equations: Simplified version of Navier-Stokes equations applicable under specific conditions.
-
CFD: A numerical method for analyzing fluid flows using computers.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing blood flow in arteries using Navier-Stokes equations to understand blockages.
-
Designing a tidal energy harvester that utilizes CFD to optimize turbine placement.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If fluids don’t compress, they flow with finesse, Navier and Stokes keep the motion blessed.
📖 Fascinating Stories
-
Imagine a racecar zooming; its smooth, sleek design represents low viscosity, while a thick molasses car illustrates high viscosity, stressing how each affects performance during the race.
🧠 Other Memory Gems
-
Remember 'MFVE' for Fluid Dynamics: M for Mass conservation, F for Forces (momentum), V for Viscosity, and E for Energy.
🎯 Super Acronyms
Use 'BIST' for Boundary Conditions
- B: for Boundary layer
- I: for Interface conditions
- S: for Shear stress balance
- T: for Tangential fluid velocity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of equations that describe the motion of fluid substances.
-
Term: Continuity Equation
Definition:
An equation that represents mass conservation in fluid dynamics.
-
Term: Euler Equations
Definition:
Equations that describe the flow of inviscid fluids, obtained from Navier-Stokes equations under specific conditions.
-
Term: Computational Fluid Dynamics (CFD)
Definition:
Numerical methods used to analyze fluid flows, providing approximate solutions to complex problems.
-
Term: Boundary Conditions
Definition:
Constraints applied at the borders of a fluid domain that affect flow characteristics.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to deformation or flow.
-
Term: Incompressible Fluid
Definition:
A fluid whose density does not change significantly with pressure.