Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to No Slip Boundary Condition
Unlock Audio Lesson
Good morning, everyone! Today, we're diving into a very important concept in fluid mechanics: the no-slip boundary condition. Can anyone tell me what this condition means?
I believe it means that the fluid velocity is zero at the boundary?
That's partially correct! The no-slip boundary condition states that the fluid's velocity is equal to the surface's velocity it’s in contact with. If the surface is stationary, then yes, the fluid velocity is zero there. This is crucial in preventing slip at the boundary.
So if the plate is moving, the fluid will move with it too?
Exactly! This adherence creates what we call a 'boundary layer,' where the velocity gradient exists. Remember: No slip = No sliding!
Effects of No Slip Condition on Fluid Flow
Unlock Audio Lesson
Now that we understand what the no-slip condition is, let’s discuss its effects. Why might this condition be important when analyzing fluid flow, like water flowing over a submerged plate?
It affects how the velocity changes near the surface?
Correct! The no-slip condition creates a boundary layer where the velocity gradually increases from zero at the wall to the maximum velocity away from it. If we're calculating drag forces on the plate, understanding this condition becomes vital.
What happens if the fluid isn't Newtonian?
Good question! The no-slip condition still applies, but the velocity profile and shear stress distribution might differ significantly with non-Newtonian fluids.
Applications of the No Slip Condition
Unlock Audio Lesson
Let’s look at some applications. In engineering, why is it significant to properly apply the no-slip boundary condition?
It helps in designing systems like pipes or ventilation systems, right?
Absolutely! For example, in designing pipelines, engineers must consider how fluid behaves at the boundaries to minimize losses and optimize flow. What about biological systems, like blood flow?
I imagine the no-slip condition would be crucial there too, since blood is flowing through arteries!
Exactly! Understanding how blood adheres to artery walls helps predict flow dynamics and potential blockages. Remember, the principles of fluid dynamics apply broadly!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the significance of the no-slip boundary condition in fluid mechanics, including how it affects fluid flow near solid surfaces. The concept is illustrated with examples such as flow past a stationary plate and interfaces between different fluids, emphasizing the need for equal velocities and shear stresses at boundaries.
Detailed
Detailed Summary
The no-slip boundary condition is central to understanding fluid dynamics, particularly in the context of the Navier-Stokes equations. This principle states that at a solid boundary, the fluid's velocity is equal to the boundary's velocity. This means if a fluid is flowing along a plate, the fluid particles in direct contact with the plate will not slip and thus have the same velocity as the plate itself, typically taken as zero if the plate is stationary. This condition helps define boundary layers and contributes to the overall analysis of viscous flows.
For example, in the flow of water over a surface, the water molecules adhere to the surface due to viscous effects, establishing a velocity gradient. This behavior significantly influences the pressure distribution and flow patterns. The section further examines how different fluids at an interface, such as water and air, must also adhere to the no-slip condition, leading to equal velocities and shear stress at the interface. Understanding these conditions is crucial for predicting flow behaviors in various engineering applications, such as the design of hydraulic systems and understanding biological flows, like blood in arteries.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the No Slip Boundary Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
No slip boundary condition is a fundamental principle in fluid mechanics that states when a fluid flows over a surface, the fluid in immediate contact with that surface has a velocity of zero relative to the surface. Therefore, if a fluid is moving with a velocity V, the fluid particles attached to a stationary surface also have to be moving at the same velocity, V_f = 0 along that surface.
Detailed Explanation
The no slip boundary condition is crucial because it defines how fluid interacts with surfaces. For instance, if water flows over a smooth metal surface, the water layer that is directly in contact with the metal does not slide over it; instead, it sticks to the surface. This means that the closest layer of fluid has no relative motion with respect to the surface, resulting in a transition from this layer to layers of fluid that may be moving more quickly.
Examples & Analogies
Think of this in terms of a person sliding down a slide. At the very starting point where they touch the slide, they don’t move (like the fluid particles sticking to the slide) until the entire system starts moving downwards. Just as the bottom layer of fluid doesn’t slip when it comes into contact with a surface, you also don't begin sliding down the slide until there is enough incline and a push to start moving.
Illustration of the No Slip Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
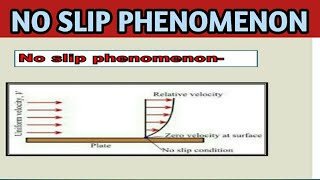
Consider a flat plate placed in a uniform flow of fluid. The fluid particles nearest to the plate will have very low velocity, reaching zero at the plate's surface. Beyond the boundary layer, the flow is affected minimally by viscosity, and the speed increases, resembling the velocity of the incoming flow.
Detailed Explanation
This chunk explains how fluid velocity profiles develop near a surface due to the no slip condition. When fluid flows over a stationary surface, a 'boundary layer' forms where the velocity gradually changes from zero at the surface (where the no slip condition is enforced) to the velocity of the incoming fluid at some distance away from the surface. This characteristic shapes how we analyze fluid flow in engineering applications, such as in pipes or around airplane wings.
Examples & Analogies
Imagine pouring syrup over pancakes. The syrup first contacts the pancake, where it is slow (zero velocity at the surface), and then as you pour more syrup, the layers of syrup on top begin to flow faster. This showcases how the no slip condition affects fluid movement and creates a gradient of speeds within the syrup.
Consequences of the No Slip Boundary Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As a result of the no slip boundary condition, boundary layers form, where velocities transition from zero (at the wall) to the free stream velocity. This transition impacts various flow characteristics, including shear stress and pressure distribution.
Detailed Explanation
The existence of these boundary layers due to the no slip condition leads to important consequences in flow dynamics. The varying velocities within the boundary layer cause the fluid to exert shear stress on the wall, which is a critical consideration in the design of pipelines, aircraft, and other systems. Understanding how shear stress varies can help engineers create more efficient designs.
Examples & Analogies
Think about how you feel when air flows over your skin while riding a bike. The air in contact with your skin is stationary relative to you, while the rest of the air moves past you more swiftly. This creates varying effects, like feeling cooler at high speeds and experiencing resistance. Like this air flow, fluids in pipes and over surfaces also create similar interactions dictated by shear stress and the no slip condition.
Interface Boundary Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When two fluids interact (e.g., air and water), the no slip condition still applies. The velocities at the interface must be equal, meaning the speed of the water must equal the speed of the air at their boundary.
Detailed Explanation
This describes how the no slip condition not only applies to solid surfaces but also governs interactions between fluids, showcasing the need for equilibrium between contacting fluid layers. The shear stress at the interface must also be the same, which influences how both fluids behave together.
Examples & Analogies
Imagine ice melting in water. The water molecules touching the ice have zero velocity relative to the ice, while the rest of the water flows past more quickly. This no-slip situation ensures that there is no mixing at the boundaries, affecting how the ice melts compared to the flowing water surrounding it.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
No Slip Condition: The principle that the fluid's velocity equals the surface's velocity it contacts.
-
Boundary Layer: The thin region where velocity transitions from zero to the free stream velocity.
-
Viscosity: The physical property that affects a fluid's flow behavior, especially at boundaries.
-
Newtonian Fluid: Fluids that exhibit a constant viscosity regardless of applied stress.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water flowing past a stationary plate, illustrating the no-slip condition.
-
Blood flow in arteries where red blood cells adhere to vessel walls due to viscosity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
No slip at the boundary line, fluid sticks and flows just fine.
📖 Fascinating Stories
-
Imagine a river flowing past a stationary rock; the water directly next to the rock stands still, just as a child standing next to a wall isn't moving either. This is the no-slip condition in action!
🧠 Other Memory Gems
-
SLEEK: Surfaces Lead to Equal velocities, Keep in mind!
🎯 Super Acronyms
NSBC
- No Slip Boundary Condition
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: No Slip Boundary Condition
Definition:
A fundamental principle stating that the velocity of fluid in contact with a solid boundary equals the velocity of the boundary.
-
Term: Boundary Layer
Definition:
A thin region adjacent to the boundary where the fluid velocity transitions from zero (at the boundary) to the free stream velocity.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to flow, affecting how the fluid interacts with boundaries.
-
Term: Newtonian Fluid
Definition:
A fluid whose viscosity remains constant regardless of the stress applied to it.