Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Navier-Stokes Equations
Unlock Audio Lesson
Good morning everyone! Today we are going to build on what we've learned about the Navier-Stokes equations. Can someone tell me what the Navier-Stokes equations represent in fluid mechanics?
They describe the motion of fluid substances!
Exactly! They consist of mass conservation and momentum equations. Now, these equations can be quite complex due to their nonlinear nature. Do you remember what our assumptions were regarding fluid properties?
We assume constant density for incompressible flow?
Yes! We also assume isothermal conditions and Newtonian fluid behavior. Who can summarize why these assumptions are important?
They help simplify the equations so we can derive solutions like Bernoulli's equations!
Great job! Let’s remember this with the acronym 'CIN' for Constant density, Isothermal conditions, and Newtonian fluid. Moving forward, we’ll derive Bernoulli's equations from these principles.
Deriving Bernoulli's From Euler Equations
Unlock Audio Lesson
Now, let’s talk about how we simplify the Navier-Stokes equations into the Euler equations and ultimately to Bernoulli's equations. Could anyone explain what Euler equations represent?
They describe the flow of an inviscid fluid, right?
Correct! Euler equations apply when viscosity is negligible. As we derive Bernoulli's equations, we’ll focus on flow along streamlines. Can anyone remember what that entails?
It involves looking at the flow characteristics in paths that fluids take without crossing, right?
Yes! Along these paths, we find that inertial and pressure forces balance out. This allows us to equate energy terms without considering viscous forces. Let’s keep this idea in mind as we proceed.
Assumptions Behind Bernoulli’s Equations
Unlock Audio Lesson
When using Bernoulli's equations, we have various assumptions. Can someone list some of these assumptions?
We consider the flow to be steady, frictionless, and incompressible.
Perfect! And do you understand why those assumptions are critical?
Because they allow for the conservation of energy between different flow points!
Exactly right! It’s playing off energy conservation principles. Now let’s apply this understanding with a practical example of fluid flow in a pipe.
Applications of Bernoulli's Equations
Unlock Audio Lesson
Can anyone think of practical scenarios where Bernoulli's equations are applied?
Airplanes use it to understand lift!
Exactly! And we also see it in pipe flow and blood flow in arteries due to blockages. How do you think Bernoulli's principles help us understand these situations?
They help us predict how pressure will change in those scenarios and manage flow more efficiently!
Great answer! It’s all about forecasting and controlling various fluid behaviors in applied mechanics.
Review of Bernoulli's Applications
Unlock Audio Lesson
Before we wrap up, let’s quickly summarize what we’ve learned about Bernoulli's equations. Who can share the key points?
We derived them from Navier-Stokes equations using assumptions like steady flow, no viscosity, and fluid incompressibility.
And they help explain how energy conservation applies for flowing fluids in various real-world examples!
Perfect summaries! Always remember this relationship as it’s a cornerstone of fluid dynamics. Practice with examples in everyday life to strengthen your understanding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section provides an in-depth exploration of how Bernoulli's equations can be derived from the Navier-Stokes equations through a series of assumptions relevant to fluid dynamics, especially for incompressible, Newtonian fluids. Key concepts such as inertia, pressure, and viscous forces are discussed in the context of fluid flow mechanics.
Detailed
Detailed Summary
In this section, we delve into the derivation of Bernoulli's equations from the Navier-Stokes equations, fundamental in fluid mechanics. The process begins with the four Navier-Stokes equations, addressing mass conservation and linear momentum for incompressible Newtonian fluids. The assumptions crucial for these derivations include:
- Constant Density: This indicates incompressible flow where density does not vary significantly.
- Isothermal Conditions: A constant viscosity is assumed, indicating no large temperature fluctuations.
- Newtonian Fluid Behavior: The fluid's viscosity remains constant, allowing for linear relationships between shear stress and velocity gradient.
The discussion highlights how simplifications, such as neglecting viscosity or considering flow along streamlines, lead to the well-known Bernoulli's equations—demonstrating the relationship between velocity, pressure, and elevation in a fluid flow system. This derivation notes sequential simplifications from the more complicated Navier-Stokes framework and provides practical illustrations like flow in arteries or river systems, enhancing comprehension of fluid dynamics principles.
Youtube Videos
![Deriving Bernoulli's Equation in 1 Video [Physics of Fluid Mechanics #53]](https://img.youtube.com/vi/KuuLwRt6LQ4/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Deriving Bernoulli's Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
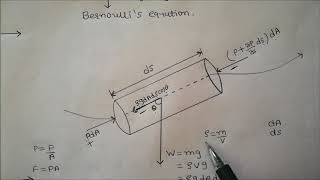
Today, we will talk about how we can derive these Euler equations along the streamlines that we can derive as a Bernoulli's equation.
Detailed Explanation
In this part, we are introducing the concept of deriving Bernoulli's equations from the Euler equations. This implies we're looking at fluid flow along streamlines, a path that fluid particles follow. Understanding this flow helps us set up the equations effectively because streamlines assume that the velocity of fluid is constant along its path.
Examples & Analogies
Imagine water flowing gently in a straight river. The imaginary lines that represent the paths taken by the flowing water are like streamlines. Just as a swimmer tries to take the easiest path through the water, fluid particles also follow these path lines which help us understand their movement.
Assumptions for Derivation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Whenever you apply the Bernoulli's equations... along the streamlines. Those things we will discuss more, but please remember it all the things are derived from very basic equations is the Navier-Stokes equations.
Detailed Explanation
Here, we introduce the assumptions needed to derive Bernoulli's equations. Essential conditions for using the equations include that fluid flow must be steady, incompressible, and frictionless. These assumptions simplify the complex flow of fluids into manageable equations by focusing on certain conditions under which these equations hold true.
Examples & Analogies
Think of a slide at a water park. When you slide down smoothly without any bumps (frictionless) and maintain a constant speed when starting from the top (steady), you can predict how quickly you'll reach the bottom. The same principles apply to fluids, making it easier to calculate things like pressure change.
Understanding Euler's Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the basic equations is the Euler equations which for frictional less or less viscosity...
Detailed Explanation
Euler's equations are fundamental in fluid dynamics, particularly for ideal fluids with negligible viscosity. They capture the essential physics of fluid motion. When we derive Bernoulli's equations, we rely on a simplification of these equations along a streamline to express energy conservation principles—this leads us to understand how pressure varies with velocity.
Examples & Analogies
Picture riding a bicycle downhill. Your speed increases as the hill gets steeper, and your braking (similar to pressure) decreases as your speed increases. This relationship between speed and pressure helps explain how the bike accelerates down the hill.
Integration along the Streamline
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If that components are 0, then I think you have very simple things to do the integrations... if I consider it, streamline and having points 1 and 2 this is the streamline S1.
Detailed Explanation
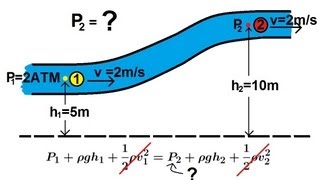
This section discusses the importance of integrating along the streamline when deriving Bernoulli's equations. The assumption that certain terms equal zero simplifies our calculations and makes the integration straightforward, allowing us to assess pressure differences between points in the fluid flow.
Examples & Analogies
Imagine you’re measuring the height of a water fountain. If you take measurements only at two heights (points 1 and 2) along the stream of the fountain, you can see how the height of the water decreases as it moves outward. In the same way, integrating along the streamline allows us to see how pressure changes at different points.
Final Assumptions and Conclusion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, not to use the Bernoulli sequence just like that... that the reason we use the Bernoulli's equation, many of the places where these assumptions are not valid.
Detailed Explanation
The conclusion emphasizes understanding the limitations of Bernoulli's equations and the assumptions underlying their use. While they provide valuable insights into fluid dynamics, these assumptions may not hold true in every situation. Recognizing this will help us apply Bernoulli's equations judiciously.
Examples & Analogies
Consider a person trying to run through a crowded room. While they can move quickly in open spaces (like ideal fluid flow), they face obstacles (like viscosity) when navigating through people. Understanding where you can move smoothly versus where you need to slow down reflects the realities of fluid flow in various contexts.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Navier-Stokes Equations: Fundamental equations governing fluid motion incorporating mass and momentum.
-
Bernoulli's Principle: A principle stating that where fluid velocity is high, pressure is low, and vice versa.
-
Incompressible Flow: Fluid flow where density remains unchanged, simplifying calculations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The flight of an airplane is influenced by Bernoulli's principle, where air moves faster over the wing, resulting in lower pressure and lift.
-
Blood flow in arteries demonstrates Bernoulli's equations, particularly during blockages, altering pressure and flow rates.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the flow, pressure drops low, speed gains a show; Bernoulli's way, in arcs they sway.
📖 Fascinating Stories
-
Once upon a time in a peaceful village, the wind flowed over the hills. As it sped up, it would lower the pressure, lifting the leaves high; a magical demonstration of Bernoulli's principle.
🧠 Other Memory Gems
-
Remember 'PVE' for Bernoulli's - Pressure, Velocity, Elevation.
🎯 Super Acronyms
CIN for assumptions
- Constant density
- Isothermal conditions
- Newtonian fluid.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Incompressible Flow
Definition:
A flow condition under which the density of a fluid remains constant.
-
Term: Newtonian Fluid
Definition:
A fluid whose viscosity remains constant regardless of the stress applied to it.
-
Term: Viscous Forces
Definition:
Forces that resist the flow of fluid due to its viscosity.
-
Term: Steady Flow
Definition:
Fluid flow where the velocity at a point does not change with time.
-
Term: Bernoulli's Equation
Definition:
An equation expressing the principle of conservation of mechanical energy in fluid flow.