Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Navier-Stokes Equations
Unlock Audio Lesson
Welcome class! Today, we are discussing the Navier-Stokes equations, which govern the motion of fluid substances. Can anyone tell me what variables these equations depend on?
They depend on velocity, pressure, and density, right?
Exactly! The equations involve the velocity field and pressure for incompressible fluids. Remember, we often denote the velocity components as 'u', 'v', and 'w' for the x, y, and z directions, respectively.
What assumptions do we make when using these equations?
Great question! We assume incompressible flow, constant viscosity, and, in many cases, isothermal conditions. These assumptions simplify our calculations significantly.
How do we use these equations practically?
We use them to solve complex problems in fluid dynamics, but we often apply approximations to obtain more manageable forms, such as the Euler equations.
To remember these assumptions, we can use the acronym 'CIN': Constant viscosity, Isothermal conditions, No compressibility. Let's summarize: what are the four key components we identify with Navier-Stokes?
Velocity, Pressure, Density, and Assumptions!
Deriving Euler Equations
Unlock Audio Lesson
Moving on, let's talk about when to apply Euler equations. Can someone explain when we use them instead of Navier-Stokes?
We use Euler equations when viscosity is negligible, right?
Yes! That leads to a simplification of Navier-Stokes equations. So, can anyone explain what Euler's equations look like?
They describe mass conservation and acceleration without accounting for viscous forces.
Exactly! Now, consider how we represent force balance in these equations—what forces are at play?
Only pressure and gravity, when viscosity is not a factor.
Correct! Remember, this simplification opens paths to derive Bernoulli's equation by integrating along streamlines. Can anyone recall the conditions where Bernoulli's equation applies?
Steady flow along streamlines without friction!
Right again! Let’s summarize: Euler equations stem from Navier-Stokes under which conditions?
Negligible viscosity and constant temperature!
Bernoulli's Equation
Unlock Audio Lesson
Now, let’s derive Bernoulli’s equation from Euler equations. How do we do this?
By integrating Euler’s equations along streamlines, right?
Exactly! And what concepts do we assume while deriving Bernoulli's equation?
We assume incompressible flow, no viscosity, and steady flow.
Remember, these are critical assumptions! Now, can anyone explain what Bernoulli’s equation represents?
It represents the conservation of energy in fluid flow, combining pressure energy, kinetic energy, and potential energy.
Very well put! So, why should we be cautious when applying Bernoulli's equation in real scenarios?
Because they might not hold in turbulent or compressible flows!
Exactly! So, concisely, Bernoulli's equation assumes what three components of energy conservation?
Pressure, Kinetic, and Potential Energy!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the Euler equations, which describe the motion of fluid particles under the influence of pressure and gravity without viscosity. It follows the simplification of the Navier-Stokes equations under specific assumptions to derive Bernoulli's equations, which are fundamental in understanding fluid dynamics in practical applications.
Detailed
Euler Equations and Bernoulli's Equations
This section discusses two fundamental equations in fluid mechanics: the Euler equations and Bernoulli's equations. It begins with a recap of the Navier-Stokes equations, which describe the motion of incompressible Newtonian fluids. We can simplify these equations under specific conditions, such as assuming constant viscosity and negligible viscosity effects, leading us to Euler's equations that characterize ideal fluid flow.
Key Concepts:
- Navier-Stokes Equations: Describe continuity and momentum conservation for fluid flow.
- Euler Equations: Simplified equations derived from Navier-Stokes when viscosity is negligible, focusing solely on accelerative forces like pressure and gravity.
- Bernoulli's Equations: These arise from applying Euler's equations along streamlines and illustrate the principle of conservation of energy in fluid flow.
Significance:
Understanding these fundamental equations and their derivation allows engineers and scientists to model fluid behavior in various applications, from aerodynamics to hydraulics, leveraging approximations and assumptions to simplify complex scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Euler Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As I was discussing, if it is a condition where these terms are 0 in a particular fluid flow, if these terms = 0 then these equations become a very linear form of very simplified equations that is what we call the Euler equations. That means we have ρ (dV/dt) = ρg + (∇ • Φ).
Detailed Explanation
Euler equations are derived from the Navier-Stokes equations under the assumption that viscosity plays a negligible role in the flow, meaning the influences from viscous forces are minimal. In this context, the term for viscous stress vanishes, simplifying the equations to their Euler form, where the only forces acting are gravity and pressure forces. This simplification allows fluid flow to be analyzed without considering the complexities introduced by viscosity.
Examples & Analogies
Consider water flowing through a large pipe at a constant speed. If the flow is steady and the viscosity of the water is minimal (like in a smooth pipe), we can assume that the flow adheres closely to the Euler equations without the need to account for the slowing effects of viscosity. Think of it as a car cruising on a smooth highway at a constant speed without friction slowing it down.
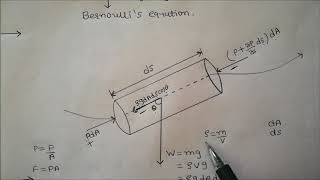
Derivation of Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
from these Euler equations, we can derive very basic equations as you know it is the Bernoulli's equations. As we discussed in previous classes, we do a series of assumptions and based on that series of assumptions, we apply the linear momentum equations along a streamline. That is the Bernoulli's equations.
Detailed Explanation
Bernoulli's equation is derived from the Euler equations by applying the principle of conservation of energy along a streamline under specific assumptions: steady flow, incompressibility, and no friction losses. This results in an equation relating pressure, velocity, and height in a fluid system. Essentially, as fluid moves through different areas in a streamline, changes in speed and elevation result in changes in pressure, ultimately leading to the relationship described by Bernoulli's principle.
Examples & Analogies
Imagine water flowing through a garden hose. When you partially block the end of the hose, the water speeds up as it exits, leading to decreased pressure at the narrowest point. This is the Bernoulli effect in action. The speeding water means that there is less pressure at that point compared to where the hose is wider, illustrating the relationship between speed and pressure in fluid dynamics.
Assumptions in Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Many times, you apply the Bernoulli's equations also you do not know the assumptions behind that. Please remember it all the things are derived from very basic equations which are the Navier-Stokes equations.
Detailed Explanation
The application of Bernoulli's equation is dependent on several assumptions which must be fulfilled for the equation to hold true. This includes steady, incompressible flow and negligible viscosity, meaning that real-world conditions can often lead to misunderstandings or misuse of Bernoulli's equation when these conditions are not valid. Understanding these assumptions helps ensure that the equation is applied correctly.
Examples & Analogies
Think about riding a bike downhill; if you're going too fast and the road is rough, you may experience bumps that disrupt your smooth motion. Similarly, if in fluid mechanics the assumptions of Bernoulli's are not met, applying the equation can lead to 'bumpy' errors in predictions, just like hitting those bumps when riding your bike.
Challenges with Real-World Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fluids are not as good or as ideal. They're naughty; they don't follow these boundary conditions you talk about: steady, streamlines, they're frictionless.
Detailed Explanation
In practical scenarios, real fluids exhibit properties like turbulence and varying viscosity, making it difficult to strictly apply Bernoulli's principle. Understanding the limitations of these equations in complex fluid flows is crucial for effective predictions in engineering applications. Acknowledging that all fluids behave differently under varied conditions helps engineers refine their approaches and tools when dealing with fluid dynamics.
Examples & Analogies
Imagine trying to ride your bike on a windy day; the wind pushes you off course, making it harder to maintain a steady line—instead of a smooth ride downhill, you might find yourself swerving unexpectedly. This unpredictability mimics the way real fluids can behave differently than theoretical models suggest.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Navier-Stokes Equations: Describe continuity and momentum conservation for fluid flow.
-
Euler Equations: Simplified equations derived from Navier-Stokes when viscosity is negligible, focusing solely on accelerative forces like pressure and gravity.
-
Bernoulli's Equations: These arise from applying Euler's equations along streamlines and illustrate the principle of conservation of energy in fluid flow.
-
Significance:
-
Understanding these fundamental equations and their derivation allows engineers and scientists to model fluid behavior in various applications, from aerodynamics to hydraulics, leveraging approximations and assumptions to simplify complex scenarios.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In fluid flow around a wing, Bernoulli's equation explains how varying velocities lead to pressure differences, generating lift.
-
Water flow in a pipe narrows leading to increased velocity and reduced pressure, as described by Bernoulli's principle.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids high and low, pressure's flow, fast they go, energies to show!
📖 Fascinating Stories
-
Imagine a water slide; as water rushes down, it speeds up and creates lower pressure behind it, lifting you gently upward—a Bernoulli moment!
🧠 Other Memory Gems
-
Use 'PEEK' to remember: Pressure, Energy, Kinetic energy for Bernoulli.
🎯 Super Acronyms
KNIFE = Kinetic energy, Newton's laws, Incompressibility, Frictionless for fluid simplifications.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
Equations describing the motion of fluid substances based on the principles of momentum and mass conservation.
-
Term: Euler Equations
Definition:
Simplified equations derived from the Navier-Stokes equations, neglecting viscous forces in fluid motion.
-
Term: Bernoulli's Equations
Definition:
A principle describing the conservation of energy in a flowing fluid, relating pressure, velocity, and height.
-
Term: Incompressible Flow
Definition:
Flow where the fluid density remains constant.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to deformation or flow.