Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
No-slip Boundary Condition
Unlock Audio Lesson
Good morning class! Today, we will start by discussing the no-slip boundary condition. Can anyone explain what it means?
Isn't it where the fluid velocity at a solid surface is zero?
Exactly, Student_1! The fluid sticks to the solid boundary. This means the fluid particles at the boundary have the same velocity as the boundary itself. This is critical when analyzing fluid flow around objects.
What happens if the boundary is moving?
Great question, Student_2! If the boundary moves, then the velocity of the fluid at that interface matches the boundary velocity. Let's remember this concept with the mnemonic: 'No Slip, No Leap'. It means fluid does not leap forward at the boundary, keeping it close!
Could you give an example of when this is significant?
Certainly! Think about water flow past a stationary rock in a river. The water immediately next to the rock is at rest relative to it. This can affect the overall velocity profile downstream.
To summarize, the no-slip condition plays a vital role in fluid dynamics by influencing how fluid behaves at the interface of solid objects.
Interface Conditions Between Fluids
Unlock Audio Lesson
Now, let's move on to **interface conditions**. What happens at the boundary between two different fluids?
Their velocities must match at the boundary, right?
Correct, Student_4! Not only must their velocities match, but the shear stresses acting on both sides of the interface must also be equal.
Can you explain what shear stress is?
Shear stress relates to how one fluid 'drags' on another. Using Newton's law of viscosity, we can relate shear stress to the velocity gradient across the interface. Remember, 'Strong Bond, Equal Stress!' helps us visualize the balance at the interface.
How does this apply to real-world situations?
A fantastic question! It’s crucial in areas like blood flow in arteries. If there’s a blockage, the velocities and shear stresses at the interface between blood and artery walls change, impacting the flow.
To conclude, understanding interface conditions helps us predict fluid behavior when different fluids interact, particularly in complex systems.
Mathematical Representations
Unlock Audio Lesson
Let’s delve into the mathematics behind these conditions. How do we express the relationships between different fluids?
Using the laws of viscosity, right? We can relate shear stress to the velocity gradient?
Spot on, Student_3! We can express it as τ = μ (du/dy), where τ is shear stress, μ is dynamic viscosity, and du/dy is the velocity gradient. Remember, 'Viscosity Equals Response'.
Could you give us a practical situation where this matters?
Absolutely! In an industrial setup where oil flows through a pipe either bordered by air or water, applying the correct shear stresses at the boundary ensures efficient flow and prevents turbulence.
In summary, laying out the mathematical framework offers insight into both designing systems effectively and predicting how fluids will perform under various conditions.
Real-world Fluid Dynamics Applications
Unlock Audio Lesson
Now, let’s talk about real-world applications. Who can think of an example where boundary conditions are critical?
I think about blood flow in arteries with blockages!
Excellent, Student_1! In this case, the blockage alters both velocity profiles and pressure distributions. One of the important applications of fluid mechanics is predicting these changes.
What about other fields? Can we consider turbines or engines?
Absolutely! In tidal energy systems, understanding how water interacts with turbines involves analyzing the interface conditions to maximize energy extraction.
How can we relate this back to our Navier-Stokes studies?
Great connection, Student_4! The Navier-Stokes equations establish the foundation for simulating and analyzing fluid behavior, especially when understanding complex interactions at interfaces.
In closing, the knowledge of interface boundary conditions is essential in applying fluid mechanics principles across multiple domains.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the significance of interface boundary conditions in fluid mechanics. It elaborates on the concepts of no-slip condition and interface balance of velocities and shear stresses between different fluids, grounding these concepts within the framework of the Navier-Stokes equations.
Detailed
Interface Boundary Conditions
In fluid mechanics, understanding interface boundary conditions is crucial for analyzing the behavior of fluids within different flow domains. This section primarily focuses on the Navier-Stokes equations, which are fundamental in fluid dynamics and may be simplified under various assumptions.
Key Points Covered:
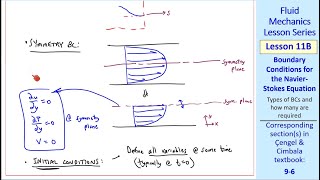
- No-slip Boundary Condition: This condition states that the fluid's velocity at the boundary of a solid object is equal to the velocity of that boundary itself. For instance, if a fluid flows past a stationary plate, the velocity of the fluid at the plate surface is essentially zero.
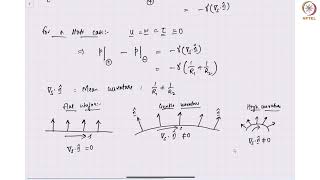
- Interface Conditions: When two different fluids are in contact, the interface boundary conditions dictate that the velocities of the two fluids must be equal at the interface. Furthermore, the shear stresses must also balance, establishing equilibrium across the interface.
- Mathematical Relations: The section details how the use of Newton's laws of viscosity aids in creating relationships between the velocities of different fluids at their interface, leading to critical insights into fluid behaviors.
- Application in Real Scenarios: Examples include analyzing blood flow through arteries as influenced by blockages, where flow patterns and pressure distributions change critically due to boundary conditions.
This framework sets the stage for understanding more complex fluid behaviors in subsequent lessons.
Youtube Videos
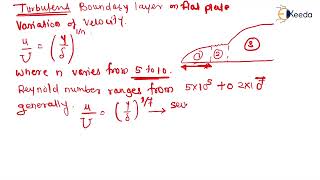
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let me go to very interesting part is that many of the times also we can write the same form for cylindrical coordinate systems. We are not going to discuss in this class, but please have a practice to write this mass conservation equations and r components. As you know it is a cylindrical coordinates we have a r theta and z. So, these equations are there. It looks complex equations, no doubt about that, but please has to look at these equations which also is the same form of what we discuss of, this is the same vectorial form of what we discuss for the Cartesian coordinate system.
Detailed Explanation
In understanding fluid mechanics, one must get familiar with how boundary conditions affect flow behavior, particularly at interfaces between different fluids. This section highlights the need to understand these conditions for both cylindrical and Cartesian coordinate systems, emphasizing their relevance in various applications, including engineering.
Examples & Analogies
Consider a river flowing into a lake (an interface). Understanding how the water will interact at that boundary helps in predicting sediment deposits and ecological impacts.
No Slip Boundary Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, let us go for a as I discussed that using the Navier-Stokes equations we can simplify it find out these basic derivations of the Bernoulli's equations from Euler equations that derivations part I am showing it how will this mathematics components are available in f m white book. So, please go through that I will be conceptually I will try to explaining you that how we can derive from Navier's equations to Euler equations. From Euler equations we can derive it what is the Bernoulli's equations that is the part we will discuss now.
Detailed Explanation
The no slip boundary condition is a fundamental concept in fluid mechanics that states that at the interface of a fluid and a solid, the fluid's velocity is equal to the solid's velocity. Essentially, if a fluid is in contact with a surface, it will not slide over that surface at the point of contact, but adhere to it instead. This leads to varied fluid velocities across different layers or boundaries.
Examples & Analogies
Think about putting your hand in a stream of water. At the point your hand touches the water, the water is stationary relative to your hand, demonstrating the no slip condition—there's no sliding, just adherence.
Interface Boundary Conditions Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
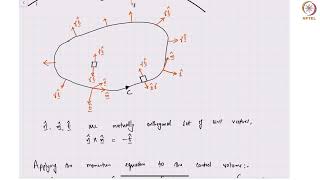
Now if you come to very basic things as we always look at interface between the air and waters that is many of the problems we solve it. So, in that case if I look at u water should be equal to u air that is ok. So that means at the interfaces levels I will get it the velocity of water is equal to velocity of air at the three surface levels. Also I will get it the shear stress working on waters that is what will be shear stress working on air that should be.
Detailed Explanation
At an interface between two different fluids, like air and water, the velocity of the fluids must match, according to the no slip boundary condition. This means that if you have a layer of air above water, the water at the surface is moving at the same speed as the air at that interface. Additionally, the shear stresses exerted by the fluids on each other must also be equal, enabling a stable transition between each fluid environment.
Examples & Analogies
Consider a swimming pool. As you swim, the water at the surface where it meets the air must move in sync with the air above it. If you dive in quickly, you can feel how the water acts upon your body, and that interaction is dictated by interface boundary conditions.
Implications of Different Fluid Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the problems as you know it, the dynamic viscosity of the water will be much larger as compared to the dynamic velocity of waters. For example, m waters as larger than 50 times of m waters. That is the reasons. So if somebody is 50 times or larger, then definitely this will be the smaller than the 50 times.
Detailed Explanation
Understanding the difference in properties between fluids, such as their viscosities (a measure of resistance to flow), is crucial for predicting fluid behavior at interfaces. Water typically has a high viscosity compared to gases like air, which means that at their interface, the water will exert more resistance to movement than air, leading to different flow behaviors and gradient profiles.
Examples & Analogies
Think about how hard it is to stir honey (which has high viscosity) compared to water. In mixed environments, like at the surface of a lake, water will flow freely while air moves more quickly, which affects overall flow patterns.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
No-slip Boundary Condition: The fluid velocity at a solid boundary is zero.
-
Interface Conditions: Must match velocities and shear stresses at the interface of two fluids.
-
Dynamic Viscosity: A measure of a fluid’s internal resistance to flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Blood flow in arteries, particularly at areas of blockage, demonstrating changes due to interface conditions.
-
Water flow past obstacles, showcasing the no-slip condition where fluid velocity at the obstacle surface is zero.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Fluid's velocity stays on track, at the boundary, it’s like a pact.
📖 Fascinating Stories
-
Imagine a slow river flowing past a rock, where the water hugs the rock closely, never racing ahead, illustrating the no-slip concept.
🧠 Other Memory Gems
-
V.E.S. - Velocity equals Shear at the interface; remember this at all times!
🎯 Super Acronyms
N.S.B.C. - No Slip Boundary Condition.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Noslip boundary condition
Definition:
The condition where the velocity of a fluid at the boundary of a solid is equal to the velocity of the solid surface.
-
Term: Interface conditions
Definition:
Conditions at the boundary between two different fluids where velocities and shear stresses must be equal.
-
Term: Shear stress
Definition:
The stress that acts parallel to the surface area of a material, impacting its deformation or flow.
-
Term: Dynamic viscosity (μ)
Definition:
A measure of a fluid's resistance to flow; it quantifies internal friction.