Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Navier-Stokes Equations
Unlock Audio Lesson
Today, we will start by revisiting the Navier-Stokes equations. Can anyone tell me the significance of these equations in fluid mechanics?
They describe how fluids behave under the influence of various forces?
Exactly! The Navier-Stokes equations account for mass conservation, momentum, and the effects of viscosity. Now, what happens when we assume certain conditions? What are some simplifications we often make in fluid flow?
We may assume that flow is incompressible and that viscosity is negligible for certain conditions.
Correct! These assumptions lead us to the Euler equations, which we will explore next. Remember, 'ICE' - Incompressibility, Constant viscosity, and Equilibrium conditions. It helps to remember the types of fluids we are dealing with. Let’s move on to those conditions in detail.
Conditions for Simplification
Unlock Audio Lesson
Now let's discuss the specific conditions necessary for applying the Euler equations. Who can recall the definition of incompressibility?
Incompressibility means that the fluid's density doesn't change regardless of pressure changes.
Great! Incompressibility is vital for simplifying the mass conservation equations. What about the assumptions of Newtonian fluids?
Newtonian fluids have a constant viscosity regardless of the flow conditions.
Exactly! By assuming constant viscosity, the behavior of the fluid can be more predictable. Remember the acronym 'IVC' for Incompressibility, Viscosity constant, and the conditions that simplify flow. Let’s relate these to some real-world applications.
Boundary Conditions in Fluid Flow
Unlock Audio Lesson
Next, we will review boundary conditions in fluid flow. Can someone explain what a no-slip boundary condition means?
The no-slip condition means that the fluid at the boundary has the same velocity as that of the boundary surface.
Exactly! This condition plays a critical role in understanding viscous flow. Now, can someone give me an example of where interface boundary conditions might be applied?
An example would be between air and water, like at the surface of a lake.
Yes! And understanding these boundaries helps us define how fluids interact with surfaces. Remember, 'NISI' - No-slip, Interface, Stability, and Interactions. Let’s wrap up this session.
Applications of Euler Equations
Unlock Audio Lesson
Let’s explore practical applications of the Euler equations. Can anyone provide an example that illustrates the use of Euler equations in an engineering context?
Blood flow through arteries, as the viscosity is often ignored for larger vessels.
Exactly! In larger arteries where inertial forces dominate, Euler equations simplify analysis significantly. Can anyone think of another field where these principles might apply?
In civil engineering, for example, analyzing water flow under a bridge.
Great example! Understanding how streamlines are affected will allow us to apply the equations more effectively. Always remember to assess which assumptions are applicable in each scenario. Let's summarize what we've covered.
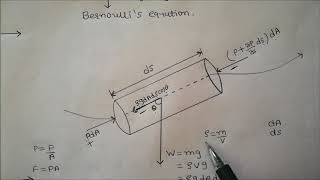
Linking to Bernoulli's Equation
Unlock Audio Lesson
Finally, let’s discuss how we can derive Bernoulli's equation from Euler's equations. What are the conditions for using Bernoulli's equation?
Bernoulli's equation is applied along streamlines for steady, incompressible, and non-viscous flows.
Right! So if we have Euler’s equations in steady flow, we can use Bernoulli using those same assumptions. Remember: 'SCIV' - Steady flow, Compressibility, Incompressibility and Viscosity assumptions! Now can anyone summarize how all concepts relate?
We simplify from complex Navier-Stokes to Euler equations and finally to Bernoulli’s, based on these practical conditions.
Perfect! You've summarized the essence of connectivity among these concepts in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the key assumptions and conditions that lead to the Euler equations being a simplification of the Navier-Stokes equations for inviscid, incompressible flows. Fundamental concepts such as mass conservation, momentum equations, and the application of boundary conditions in fluid mechanics, particularly focusing on various fluid flow scenarios, are presented.
Detailed
Detailed Summary
In this section, we delve into the simplifications of the Navier-Stokes equations under specific conditions that allow for the formulation of the Euler equations, applicable to incompressible flows. The key assumptions include: 1. Incompressibility: Fluid density remains constant. 2. Newtonian fluids: Viscosity is constant. 3. Isothermal conditions: Temperature remains stable. 4. Steady flow: Assumes no fluctuation of flow characteristics over time.
The chapter also emphasizes the importance of boundary conditions, such as no-slip conditions and interface boundaries. Moreover, we went through examples illustrating how these simplifications manifest in various practical scenarios, such as blood flow in arteries and water flow around obstacles. Understanding these conditions is vital for transitioning from the complex forms of the Navier-Stokes equations to the more manageable Euler equations. Finally, this understanding sets the stage for deriving Bernoulli's equation from the Euler equations, emphasizing the essential role of simplifications in fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Assumptions for Simplifying Fluid Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the context of deriving fluid equations, we consider certain assumptions which are crucial for forms like the Euler equations. These include:
1. Incompressible Flow where density remains constant.
2. Newtonian Fluid where viscosity is constant.
3. Isothermal Conditions where temperature does not vary significantly.
These assumptions allow simplifications to governing equations.
Detailed Explanation
In fluid mechanics, certain assumptions simplify complex equations. When fluid flow is marked as incompressible, we assume its density does not change. This means the mass per unit volume stays constant. Additionally, by defining a fluid as Newtonian, we recognize that its viscosity (a measure of its resistance to deformation) remains consistent across various conditions. Isothermal conditions indicate temperature stability within the fluid. Together, these assumptions streamline the equations governing fluid motion.
Examples & Analogies
Consider a rubber ball that stays the same shape and size when you push it; it's an incompressible fluid. Now imagine honey—this is a Newtonian fluid because it flows predictably under pressure. Lastly, think of water boiling in a pot where the temperature is constant; that symbolizes isothermal conditions. All these real-life examples help illustrate the concepts behind simplifying fluid equations.
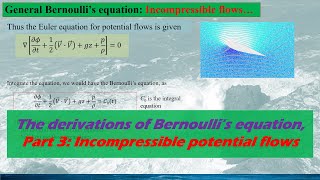
Transition from Navier-Stokes to Euler Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Euler equations arise from the Navier-Stokes equations when the viscous forces are negligible. When viscosity approaches zero, the equations simplify significantly. In this situation, the equations reduce essentially to expressions balancing acceleration with forces from gravity and pressure.
Detailed Explanation
The Navier-Stokes equations describe how fluids flow, incorporating the complexities of viscosity. However, under certain conditions—like when viscosity is minimal or negligible—the equations transform into the Euler equations. This shift simplifies the calculations, removing viscous terms, allowing us to focus on the forces acting on the fluid, such as gravity and pressure changes. Essentially, this means fluid behavior can often be approximated without considering frictional effects.
Examples & Analogies
Imagine a smooth slide at a playground; when you go down, the lack of friction lets you slide quickly. This is like a fluid flow where we neglect viscosity. In contrast, think about moving through molasses, where the stickiness (or viscosity) slows you down significantly—a situation where the Navier-Stokes equations are relevant.
Understanding Non-linear Terms in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Within the context of the Euler equations, the term for convective acceleration includes non-linear components. Understanding these non-linear terms is crucial as they affect the flow characterization, particularly in turbulent situations.
Detailed Explanation
In fluid dynamics, terms in equations can be classified as linear or non-linear. Non-linear terms often arise from products of velocity components and their gradients. These terms complicate our ability to derive analytical solutions. For instance, in turbulent flow (where chaotic changes happen), the presence of these non-linear terms makes predictions much more complex. Understanding and managing these terms is vital in the study of fluid flow behavior.
Examples & Analogies
Think of a chaotic dance floor where a group of people moves randomly. Each person's movement affects others nearby, leading to unpredictable patterns. This scenario aligns with how non-linear terms interact within fluid flow—each tiny change can dramatically influence the overall behavior of the flow, just as one dancer's move can affect many around them.
Equations of Motion in Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Euler equations incorporate the local acceleration, which links the change in velocity over time, with gravitational and pressure forces contributing to the flow. This interconnectedness illustrates the primary balance of forces at play within the fluid.
Detailed Explanation
Understanding the Euler equations involves recognizing the local acceleration's role, representing how quickly the fluid's velocity changes over time. This local acceleration is influenced by external forces, including gravity and pressure differences within the fluid. When these forces are balanced correctly, they describe the fluid motions accurately. Each component connects back to the basic principles of momentum and fluid motion.
Examples & Analogies
Picture a rollercoaster at the top of a hill. As gravity pulls it down, the speed increases—increasing local acceleration. The smoother the ride, the more balanced these forces are. Similarly, the Euler equations capture this balance of forces in fluid dynamics, ensuring an accurate forecast of fluid behavior.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Incompressibility: The fluid’s density does not change, crucial for simplification to Euler equations.
-
No-Slip Condition: The velocity at a boundary matches that of the boundary itself, significant for viscous fluid interactions.
-
Euler Equations: They describe motion under the assumption that viscous forces are negligible.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Blood flow in large arteries where viscous effects are minimal.
-
Water flow around objects in civil engineering, simplifying the Navier-Stokes equations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In flow where viscosity is slight, the Euler gives us insight!
📖 Fascinating Stories
-
Imagine a river where the water flows smoothly over the rocks. The water sticks to the rocks due to the no-slip condition, and the flow remains the same depth, illustrating incompressibility.
🧠 Other Memory Gems
-
Remember SICE for assumptions: Steady flow, Incompressibility, Constant viscosity, Equilibrium conditions.
🎯 Super Acronyms
NICE
- No-slip
- Interface
- Constant viscosity
- Equilibrium for recalling flow conditions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of equations that describe the motion of fluid substances based on principles of conservation of mass, momentum, and energy.
-
Term: Euler Equations
Definition:
Simplified equations derived from the Navier-Stokes equations that apply to inviscid flows, where viscous forces can be neglected.
-
Term: Incompressibility
Definition:
Assumption indicating that the fluid density remains constant throughout the flow.
-
Term: NoSlip Condition
Definition:
Condition in fluid mechanics indicating the velocity of fluid at a boundary surface is equal to that of the surface.
-
Term: Interface Boundary Conditions
Definition:
Conditions that apply at the boundary between two different fluids in contact, ensuring continuity in velocity and shear stress.