Navier-Stokes Equation part 2
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Continuity Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today's class revolves around the continuity equations for incompressible flow. Remember, these equations ensure that mass is conserved in our fluid systems.

What does it mean for a flow to be incompressible, exactly?

Great question! An incompressible flow means the fluid's density remains constant. For our equations, we say that the divergence of the velocity field is zero.

How do we express this mathematically?

We write it as \( \nabla \cdot v = 0 \). This divergence equation is fundamental to understanding how fluid mass cannot 'disappear' in a closed system.
Linear Momentum Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s delve into the linear momentum equations. They describe how forces relate to acceleration in fluid contexts.

What are the primary forces we consider?

We consider gravitational forces, pressure forces, and viscous forces. Each plays a crucial role in how fluids move.

Can we simplify these equations?

Absolutely! For example, if viscosity approaches zero, we can reduce our equations to the Euler equations, which makes solutions simpler.
Assumptions in Fluid Dynamics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

The key assumptions for our equations include that we use Newtonian fluids and isothermal conditions. Why do you think these are important?

They help ensure the viscosity remains constant, right?

Exactly! A constant viscosity allows us to formulate more straightforward solutions to our equations.

What happens if our assumptions are wrong?

If they're incorrect, we might misinterpret our fluid behavior, leading to poor designs or analyses in real applications. Always check your boundary conditions!
Practical Applications of Fluid Concepts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's consider practical applications of what we've learned. Can anyone think of an example in biology?

How about blood flow in arteries? Blockages could create complex flow patterns.

Perfect! Blood flow can be symmetric or asymmetric, significantly affecting pressure and velocity distributions. Understanding these helps in medical fields.

And what about rivers? They must also have zones where flow is constrained!

Exactly! These scenarios illustrate how fluid mechanics is essential across various fields, from engineering to biology.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Part two of the Navier-Stokes equation discussion delves into the linear momentum equations and continuity equations for incompressible fluids. Key assumptions, including Newtonian fluid behavior and isothermal conditions, are explained, along with methods to simplify complex equations for practical applications in fluid mechanics.
Detailed
Detailed Summary
In this section, Professor Dutta expands on the Navier-Stokes equations, focusing on four critical equations governing fluid mechanics: the four equations of mass conservation and linear momentum. The discussion emphasizes the assumptions made during the derivations, particularly for incompressible Newtonian fluids, where density remains almost constant and the viscosity is a constant under isothermal conditions.
Key points include:
- Continuity Equations: The equations of continuity for incompressible flow are expressed in vector forms, showcasing the divergence of the velocity field as a crucial aspect of mass conservation.
- Linear Momentum Equations: An analysis of the linear momentum equations in vector forms demonstrates the relationship between mass, acceleration, and forces acting on fluid elements, including gravity, pressure, and viscous stress components.
- Approximations and Simplifications: Strategies for approximating the Navier-Stokes equations are discussed, including scenarios where viscosity is negligible, leading to the Euler equations. The significance of these simplifications in practical applications, such as deriving Bernoulli's equations from Euler's, is highlighted.
- Flow Conditions: The section presents scenarios of symmetric and asymmetric flow features, including fluid flow in biological contexts (like artery blockages) and natural systems (like river flows), cultivating an understanding of how different parameters affect fluid dynamics.
- Finally, Professor Dutta urges students to embrace the nuances of fluid mechanics beyond mere equation solving, emphasizing the importance of comprehending fluid behaviors and their applications in various fields.
Youtube Videos



![[Fluid Dynamics: Equation] Is Navier Stokes equation correct? Part 2, Solutions](https://img.youtube.com/vi/loBOzxiqQas/mqdefault.jpg)

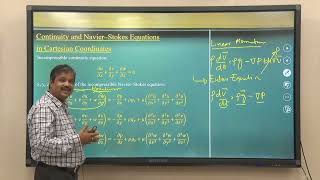



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equations
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Good morning. Let us start today's class on Navier-Stokes equations. In the last class, we have derived the Navier-Stokes equations, which is the four equations, mass conservation equations and the linear momentum equations. As we have the four equations, as well as we have four dependent variables like velocity field u, v, w, and the pressures for incompressible flow. So, solving that equations you can get the solutions velocity field and the pressure field for incompressible Newtonian fluids.
Detailed Explanation
In this section, the professor introduces the Navier-Stokes equations, which are vital for understanding fluid mechanics. These equations consist of four critical equations: mass conservation and linear momentum equations. The variables involved include the velocity components in three dimensions (u, v, and w) and pressure. For incompressible Newtonian fluids, solving these equations helps determine the velocity and pressure fields of the flow system.
Examples & Analogies
Think of the Navier-Stokes equations like the rules for playing a complex board game. Just as players must follow certain rules to achieve a goal, fluid particles must obey these equations to accurately depict their behavior in motion, such as how water flows through a pipe.
Continuity Equation for Incompressible Flow
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Please always have a remember what are the assumptions we have when you are deriving basic fluid equations today as we are discussing about Navier-Stokes equations. Today I will talk about the Navier-Stokes equations, how we do the approximations of Navier-Stokes equations for a simplified fluid flow with giving a series of illustrations that how we can simplify these Navier-Stokes equations.
Detailed Explanation
This section emphasizes the importance of understanding the assumptions behind the Navier-Stokes equations before proceeding with their applications. The continuity equation, which ensures mass conservation, must be considered. The professor mentions that approximations will be discussed to simplify the equations for fluid flow analysis, which is essential for practical engineering applications.
Examples & Analogies
Consider a busy highway full of cars. The continuity equation is like managing traffic flow: if one lane gets congested (mass doesn't flow through), adjustments must be made in other lanes to maintain overall traffic balance, similar to how mass conservation maintains flow in fluids.
Linear Momentum Equations
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look at the next the linear momentum equations as we have derived this is linear momentum equations in vector forms. So, in vector forms it is comes like rho So, it is the accelerations part is equal to is rho g grade p pressures into mu Laplace operators of velocity field.
Detailed Explanation
This chunk discusses linear momentum equations presented in vector form. The equations reflect the balance of forces acting in a fluid. The quantity 'rho' refers to density, while 'g' represents gravitational influence, and 'p' is pressure. The Laplacian operator applies to the velocity field, indicating how velocity gradients influence the flow. Understanding these equations helps in analyzing how fluids respond to applied forces such as pressure and gravity.
Examples & Analogies
Imagine a soccer ball on a field, where the ball (fluid) experiences forces when kicked (pressure) and pulled (gravity). The linear momentum equations would describe how the ball reacts to these forces, just as they describe the behavior of fluids in various conditions.
Assumptions in Fluid Flow
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We have considered the isothermal case the mu is a constant, we have considered incompressible flow where the rho is a constant. So, all the three assumptions are giving us equations which expanded in the x directions.
Detailed Explanation
In this part, the professor summarizes key assumptions made when working with fluid flow. These include treating the dynamic viscosity (mu) as constant, assuming incompressible flow (constant density, rho), and looking at specific directions while expanding the equations. These assumptions are crucial, as they simplify complex fluid dynamics, making it easier to apply the Navier-Stokes equations in practical scenarios.
Examples & Analogies
These assumptions can be compared to simplifying a recipe by assuming perfect kitchen conditions — using constant temperature and quantity of ingredients makes the resulting dish predictable, just as the assumptions in fluid flow make calculations straightforward and manageable.
Conditions for Simplification
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If I can say that this is becomes 0 then it is for me it is easy for integrating these terms because these are easy to integrate it along this field they are.
Detailed Explanation
The section discusses how certain conditions, which essentially cause specific terms in the equations to equal zero, make it easier to integrate and solve the equations. By identifying conditions where viscous effects are negligible, the complexity of the equations can be reduced, allowing for more intuitive models like the Euler equations to be used instead of the full Navier-Stokes.
Examples & Analogies
Consider a ski slope: if there’s no friction between the skis and the snow (like neglecting viscosity), the skier can glide down effortlessly without complex calculations. This is analogous to simplifying fluid equations and focusing only on major interactions, simplifying the problem greatly.
Euler Equations and Flow Conditions
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, if you look at these terms, if I look at this d v by d t, if I just expand it I will have a components is a local accelerations component which is with respect to time and I will have a components V dot grade.
Detailed Explanation
This segment elaborates on the Euler equations, which arise under conditions where viscous effects are minimal or ignored. These equations help describe fluid motion without complexities introduced by viscosity and are particularly useful in theoretical scenarios, such as ideal flow conditions where the fluid behaves as a perfect fluid.
Examples & Analogies
Imagine sailing on a calm sea where the wind is steady and there are no waves. The boat moves smoothly and predictably — this situation mimics ideal flow in fluids, where the complex factors like friction can be considered negligible.
Key Concepts
-
Mass Conservation: The principle stating that mass cannot be created or destroyed in an isolated system.
-
Velocity Field: The distribution of velocity in a fluid, represented spatially.
-
Viscous Forces: Forces resulting from the internal friction in the fluid, dependent on the fluid's viscosity.
-
Boundary Conditions: Constraints that define how the fluid interacts with its surroundings.
Examples & Applications
Blood flow in arteries can be analyzed using the Navier-Stokes equations, especially regarding blockages or diseases.
River flow patterns can illustrate both symmetric and asymmetric flow behaviors influenced by natural restraints like bridges.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
For flow that's incompressible, wake up and remember, divergence is zero, like hot in December.
Stories
Imagine driving on a road where the cars never change their speed; that’s like incompressible flow: they stay within their lanes, constant as they move.
Memory Tools
To remember the assumptions for Navier-Stokes: 'N.I.C.E.' - Newtonian, Incompressible, Constant viscosity, Equilibrium conditions.
Acronyms
Remember 'MVP' for Momentum, Viscosity and Pressure effects in fluid dynamics.
Flash Cards
Glossary
- NavierStokes Equations
A set of equations that describe the motion of fluid substances, combined with the principles of mass conservation, momentum conservation, and energy conservation.
- Incompressible Flow
A flow regime where the fluid density remains constant, leading to a divergence of the velocity field being zero.
- Continuity Equation
An equation that expresses mass conservation in fluid dynamics, requiring that the mass flow rate remains constant in a closed system.
- Newtonian Fluid
A class of fluids with a constant viscosity, where the shear stress is directly proportional to the shear rate.
- Euler Equations
The simplified equations derived from the Navier-Stokes equations under assumptions of negligible viscosity.
Reference links
Supplementary resources to enhance your learning experience.
