Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Tidal Energy
Unlock Audio Lesson
Good morning, class! Today, we will explore the fascinating world of tidal energy harvesting. Can anyone tell me what tidal energy is?
Tidal energy is the energy generated from the movement of tides in the ocean.
Exactly! Tidal energy is derived from the gravitational interactions between the Earth, the moon, and the sun. It is a renewable source of energy that's predictable and consistent. Can you think of any advantages of using tidal energy?
Yes, it's more reliable than solar and wind energy since tides are very predictable.
Correct! Tidal energy has the potential for a continuous energy supply. Let's dive deeper into how this energy is harvested.
Mechanics of Tidal Energy Harvesting
Unlock Audio Lesson
In tidal energy harvesting, turbines are placed in tidal flows. Who can explain how these turbines work?
They convert the kinetic energy from moving water into mechanical energy, and then into electricity.
Right! The efficiency of these turbines depends significantly on their interaction with the tidal flow, which we can analyze using the Navier-Stokes equations. Can anyone tell me what these equations govern?
They govern the motion of fluid substances.
Absolutely! They model how fluids behave under various conditions. Understanding these equations is key to optimizing turbine designs.
Simplifications of the Navier-Stokes Equations
Unlock Audio Lesson
To analyze the flow around the turbines, we often simplify the Navier-Stokes equations. Can anyone suggest why simplifications might be necessary?
Because the full equations are very complex, and simplifying them can make calculations more manageable.
Exactly! When working with Newtonian fluids in incompressible flow, we can assume certain factors, which makes our calculations easier. What assumptions do we typically use?
We assume constant density and that viscosity is uniform.
Very well! These assumptions lead us to a more simplified model that we can work with in designing tidal energy systems.
Boundary Conditions in Tidal Energy Systems
Unlock Audio Lesson
When designing tidal energy systems, what kind of boundary conditions do you think we need to consider?
We need to think about the interface between the water and the turbine as well as the seabed.
Good point! We also consider no-flow boundary conditions at the seabed. Why is this important?
Because it helps us define how the water interacts with the turbine effectively.
Exactly! Boundary conditions play a crucial role in determining the efficiency and effectiveness of tidal energy systems.
Real-World Applications of Tidal Energy
Unlock Audio Lesson
Can anyone give me an example of where tidal energy is being harvested today?
The La Rance Tidal Power Station in France!
That's a great example! It has been in operation since 1966. Tidal energy has a potential to contribute significantly to our energy needs. What do you think is key for its future expansion?
If we can improve turbine efficiency and reduce costs for installation.
Spot on! Technological advancements will be crucial for making tidal energy more economically viable in the future.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses tidal energy as a renewable resource, illustrating how tidal energy harvesting works through turbines placed in tidal flows. It examines the significance of Newtonian fluids, the Navier-Stokes equations, and the simplifications necessary to understand tidal energy systems.
Detailed
Tidal Energy Harvesting
Tidal energy harvesting leverages the power of ocean tides, which are caused by gravitational forces from the moon and sun. This section illustrates how turbines can be installed in tidal flows to convert kinetic energy into electricity, highlighting both the physics and engineering involved. The interaction between tidal water and the turbines can be analyzed using fluid mechanics, specifically the Navier-Stokes equations which govern fluid motion.
The Navier-Stokes equations, under certain assumptions such as incompressibility and Newtonian fluid behavior, form the basis for understanding fluid dynamics in energy harvester applications. Simplifications of these equations help streamline the calculations necessary for designing effective tidal energy systems. Understanding the flow dynamics and utilizing computational fluid dynamics (CFD) tools are crucial for maximizing energy extraction.
The deliberation also includes essential boundary conditions for analyzing flow around turbines, offering insights into real-world applications of tidal energy systems.
Youtube Videos
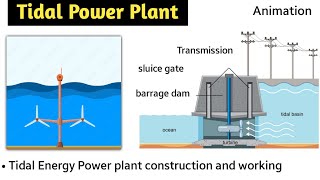
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Tidal Energy Harvesting
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let me give a simple example of the tidal energy, which nowadays very famous for the cases of getting the renewable energies. The tidal energy harvesters are nowadays very interesting components are there.
Detailed Explanation
Tidal energy harvesting involves capturing energy generated by the rise and fall of tides. This method of energy production is gaining popularity as a renewable energy source. Tidal energy harnesses the kinetic and potential energy from the ocean's tides, which are caused by the gravitational interactions between the Earth, moon, and sun. As tides rise and fall, they can be used to turn turbines and generate electricity.
Examples & Analogies
Think of tidal energy like a water wheel in a river. Just as the flowing river turns the wheel to produce energy, the movement of the tides can turn turbines placed underwater, generating electricity that can power homes and businesses.
How Tidal Energy Harvesters Work
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Like for examples, you will have a bed. You construct a turbine and the flow comes like this. This is the tidal which comes from these, this is the upstream, this is the downstream and you try to look at this is the air, this is the waters, You try to solve these problems using computational fluid dynamics or you try to solve analytically to know it how much of energy harvesters will be there if I just put a turbine below a sea level where the tidal waves will rotate these turbines and we can harvest the energy.
Detailed Explanation
In a tidal energy harvesting system, turbines are placed in water bodies where tidal movements occur. As the water level rises and falls with the tides, it creates a flow of water that can turn these turbines. When the turbines spin, they generate electricity. Computational Fluid Dynamics (CFD) may be used to model and analyze these flow patterns, optimizing the design and placement of turbines to maximize energy capture.
Examples & Analogies
Imagine you’re at the beach, watching waves crash. If you had a series of small windmills along the shore that were turned by the waves and tides, each time a wave hits or recedes, they would spin and produce energy.
Importance of Boundary Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can use the no flow boundary condition. What are the boundary conditions we are imposing at the interface between air and waters? This is the interface between the air and waters that is what is the free surface boundary and what is the boundary conditions we are applying here.
Detailed Explanation
Boundary conditions are crucial in fluid mechanics, especially in tidal energy systems. They define how fluid (water and air) interacts with structures (turbines or beds). The 'no flow boundary condition' means that at the bottom of the sea bed where the turbines are, no water will 'flow' through it; instead, the water will only move around it. Additionally, the conditions at the air-water interface (the free surface) must be carefully defined to understand the behavior of water as it interacts with air.
Examples & Analogies
Consider the boundary of a swimming pool where water meets the pool edge. Imagine how the water behaves as you swim; vital here is that at the edge, water does not bypass the wall. This analogy helps understand how boundary conditions work in tidal energy systems.
Simplifying Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We will not look it to solve this Navier-Stokes equations as it because it is a non-linear two-dimensional equations. We try to simplify these equations. That is what I will give you some of the examples how we can simplify these equations.
Detailed Explanation
The Navier-Stokes equations describe how fluids move and are inherently complex due to their non-linear nature. In the context of tidal energy harvesting, it is often necessary to simplify these equations to make them more manageable for analysis. This might involve assumptions such as steady flow, incompressibility, and ignoring certain forces based on their insignificance compared to others.
Examples & Analogies
Think of it like simplifying a recipe. If you're making a complex dish but only have a limited set of ingredients, you might decide to omit some steps or ingredients to make it easier and quicker to prepare. Similarly, simplifying equations helps us focus on the most important factors affecting tidal energy harvesting.
Conclusion and Future Prospects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Always you can draw the velocities which is very interestingly here that if there is a interface and if I am to draw the velocity distributions the in air I will have a very fast the gradient to support these boundary conditions But in case of waters, we will have the less because this is what is 50 times lesser than that.
Detailed Explanation
Understanding the velocity distributions at the interface of air and water is crucial for optimizing tidal energy systems. The disparity in velocity between water and air implies that different approaches may be needed for energy generation. For example, the greater resistance of water compared to air affects how effectively turbines can generate energy in tidal flows. As we advance, the understanding of these complex interactions will lead to improved designs for tidal energy harvesting systems and greater efficiency.
Examples & Analogies
Imagine trying to blow up a balloon partially submerged in water. The resistance of the water makes it much harder to inflate in comparison to blowing air directly into the balloon above water. This analogy helps illustrate how different mediums interact and influence energy generation in tidal systems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Tidal Energy: Energy from the movement of ocean tides.
-
Navier-Stokes Equations: Equations governing fluid motion and dynamics.
-
Newtonian Fluid: Fluids with constant viscosity under shear stress.
-
Boundary Conditions: Essential parameters that define the behavior of fluids in a system.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of tidal energy harvesting includes the La Rance Tidal Power Station in France, one of the first tidal power plants.
-
In tidal energy systems, turbines are often used to harness energy by converting moving water energy into mechanical energy.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Tides rise and fall, energy calls, turbines harness all, as nature enthralls.
📖 Fascinating Stories
-
Imagine a giant seesaw – with the moon on one end and the sun on the other – lifting the ocean's waves, making tidal energy flow.
🧠 Other Memory Gems
-
NAB: Newtonian, Assumption of Constant Density, Boundary Dependence – key concepts for fluid systems.
🎯 Super Acronyms
T.E.A.R
- Tidal Energy and Renewable - a reminder of the sustainability of tidal energy resources.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Tidal Energy
Definition:
Energy derived from the gravitational effects of the moon and the sun on Earth's oceans, manifested in the movement of tides.
-
Term: NavierStokes Equations
Definition:
Fundamental equations that describe the motion of fluid substances, capturing the relationships between velocity, pressure, and external forces.
-
Term: Newtonian Fluid
Definition:
A fluid whose viscosity remains constant regardless of the shear rate, typically characterized by a linear relationship between shear stress and shear rate.
-
Term: Boundary Conditions
Definition:
Conditions applied at the boundaries of a system to define how flows interact with surfaces, crucial in fluid dynamics modeling.
-
Term: Kinetic Energy
Definition:
The energy possessed by an object or fluid due to its motion.