Future Value of an Annuity (FVA)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Future Value of Annuity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll explore the Future Value of an Annuity, or FVA. It helps us determine how much a series of regular payments will grow over time due to interest. Remember, money grows over time, and this concept captures that essence!

Is FVA the same as just calculating the future value of a single amount?

Not quite! FVA deals with multiple payments made over several periods, whereas a single amount's future value looks at one initial sum. FVA takes into account the effects of regular contributions.

Can you give us an example of where we might use this FVA concept?

Certainly! Think about saving for retirement. If you contribute a fixed amount to your retirement fund monthly, FVA helps project how much your total savings will be worth upon retirement!

So if I contribute ₹2000 every month, how would FVA help me understand my savings?

By applying the FVA formula, you could estimate how much those contributions could grow depending on your interest rate and how long you plan to save.

In summary, FVA is a powerful tool for future planning. Keep in mind the formula: $FVA = PMT \times \frac{(1 + r)^n - 1}{r}$. Each part represents a critical element in understanding your future finances.
Breakdown of the FVA Formula
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's break down the FVA formula. We have three key components: PMT, r, and n. PMT stands for the fixed amount you pay regularly.

What exactly is 'r'? Is it just the basic interest rate?

Great question! 'r' is the interest rate per period. If you have an annual interest rate but are making monthly contributions, you'd need to convert that annual rate to a monthly rate.

And 'n'? How is that different from 'r'?

'n' is the total number of payment periods. If you plan to save for 10 years and make monthly contributions, 'n' would be 10 years times 12 months, equaling 120 periods!

I see! So each component plays a specific role in determining the future value!

Exactly! Understanding these components will help you apply the FVA formula correctly in various financial scenarios.

Could we calculate an example together?

Absolutely! Let's take PMT as ₹2000, an interest rate of 5% per year, and calculate for 10 years. Remember, we convert the interest rate for our monthly periods and find 'n' as 120. Let's plug in these values later!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The FVA formula is critical for understanding how regular payments accumulate over time, using interest. This section explains its components, including periodic payments, interest rates, and the number of periods, and provides applications in financial planning and investment analysis.
Detailed
Future Value of an Annuity (FVA)
The Future Value of an Annuity (FVA) is an important financial concept that calculates the total future value of a series of equal payments made at regular intervals, considering a specific interest rate. The formula for calculating FVA is:
$$FVA = PMT \times \frac{(1 + r)^n - 1}{r}$$
Where:
- PMT is the periodic payment made,
- r is the interest rate for each period,
- n is the total number of periods.
This formula helps individuals and businesses understand how much their consistent investments will grow over time.
Significance in Financial Planning
By understanding FVA, professionals—especially students in finance and tech—can make informed decisions about savings, retirement plans, and investments. Knowing the future value of regular contributions aids in budgeting, forecasting, and investment analysis.
Youtube Videos



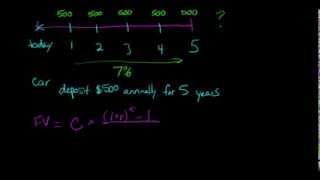





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Future Value of an Annuity
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
FVA = PMT × ¿
Where:
- PMT = periodic payment
- r = interest rate
- n = number of periods
Detailed Explanation
The Future Value of an Annuity (FVA) can be understood as the total value of a series of equal payments made at regular intervals in the future, after accounting for interest. The formula provided shows that the FVA is calculated by multiplying the periodic payment (PMT) by a factor that considers the interest rate (r) and the number of periods (n) over which the payments are made. Essentially, this formula captures how the value of these payments grows over time due to interest.
Examples & Analogies
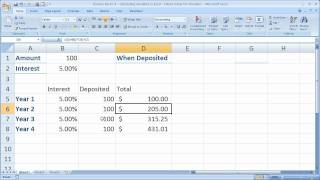
Imagine you are saving money for a vacation by putting away a fixed amount each month. If you save ₹1,000 every month in an account that earns a 5% annual interest rate, at the end of several months, the total amount you've saved will not just be the sum of all your deposits; it will also include the interest earned on those deposits over time. This added value from interest is what the Future Value of an Annuity measures.
Components of the FVA Formula
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Where:
- PMT = periodic payment
- r = interest rate
- n = number of periods
Detailed Explanation
The FVA formula consists of three main components: PMT, r, and n. Here's a deeper look at each component:
1. PMT (Periodic Payment): This is the fixed amount that you will pay or receive at regular intervals. For instance, if you decide to save ₹1,000 every month, then your PMT is ₹1,000.
2. r (Interest Rate): This represents the annual interest rate applied to the payments. It's crucial because the higher the interest rate, the more your savings will grow over time. If your savings account offers 5% annual interest, r will be 0.05 in the formula.
3. n (Number of Periods): This indicates how many times you make those payments. If you are saving for three years and make monthly payments, n will equal 36 (12 months x 3 years). This is important because each payment earns interest for a differing amount of time, depending on when it is made.
Examples & Analogies
Consider a garden where you plant flowers (PMT) every month (the annual interest rate influences how well they grow). If you regularly water them (the cash flow) and they receive sunlight (the interest accumulated), they will bloom beautifully (future value) over the growing season (the number of periods). Just like flowers, the growth of your savings depends on consistent contributions, the right conditions (interest rates), and time.
Key Concepts
-
FVA Formula: The formula used to compute the future value of periodic payments.
-
Components of FVA: PMT, r, and n are essential for calculating FVA.
-
Difference Between FVA and FV: FVA applies to multiple payments while FV usually applies to a single sum.
Examples & Applications
If you save ₹5000 every year at an interest rate of 7% for 5 years, the FVA can help you calculate how much this will total in 5 years.
For a monthly investment of ₹1000 for 10 years at an interest rate of 6% compounded monthly, FVA helps project future savings.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Saving time, to be wise, FVA keeps future dreams in eyes!
Stories
Imagine a squirrel collecting nuts monthly. At year-end, each nut becomes worth twice thanks to interest—this is what FVA shows!
Memory Tools
To remember FVA components: 'PMT, r, n', think 'Payments Mean Time's returns'.
Acronyms
For FVA
'P' for Payments
'R' for Rate
'N' for Number of periods to create your fate.
Flash Cards
Glossary
- Future Value of Annuity (FVA)
The total future value of a series of equal payments made at regular intervals, considering a specific interest rate.
- PMT
The amount of each payment made in an annuity.
- Interest Rate (r)
The rate at which money grows over time, expressed as a percentage.
- Number of Periods (n)
The total number of payment intervals in which payments are made.
Reference links
Supplementary resources to enhance your learning experience.
