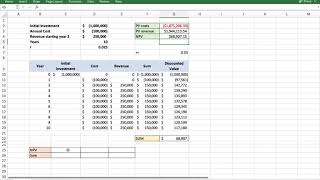
Present Value (PV)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Present Value
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will be discussing Present Value, or PV. Can anyone tell me why money today is worth more than the same amount in the future?

Because of interest rates, right? We could invest it and earn more.

Exactly! That's called earning capacity. We can use a formula to quantify this idea. The formula for PV is \[PV = \frac{FV}{(1 + r)^t}\]. Who can break down what each part of this formula means?

FV stands for Future Value, which is the amount we will receive later, and r is the interest rate.

And t is the number of years until we receive that amount.

Great! This formula allows us to calculate how much future money is worth today. Remember: 'Present Value is the Future Value brought to today.'

So, if I understand, the longer I wait to receive money, the less it's worth today?

Absolutely! Time diminishes the value of future money due to uncertainty and lost investment opportunities. Let's move to a practical example.
Practical Calculation of PV
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's say you expect to receive ₹10,000 five years from now and the interest rate is 10% per annum. How would we calculate the Present Value?

We'd plug it into the formula! So, PV = \[\frac{10,000}{(1 + 0.10)^5}\]

Right! Now, can anyone calculate that for me?

I think it’s around ₹6,209.

Correct! That means if you want to receive ₹10,000 in 5 years at a 10% interest rate, you would need to have approximately ₹6,209 today to achieve that goal. This practical application is vital for anyone working in finance.

So, it's essential to calculate PV for investments too, right?

Exactly! Assessing the present value of future cash flows helps investors understand whether to pursue an investment. Always remember to consider the time component!
Importance of PV in Business Decisions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss why understanding Present Value is critical in business decisions. Why do you think that is?

It helps in deciding if an investment is worth it today.

Wonderful! By calculating PV, businesses can evaluate potential projects and their profitability. Can someone provide an example of how PV might be used?

If a startup expects to make a profit of ₹100,000 after 3 years, they need to calculate its PV to understand if that’s worth investing in now.

Exactly! And they would factor in the discount rate to determine if that profit is acceptable today. Remember, decisions based on future cash flow depend on how much they are worth right now.

So, if PV is lower than the investment cost, it's better to reconsider?

Spot on! Understanding the time value of money through PV calculations is vital for making informed financial decisions.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The concept of Present Value (PV) quantifies the current equivalent of a sum of money that will be received in the future, discounted at a specified interest rate. Understanding PV is crucial for assessing future cash flows in finance, helping to determine their value in today's terms.
Detailed
Present Value (PV)
Present Value (PV) refers to the current worth of a sum of money to be received in the future, discounted at a certain interest rate. The formula to calculate PV is:
\[
PV = \frac{FV}{(1 + r)^t}
\]
Where:
- FV is the future value of the money to be received.
- r is the interest rate (or discount rate).
- t is the time period in years until the amount is received.
This concept represents the foundational idea that receiving money in the future is worth less than having the same amount today due to its potential earning capacity. For business decisions, understanding PV helps in investments, capital budgeting, and financial forecasting.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Present Value
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The current worth of money to be received in the future.
Detailed Explanation
Present Value (PV) is a financial concept that helps us understand how much a future sum of money is worth today. It takes into account the effects of interest rates on the value of money over time. If you expect to receive a certain amount in the future, its value in today's terms will be less due to potential earning capacity of that amount if invested. Essentially, PV allows you to assess what future money is worth in today's terms, making it a crucial tool in financial decision-making.
Examples & Analogies
Imagine you are promised ₹10,000 two years from now. If you could invest that money today at an interest rate of 10%, it would be worth more than ₹10,000 (as it will grow over time). To understand how much ₹10,000 in two years is worth right now, consider this: receiving money now can allow you to earn interest, so that prospective future money needs to be discounted to reflect its present value.
Present Value Formula
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
PV = FV / (1 + r)^n
Detailed Explanation
The formula for calculating Present Value (PV) is: PV = FV / (1 + r)^n. Here, 'PV' is the present value we want to find, 'FV' is the future value of the money we expect to receive, 'r' is the rate of interest (expressed as a decimal), and 'n' is the number of years until the payment or cash flow is received. This formula demonstrates how future amounts must be adjusted according to the time and interest rate to reflect their value today.
Examples & Analogies
Let’s say you expect to receive ₹10,000 in two years (FV). If the interest rate is 10% (or 0.10 as a decimal), you would plug these values into the formula: PV = 10,000 / (1 + 0.10)^2. This simplifies to PV = 10,000 / 1.21, which equals about ₹8,264. This means that the ₹10,000 to be received in two years is worth about ₹8,264 today, given a 10% interest rate.
Example of Present Value Calculation
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example: If ₹10,000 is invested at 10% interest for 2 years: FV = 10,000 × (1 + 0.10)^2.
Detailed Explanation
Using the present value formula, let’s calculate how much ₹10,000 in the future is worth today. First, we calculate the future value for 2 years at a 10% interest rate. The calculation follows: FV = 10,000 × (1 + 0.10)^2. Calculating this gives: FV = 10,000 × 1.21 = ₹12,100. Now, to find the present value using the formula, we reverse the process. We want to find PV such that PV = FV / (1 + r)^n. We plug in our FV of 12,100, r as 0.10, and n as 2, leading to: PV = 12,100 / (1.21), essentially showing how we arrived at our earlier calculations.
Examples & Analogies
Think of planning a vacation that you can take in two years. If you know you'll need ₹10,000 to have a comfortable trip, you can start saving now. If you invest that money today with a good interest rate, you’re not just storing funds; you’re enabling those funds to grow. By the time the vacation arrives, that amount could actually be less than what you need in present value terms. So by calculating present value, you can set a meaningful savings goal today to meet your future needs.
Key Concepts
-
PV Calculation: Present Value is calculated using the formula PV = FV / (1 + r)^t.
-
Importance of PV: Knowledge of PV informs business decisions regarding future cash flows and investment evaluations.
-
Impact of Time: The value of future money decreases over time, which is quantified in PV calculations.
Examples & Applications
If you expect to receive ₹5,000 in 3 years at a discount rate of 8%, the Present Value can be calculated as follows: PV = 5000 / (1 + 0.08)^3, which equals approximately ₹3,957.
For an investment that promises to return ₹50,000 in 10 years with a 12% discount rate: PV = 50000 / (1 + 0.12)^10, resulting in a PV of roughly ₹15,822.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Future cash, it sounds great; but PV tells you it's less in rate.
Stories
Imagine finding a treasure chest of gold coins that you can open in five years. PV is like calculating today's value of that treasure based on what you could earn investing the coins now.
Memory Tools
To remember PV: P for Present, V for Value, and 'D' for Discounting future money.
Acronyms
PV
Prepare Values
meaning prepare your values for today’s context.
Flash Cards
Glossary
- Present Value (PV)
The current worth of an expected future sum of money, discounted at a specified interest rate.
- Future Value (FV)
The amount of money that will be received or owed in the future, typically calculated with interest.
- Interest Rate (r)
The percentage at which money will earn or incur interest over a period.
- Discount Rate
The interest rate used to discount future cash flows to their present value.
- Time Period (t)
The duration for which the money is invested or borrowed, expressed in years.
Reference links
Supplementary resources to enhance your learning experience.
