Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Algebraic Multiplicity
Unlock Audio Lesson
Today, we're going to explore algebraic multiplicity. Can anyone tell me what they think it means?
Is it how many times an eigenvalue shows up in the characteristic polynomial?
Exactly, that's right, Student_1! The algebraic multiplicity of an eigenvalue λ is the number of times λ appears as a root of that characteristic polynomial. It's denoted as AM(λ). This counts the total multiplicity including repeated eigenvalues.
So, if λ appears twice, AM(λ) would be 2?
Correct! Now, remember that the AM helps us understand the structure of the matrix. Let's review a mnemonic: 'A Count of Roots' where A stands for Algebraic and Count reminds us it's tied to counting appearances.
Exploring Geometric Multiplicity
Unlock Audio Lesson
Now that we discussed algebraic multiplicity, let’s move on to geometric multiplicity. Who knows what it is?
Is it related to the space formed by eigenvectors?
Great connection, Student_3! Geometric multiplicity, or GM, is the dimension of the eigenspace corresponding to the eigenvalue λ. It tells us how many linearly independent eigenvectors we can find for that eigenvalue.
So if GM is 2, it means there are two linearly independent eigenvectors?
Exactly, Student_4! And remember our acronym: 'Geometric Gives Dimension.' This helps us recall that geometric multiplicity relates to the dimension of eigenspaces.
The Relationship Between AM and GM
Unlock Audio Lesson
Let’s discuss how algebraic multiplicity and geometric multiplicity relate to each other. Who can tell me the property we should remember?
Is it the inequality 1 ≤ GM(λ) ≤ AM(λ)?
Absolutely right, Student_1! This tells us that geometric multiplicity is always less than or equal to algebraic multiplicity. So if you ever encounter GM that is less than AM, that indicates certain properties of the matrix.
Does this mean if GM equals AM, the matrix is diagonalizable?
Exactly! If GM equals AM for all eigenvalues, the matrix is diagonalizable, which means we can write it in a diagonal form. Let's keep our mnemonic 'AM Equals GM Means Diagonalizable' to remember this!
Implications in Linear Algebra
Unlock Audio Lesson
Finally, let’s consider the implications. Why is understanding AM and GM significant in real-world applications?
I think it helps in understanding the behavior of matrices in dynamic systems, right?
Exactly! In fields like civil engineering, knowing the multiplicities helps in modal analysis and understanding vibrations. Recapping: AM helps us count roots while GM reveals the structure of eigenvectors.
So if a matrix isn't diagonalizable, it might complicate the analysis?
Precisely, Student_4! Non-diagonalizable systems may introduce challenges in predicting behavior. So remembering these concepts is key!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Algebraic multiplicity refers to the number of times an eigenvalue appears in the characteristic polynomial, while geometric multiplicity is the dimension of the corresponding eigenspace. Understanding these concepts is vital, as the relationship between them informs whether a matrix is diagonalizable.
Detailed
Algebraic and Geometric Multiplicity
In linear algebra, every eigenvalue of a matrix has two important characteristics: algebraic multiplicity (AM) and geometric multiplicity (GM).
- Algebraic Multiplicity (AM): This is defined as the number of times an eigenvalue BB appears as a root of the characteristic polynomial of the matrix.
- Geometric Multiplicity (GM): This refers to the dimension of the eigenspace associated with the eigenvalue, which is equivalent to the number of linearly independent eigenvectors corresponding to that eigenvalue.
An important property connecting these two multiplicities is expressed in the inequality:
1 ≤ GM(BB) ≤ AM(BB)
If for all eigenvalues GM equals AM, the matrix is said to be diagonalizable, which means it can be expressed in a simpler form as a diagonal matrix. Understanding the multiplicities is crucial for applying linear algebra in various fields, including engineering, as it provides insights into the structure and behavior of linear transformations.
Youtube Videos
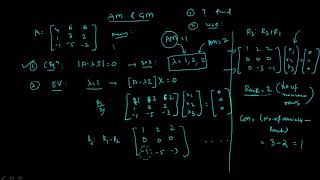
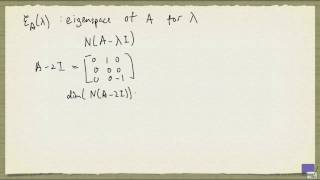
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Algebraic Multiplicity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For each eigenvalue λ:
- Algebraic multiplicity (AM): Number of times λ appears as a root of the characteristic polynomial.
Detailed Explanation
The algebraic multiplicity of an eigenvalue is defined as the number of times that eigenvalue appears in the characteristic polynomial of a matrix. This polynomial is obtained when we perform the determinant operation on the matrix subtracted by λ times the identity matrix. Each unique eigenvalue has an associated algebraic multiplicity, indicating how many roots in the polynomial equation correspond to that eigenvalue.
Examples & Analogies
Consider a school class where a particular student represents an eigenvalue. If that student is listed multiple times in the class register due to backup lists or attendance records, then the number of times they appear reflects their algebraic multiplicity.
Definition of Geometric Multiplicity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Geometric multiplicity (GM): Dimension of the eigenspace E_λ, i.e., number of linearly independent eigenvectors for λ.
Detailed Explanation
The geometric multiplicity of an eigenvalue is determined by the dimension of its corresponding eigenspace. The eigenspace consists of all eigenvectors associated with the eigenvalue and includes zero vectors. The geometric multiplicity is directly related to the number of linearly independent eigenvectors for that specific eigenvalue. For instance, if there are three independent eigenvectors for a certain eigenvalue, its geometric multiplicity is 3.
Examples & Analogies
Imagine a workshop where multiple students (eigenvectors) can independently create their own unique designs (solutions) using the same materials (eigenvalue). The number of unique designs they can make independently defines the geometric multiplicity.
Important Property Relating AM and GM
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Important Property:
1 ≤ GM(λ) ≤ AM(λ)
Detailed Explanation
An important relationship exists between the algebraic multiplicity and geometric multiplicity of eigenvalues. This property states that the geometric multiplicity of any eigenvalue is always at least 1 (since there is at least one eigenvector associated with it) and can never exceed the algebraic multiplicity of that eigenvalue. Thus, we can say that GM is at least 1 and cannot be greater than AM.
Examples & Analogies
Think of a concert where artists (eigenvectors) are asked to sing songs (eigenvalues). The total number of songs sung (algebraic multiplicity) indicates how many unique performances were executed, whereas the number of artists independently performing (geometric multiplicity) cannot exceed the total number of songs available. There must be at least one artist to perform songs, reflecting the relationship!
Diagonalizability Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If GM=AM for all eigenvalues, then the matrix is diagonalizable.
Detailed Explanation
A matrix is said to be diagonalizable if it has enough linearly independent eigenvectors to form a basis for the entire vector space. If for every eigenvalue, the geometric multiplicity equals the algebraic multiplicity, then this condition is satisfied, allowing the matrix to be represented in its diagonal form. This property greatly simplifies matrix operations and analysis.
Examples & Analogies
Consider a library with books (eigenvalues) and successful book clubs (eigenvectors) formed only if there’s enough interest. If each book gets a corresponding book club with sufficient members to fully represent all ideas, the library is successfully organized (diagonalizable).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Algebraic Multiplicity: Refers to the number of times an eigenvalue appears in the characteristic polynomial.
-
Geometric Multiplicity: The dimension of the eigenspace corresponding to an eigenvalue, representing the number of linearly independent eigenvectors.
-
Diagonalizable Matrix: A matrix that can be represented as a product of eigenvectors and a diagonal matrix of eigenvalues.
-
Relationship: The inequality 1 ≤ GM(λ) ≤ AM(λ) indicates that GM is always less than or equal to AM.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
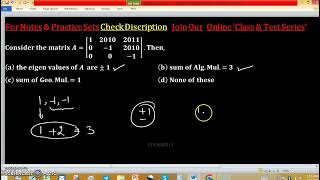
If the eigenvalue λ=4 has an algebraic multiplicity of 2, it means it appears twice in the characteristic polynomial, while if its geometric multiplicity is 1, there is only one linearly independent eigenvector.
-
For a matrix with two eigenvalues, λ1=3 (AM=1, GM=1) and λ2=1 (AM=1, GM=0), the matrix is diagonalizable as the GM equals AM for both eigenvalues.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Count your roots, don’t let them stray, AM helps in a major way.
📖 Fascinating Stories
-
Imagine a city where each house represents an eigenvalue. The algebraic multiplicity is how many doors each house has, while geometric multiplicity is how many paths lead out of that house!
🧠 Other Memory Gems
-
Remember 'Geometric Gives Dimension' for geometric multiplicity.
🎯 Super Acronyms
Use 'AGD' to remember Algebraic, Geometric, and Dimension.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Algebraic Multiplicity
Definition:
The number of times an eigenvalue appears as a root of the characteristic polynomial.
-
Term: Geometric Multiplicity
Definition:
The dimension of the eigenspace corresponding to an eigenvalue; the number of linearly independent eigenvectors for that eigenvalue.
-
Term: Eigenspace
Definition:
The set of eigenvectors corresponding to an eigenvalue, along with the zero vector.
-
Term: Diagonalizable Matrix
Definition:
A matrix that can be expressed in the form A=PDP⁻¹, where D is a diagonal matrix.