Eigenvectors and Eigenspaces
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Eigenvectors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will dive into the world of eigenvectors. An eigenvector is a non-zero vector that changes only by a scalar factor when a linear transformation is applied to it. Can anyone explain what that means in simpler terms?

Does that mean they point in the same direction even if they get longer or shorter?

Exactly, Student_1! That's a great way to think about it. If we have a matrix **A** and an eigenvector **v**, when we multiply them, we get a scaled version of **v**: **Av = λv**. Who can tell me what **λ** represents?

It's the eigenvalue, right?

Correct! Now, can anyone summarize how we go about finding the eigenvectors of a matrix?

We solve the equation by finding the characteristic polynomial and then finding the null space of **A - λI**.

Well done, Student_3! Finding the characteristic polynomial is the first step.
Eigenspaces and Their Properties
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's shift our focus to eigenspaces. The eigenspace corresponding to an eigenvalue **λ** is defined as the set of all eigenvectors that satisfy **Av = λv**. How can we express this mathematically?

We can say **E = Null(A - λI)**, right?

Spot on! And why is the concept of null space essential in understanding eigenspaces?

It shows that eigenspaces are subspaces of **Rⁿ**, which helps in understanding their structure.

Exactly, Student_4! Now, we also talk about geometric and algebraic multiplicities. Who can explain these concepts?

Geometric multiplicity is the dimension of the eigenspace, while algebraic multiplicity is how many times the eigenvalue is a root of the characteristic polynomial.

Excellent! The relation between these two multiplicities is crucial for understanding whether a matrix can be diagonalizable.
Applications of Eigenvectors in Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've discussed the theory, let’s look at how eigenvectors apply in real-world civil engineering scenarios. How do you think understanding eigenvalues and eigenvectors would help engineers?

It could help in analyzing structures, like when looking for natural frequencies in buildings.

Exactly! If we know the eigenvectors, we can identify mode shapes. This information is crucial in designing buildings to withstand seismic forces. Can anyone think of other applications?

What about stress-strain analysis? Eigenvectors could help in finding principal stresses.

Great example, Student_2! Recognizing the orientations of principal stresses through eigenvalues allows for better material selection and design. Remember the phrase 'Eigenvalues help engineers evaluate' to recall this idea!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section explains the definitions of eigenvectors and eigenspaces. It covers how to determine eigenvalues, find eigenspaces, and the significance of geometric and algebraic multiplicities. The role of these concepts in civil engineering applications is also highlighted.
Detailed
Eigenvectors and Eigenspaces
In linear algebra, eigenvectors and eigenvalues play a crucial role in understanding matrix behavior. Given an n×n matrix A, a non-zero vector v is an eigenvector corresponding to a scalar λ (eigenvalue) if it satisfies the equation Av = λv. The collection of all eigenvectors corresponding to a specific eigenvalue forms the eigenspace, denoted as E = {v ∈ Rⁿ : Av = λv}. This eigenspace can also be expressed as E = Null(A - λI), indicating a subspace of Rⁿ. The key metric associated with this eigenspace is its dimension, termed the geometric multiplicity of λ, which reveals how many linearly independent eigenvectors exist for a given eigenvalue. Understanding these concepts is essential for applications in civil engineering, such as structural analysis, where eigenvectors may represent fundamental modes of vibration or other critical system behaviors.
Youtube Videos






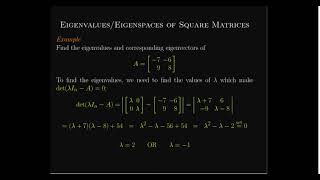


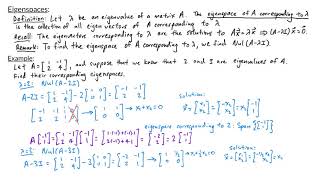
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Eigenvectors and Eigenvalues
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let A be an n×n matrix. If there exists a non-zero vector v∈Rn and a scalar λ∈R such that:
Av=λv
then λ is an eigenvalue of A, and v is an eigenvector corresponding to λ.
Detailed Explanation
In this chunk, we define the key concepts of eigenvalues and eigenvectors. We start with a square matrix A (which has the same number of rows and columns). If there is a non-zero vector v (this means it is not the zero vector) such that when we multiply matrix A by this vector, the output is simply a scaled version of the original vector v (scaled by λ), then λ is called an eigenvalue of matrix A, and v is the corresponding eigenvector. This relationship means that the action of matrix A on vector v does not change the direction of v; it only changes its magnitude (by scaling).
Examples & Analogies
Think of eigenvectors as the 'main directions' in which forces act within a building during stress analysis. Just like a gust of wind pushing against a building can cause it to sway in certain predictable directions (eigenvectors), eigenvalues help us determine how strong that sway will be (how much it stretches or shrinks).
Understanding Eigenspace
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The eigenspace corresponding to an eigenvalue λ is the set:
E = {v∈Rn:Av=λv}
It can also be expressed as:
E = Null(A−λI) which is a subspace of Rn. The dimension of Eλ is called the geometric multiplicity of λ.
Detailed Explanation
This chunk discusses the concept of eigenspace, which is the collection of all eigenvectors that share the same eigenvalue, along with the zero vector. Mathematically, the eigenspace for an eigenvalue λ of matrix A can be represented as all vectors v that satisfy the equation Av = λv. Another way to look at this is through the null space of the matrix (A − λI), where I is the identity matrix. This eigenspace is a vector subspace, meaning it is closed under addition and scalar multiplication. The geometric multiplicity of an eigenvalue λ refers to the number of linearly independent eigenvectors that can be found in this eigenspace.
Examples & Analogies
Think of the eigenspace as a multi-layered structure. Each eigenvalue corresponds to a different layer of the structure, with the eigenvectors being the individual paths of movement possible within that layer. If you picture a building, the eigenspace could represent all the possible ways it could sway (eigenvectors) for a certain strength of wind (eigenvalue) without shifting into a different structural form.
Key Concepts
-
Eigenvector: A vector that satisfies the equation Av = λv.
-
Eigenspace: A set of all eigenvectors corresponding to an eigenvalue.
-
Geometric Multiplicity: Dimension of the eigenspace corresponding to an eigenvalue.
-
Algebraic Multiplicity: The number of times an eigenvalue appears in the characteristic polynomial.
Examples & Applications
The matrix A = [[4, 1], [0, 4]] has an eigenvalue of 4 with algebraic multiplicity of 2 and geometric multiplicity of 1, indicating it is not diagonalizable.
In structural engineering, eigenvectors can represent mode shapes of vibrations in buildings subjected to seismic forces.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When you find a vector that stays the same, it's an eigenvector, that's its name!
Stories
Imagine a magic spell that stretches a rope. That rope is our eigenvector, transforming without changing direction—just like eigenvectors under matrix transformations.
Memory Tools
Use 'EGAL' to remember: Eigenspace, Geometric and Algebraic Multiplicity, and Linear independence!
Acronyms
EVA
Eigenvalues lead to Vectors that are Awesome! (Think about how eigenvalues relate to eigenvectors.)
Flash Cards
Glossary
- Eigenvector
A non-zero vector v such that Av = λv for some scalar λ.
- Eigenspace
The null space of the equation A - λI, representing a vector subspace associated with eigenvalue λ.
- Eigenvalue
A scalar λ associated with a matrix A, which indicates how much the eigenvector is stretched or compressed.
- Geometric Multiplicity
The dimension of the eigenspace associated with an eigenvalue.
- Algebraic Multiplicity
The number of times an eigenvalue appears as a root of the characteristic polynomial.
Reference links
Supplementary resources to enhance your learning experience.
