Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvectors and Eigenspaces
Unlock Audio Lesson
Today, we are diving into eigenvectors and eigenspaces. Can anyone tell me what an eigenvector is?
I think it's a special kind of vector connected to matrices.
Exactly! An eigenvector is a non-zero vector **v** that satisfies the equation **Av = λv**, where **λ** is known as the eigenvalue. The eigenspace associated with an eigenvalue **λ** consists of all eigenvectors corresponding to it. Can someone explain how we can express this mathematically?
Is it something like **E = Null(A - λI)**?
Perfect! This means the eigenspace is essentially the null space of **(A - λI)**, a subspace of **ℝⁿ**. Understanding this is important for later sections. So, what do you think the dimension of an eigenspace represents?
Is it the number of linearly independent eigenvectors?
Correct! That's what we call the geometric multiplicity of an eigenvalue. Great teamwork!
Finding Eigenvalues and Eigenspaces
Unlock Audio Lesson
Now, let’s talk about the steps to find the eigenvalues of a matrix. Can anyone remind us how to start?
We need to solve the characteristic equation, **det(A - λI) = 0**.
Exactly! Solving this equation gives us the eigenvalues. Once we have them, what’s our next step?
We solve **(A - λI)v = 0** for each eigenvalue to find the eigenspace.
Precisely! This gives us the null space for that specific eigenvalue. If we find the vectors that span this space, what do we get?
We get the basis of the eigenspace!
Correct! Remember, this basis consists of linearly independent eigenvectors. Let's see if we can find one for a matrix example in our next session.
Algebraic and Geometric Multiplicity
Unlock Audio Lesson
So, we’ve discussed finding bases for eigenspaces. Now, let’s dive into the concepts of algebraic and geometric multiplicity. Can anyone tell me what these terms mean?
Algebraic multiplicity is how many times an eigenvalue appears as a root in the characteristic polynomial.
And geometric multiplicity is the dimension of the eigenspace for that eigenvalue, right?
Yes! The key relationship here is **1 ≤ GM(λ) ≤ AM(λ)**. This tells us that the geometric multiplicity cannot exceed the algebraic multiplicity. What does it imply if they are equal?
It means the matrix is diagonalizable!
Very well summarised! Being able to diagonalize a matrix is crucial for simplifying computations involving it.
Practical Applications in Engineering
Unlock Audio Lesson
Finally, let’s look into how this knowledge applies to civil engineering. Can anyone think of an application for eigenvectors?
They are used in modal analysis to study vibrations of structures.
Exactly! Each mode shape corresponds to an eigenvector. How about the implications of eigenvectors in structural dynamics?
In seismic analysis, right? They help us understand how buildings will respond during earthquakes!
Yes! Eigenvalues represent natural frequencies, while eigenvectors tell us the mode shapes—critical for ensuring structures can withstand dynamic loads.
So, the ability to diagonalize matrices is connected to solving these problems effectively?
Absolutely! Well done, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we discuss the definitions and properties of eigenvectors and eigenspaces, their basis, and the methods for determining this basis, emphasizing their significance in engineering fields such as structural analysis and dynamics. The concepts of algebraic and geometric multiplicity are also introduced, along with practical applications and examples illustrating these ideas.
Detailed
Detailed Summary
In linear algebra, eigenvectors and their corresponding eigenvalues are critical for understanding matrix behavior, particularly for applications in civil engineering. This section provides foundational knowledge regarding eigenvectors, defining them as non-zero vectors that satisfy the equation Av = λv, where λ is called the eigenvalue. Each eigenvalue has an associated eigenspace, defined as the set of all eigenvectors corresponding to λ, which can be expressed as E = Null(A - λI), a subspace of ℝⁿ.
To find a basis for an eigenspace, students are guided through a structured process consisting of finding eigenvalues via the characteristic equation and solving the system (A - λI)v = 0 to identify the eigenspace. The basis consists of a set of linearly independent eigenvectors spanning this eigenspace, and understanding the relationship between algebraic and geometric multiplicity is crucial. Finally, engineering applications are highlighted, emphasizing the role of eigenvectors in structural analysis and modal dynamics, with an example illustrating the steps taken to derive eigenvectors from a specified matrix.
Youtube Videos
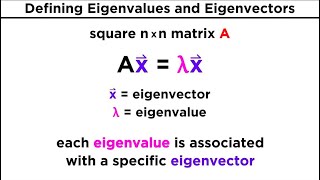
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Eigenvectors and Eigenspaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the study of linear algebra, especially for systems that arise in civil engineering—like structural analysis, fluid mechanics, or stress-strain problems—understanding eigenvalues and eigenvectors is essential. Once the eigenvectors of a matrix are determined, they can form a basis for vector spaces associated with the matrix, especially the eigenspaces. This chapter focuses on how eigenvectors form a basis, how to construct such bases, and the implications in engineering applications such as analyzing structural modes or vibrations.
Detailed Explanation
This chunk introduces the importance of eigenvectors in linear algebra, especially in engineering contexts. Eigenvectors are key to understanding how systems behave under various conditions, particularly in fields like civil engineering, where they help analyze structures and their responses to forces. The core idea is that eigenvectors can create a structured framework (basis) for understanding complex vector spaces.
Examples & Analogies
Consider a tall building during an earthquake. Just like how a tree sways in the wind, the building will have certain 'modes' of motion. These modes can be understood through its eigenvectors, which represent directions in which the building naturally vibrates. An architect can design the building to handle these vibrations effectively, ensuring safety.
Understanding Eigenspaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let A be an n×n matrix. If there exists a non-zero vector v∈Rn and a scalar λ∈R such that: Av=λv, then λ is an eigenvalue of A, and v is an eigenvector corresponding to λ. The eigenspace corresponding to an eigenvalue λ is the set: E ={v∈Rn:Av=λv}. It can also be expressed as: E =Null(A−λI) which is a subspace of Rn. The dimension of Eλ is called the geometric multiplicity of λ.
Detailed Explanation
Here we define what an eigenspace is. An eigenspace arises from an eigenvalue of a matrix and consists of all eigenvectors corresponding to that eigenvalue, along with the zero vector. It is important because it tells us how many directions (vectors) can be formed with respect to the eigenvalue. The dimension of this eigenspace, called geometric multiplicity, informs us how many linearly independent eigenvectors exist for a given eigenvalue.
Examples & Analogies
Think of a concert hall where sound can resonate in specific directions. Each direction in which sound is amplified corresponds to an eigenvector, while the eigenspace represents all possible ways in which sound can resonate within that hall based on its structure. The geometric multiplicity tells us how many such resonating modes exist.
Finding the Basis of an Eigenspace
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To understand the basis of eigenvectors, we focus on finding a basis for each eigenspace Eλ. Let’s suppose: • A is an n×n matrix • λ is an eigenvalue of A • We solve (A−λI)v=0. The solutions to this homogeneous system form a vector space, and the vectors that span this space are the eigenvectors corresponding to λ. A basis of the eigenspace is a linearly independent set of eigenvectors that spans the entire eigenspace.
Detailed Explanation
In this chunk, we focus on the method of finding a basis for an eigenspace. By solving the equation (A-λI)v=0, we determine the eigenvectors associated with an eigenvalue. The solution set reveals the structure of the eigenvectors, and a collection of those that are linearly independent forms the basis for that eigenspace. Understanding how to find this basis is crucial for further applications and calculations.
Examples & Analogies
Consider a music band where each musician plays a unique instrument. The entire group represents the 'eigenspace.' If we select a few musicians who can play together without outshining one another, we create a balanced ensemble. These selected musicians form the 'basis' for the band's sound, just as linearly independent eigenvectors form the basis of an eigenspace.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvector: A vector satisfying the equation Av = λv for some eigenvalue λ.
-
Eigenspace: The set of eigenvectors corresponding to a given eigenvalue, represented as E = Null(A - λI).
-
Algebraic Multiplicity: The count of a specific eigenvalue's occurrence in the characteristic polynomial.
-
Geometric Multiplicity: The number of independent eigenvectors associated with an eigenvalue.
-
Diagonalization: A process where a matrix is expressed in the form A = PDP^-1 where P contains eigenvectors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a basic 2x2 matrix and its eigenvalues/eigenvectors derived using the characteristic polynomial.
-
An application of eigenvectors in structural analysis for determining the mode shapes of a vibrating beam.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvectors dance in line, in eigenspaces they shine; with λ they align.
📖 Fascinating Stories
-
Imagine a town where each building stands tall. The eigenvectors are the structure's way of responding to a tremor—their unique shapes help the town's engineers understand how to reinforce them for safety.
🧠 Other Memory Gems
-
Remember EAGD: Eigenvectors, Algebraic multiplicity, Geometric multiplicity, Diagonalizable—it's a formula for understanding matrices.
🎯 Super Acronyms
Think of **EA-ME** for Eigenvalues and Multiplicities Explained.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvector
Definition:
A non-zero vector v that satisfies the equation Av = λv.
-
Term: Eigenvalue
Definition:
A scalar λ corresponding to an eigenvector such that Av = λv.
-
Term: Eigenspace
Definition:
The set of all eigenvectors corresponding to an eigenvalue, defined as E = Null(A - λI).
-
Term: Algebraic Multiplicity
Definition:
The number of times an eigenvalue appears as a root of the characteristic polynomial.
-
Term: Geometric Multiplicity
Definition:
The dimension of the eigenspace associated with an eigenvalue.
-
Term: Diagonalizable
Definition:
A matrix is diagonalizable if it has enough linearly independent eigenvectors to form a basis for ℝⁿ.