Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Complex Eigenvalues
Unlock Audio Lesson
Today, we're delving into complex eigenvalues. Can anyone recall what an eigenvalue refers to in the context of a matrix?
Isn't it a scalar for which there exists a non-zero vector that, when multiplied by the matrix, gives the same vector scaled by that scalar?
Exactly! Now, in some matrices, like our example matrix B we're using, the eigenvalues can be complex. In B, we find that the eigenvalues are ±i. Does anyone know why this might be significant?
Could it be because they represent oscillations in systems? Like, in engineering?
Correct! Complex eigenvalues often relate to oscillatory behavior, which is crucial in structural dynamics.
Finding Complex Eigenvectors
Unlock Audio Lesson
Now that we understand complex eigenvalues, let's explore how to find their corresponding eigenvectors. For example, how would we set up the equation for finding the eigenvector corresponding to ±i
We would set up the equation (B - λI)v = 0, right? But using i or -i as λ?
Yes, exactly! We substitute i for λ into our equation and solve for v. This could lead us to complex eigenvectors. Can someone summarize why we might prefer real representations?
Because in most engineering applications, we need real values to describe motions or oscillations, and Euler's formula helps convert complex forms into real ones!
Excellent summary!
Application of Complex Eigenvalues
Unlock Audio Lesson
Finally, let’s discuss the applications of complex eigenvalues. Why are they important in scenarios like structural dynamics?
They help in analyzing vibrations or oscillations in structures, particularly during events like earthquakes!
Exactly! We use complex solutions to describe how structures respond to dynamic loading. What tool do we often use to convert these into real-world applications?
Euler's Formula, which relates complex exponentials to sine and cosine functions!
Perfect! This conversion allows us to draw practical insights from complex eigenvalues.
Importance of Complex Eigenvalues in Engineering
Unlock Audio Lesson
Let's summarize how critical complex eigenvalues are in engineering applications. Can anyone explain why it’s essential to consider them?
Since they indicate oscillations, ignoring them might lead to underestimating forces a structure could experience!
Great point! Those oscillations could cause failure if not properly addressed in design. Any final thoughts?
Understanding them really seems important for safe engineering practices!
Absolutely! Today’s learning about complex eigenvalues equips you to appreciate how mathematics applies to real-world challenges.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore complex eigenvalues that arise in certain real matrices. We discuss how complex eigenvectors are found, and the implications of complex eigenvalues in engineering contexts, particularly in interpreting oscillatory behavior using trigonometric functions derived from Euler's formula.
Detailed
Complex Eigenvalues and Basis
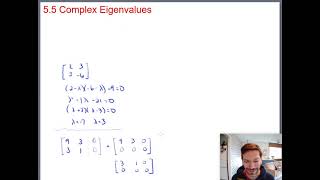
In linear algebra, particularly when dealing with matrices, it is essential to understand that eigenvalues can sometimes be complex numbers. This section focuses specifically on matrices that exhibit complex eigenvalues. For instance, consider the matrix:
B = | 0 -1 |
| 1 0 |
The characteristic polynomial of this matrix reveals that it has complex eigenvalues, which can be expressed as i and -1. As we derive complex eigenvectors corresponding to these eigenvalues, it is important to note that these vectors do not span a basis over
\[ \mathbb{R}^n \]
but rather over
\[ \mathbb{C}^n \].
This is critical in applications such as engineering, where scenarios like oscillations and vibrations require interpretation of complex eigenvalues. Such interpretations often utilize Euler's formula, which links complex exponentials to trigonometric functions, thereby enabling the conversion of complex solutions into real-valued outcomes during analysis.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Complex Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In some real matrices, eigenvalues may be complex. For example:
B =
[0 -1]
[1 0]
Characteristic polynomial:
det(B−λI)=λ² + 1 = 0 ⇒ λ = ±i
Detailed Explanation
This chunk introduces the concept that not all eigenvalues of a matrix are real numbers. In particular, the matrix B is presented. When we calculate its characteristic polynomial, we find that it results in a quadratic equation, yielding complex solutions ±i, which are imaginary numbers. This occurs in certain cases of real matrices, indicating that the matrix does not behave traditionally as expected.
Examples & Analogies
Think of riding a swing. Usually, you move back and forth in one direction (a real movement). However, imagine if the swing allowed you to twist around as well, creating a swirling motion (like complex eigenvalues). Just like some motions can be described with regular directions, others, particularly oscillations, might require additional dimensions (the complex numbers) to describe the behavior effectively.
Complex Eigenvectors and Their Basis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For complex eigenvalues, we find complex eigenvectors. However, these may not form a basis over Rn, only over Cn.
Detailed Explanation
This chunk explains that when eigenvalues are complex, the associated eigenvectors are also complex. While these complex eigenvectors can span a vector space, they do not form a basis over the real numbers (Rn), but they can form a basis over the complex numbers (Cn). This distinction is important because it determines how we can use these vectors in practical applications, particularly those that require real number solutions.
Examples & Analogies
Imagine a colorful garden where different colors of flowers represent different properties of a system. If you only look at the colors (real numbers), you miss out on the delightful fragrances and combinations (complex numbers). The complex eigenvectors give a fuller, richer understanding of the underlying mathematics, much like how fragrances add depth to the visual experience of a garden.
Applications of Complex Eigenvalues in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In engineering applications (e.g., oscillations), these are interpreted using Euler’s formula to convert to real-valued trigonometric solutions.
Detailed Explanation
This chunk discusses how complex eigenvalues and eigenvectors have practical applications in engineering, especially in the context of oscillatory systems. Engineers often use Euler's formula to represent complex exponential functions in terms of sine and cosine functions—this allows them to derive all real solutions for physical systems such as vibrations, electrical circuits, and mechanical systems. These trigonometric solutions help make sense of oscillations in real-world applications.
Examples & Analogies
Consider the water ripples created when a stone is thrown into a pond. The ripples are oscillatory and can be described mathematically using real functions (like sine and cosine). Even if the underlying mathematical model uses complex numbers, you can visualize the ripples as a physical phenomenon that translates those complex solutions into real-life behavior.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Complex Eigenvalues: Eigenvalues that are not real, often resulting from certain matrix forms.
-
Eigenvectors Correspondence: Complex eigenvectors may not form a real basis but can be interpreted using trigonometric identities.
-
Importance in Engineering: Complex eigenvalues are crucial for understanding dynamic systems, particularly in modeling oscillations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For B = [[0, -1], [1, 0]], the characteristic polynomial shows eigenvalues ±i, indicating oscillatory solutions.
-
In engineering, a system with complex eigenvalues might describe the dynamic behavior of structures under loading, highlighting importance in design.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In matrices that rotate or spin, Complex eigenvalues help us win
📖 Fascinating Stories
-
Imagine a structure that sways to a rhythm, its oscillations are modeled by complex eigenvalues, dancing in harmony.
🧠 Other Memory Gems
-
C-E (Complex - Eigenvalue): C for Complex, E for Eigenvalue, helping remember they can exist in pairs.
🎯 Super Acronyms
COPS
- Complex Eigenvalues in Oscillatory Problems in Structures.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Complex Eigenvalue
Definition:
An eigenvalue that takes on complex numbers, arising in certain matrices.
-
Term: Eigenvector
Definition:
A non-zero vector that, when multiplied by a matrix, yields a scalar multiple of itself.
-
Term: Euler's Formula
Definition:
A formula that establishes the relationship between complex exponentials and trigonometric functions.