Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Diagonalization
Unlock Audio Lesson
Today, we are discussing diagonalization. What do you all know about this concept?
I think diagonalization is about transforming a matrix into a diagonal form.
That's correct! Diagonalization occurs when we can express a matrix A in the form A = PDP⁻¹, where P contains eigenvectors, and D contains eigenvalues. Why do you think this is important?
It helps simplify calculations with matrices, right?
Exactly! When we diagonalize a matrix, operations like raising the matrix to a power become much easier.
Eigenvectors and Diagonalization
Unlock Audio Lesson
To diagonalize a matrix, we need n linearly independent eigenvectors. Can anyone explain what that means?
Does it mean we need a full set of eigenvectors for every dimension of the matrix?
Correct! For an n×n matrix, we need n eigenvectors that are not scalar multiples of each other. If any eigenvalue has a geometric multiplicity less than its algebraic multiplicity, the matrix cannot be diagonalized.
So, if we have too few unique eigenvectors, we can't simplify the matrix?
Exactly! Understanding the eigenvector basis helps in recognizing whether diagonalization is possible.
Importance of Diagonalization in Applications
Unlock Audio Lesson
Let's talk about where diagonalization is applied, particularly in civil engineering.
Modal analysis, right? It simplifies vibration and structural analysis.
Correct! Eigenvectors represent mode shapes, which are crucial for understanding system stability. How does diagonalization help in these applications?
It reduces complex systems into simpler components we can analyze!
Exactly! This makes predictions and engineering decisions much easier.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses how a matrix can be diagonalized if it has n linearly independent eigenvectors, forming a complete basis for Rⁿ. The diagonalization process A=PDP⁻¹ is detailed, highlighting the definitions and importance of the matrix P and the diagonal matrix D. Understanding these concepts is critical for applications in civil engineering and other fields.
Detailed
Diagonalization and Basis of Eigenvectors
In linear algebra, the process of diagonalization involves expressing a matrix A in the form:
$$
A = PDP^{-1}
$$
where:
- P is a matrix composed of the eigenvectors of A. Each column of P represents a linearly independent eigenvector, creating a basis for the vector space Rⁿ.
- D is a diagonal matrix containing the corresponding eigenvalues associated with each eigenvector in P.
Diagonalization is feasible only if the matrix possesses n linearly independent eigenvectors, hence forming a complete basis for Rⁿ. This property is crucial for simplifying many mathematical computations, especially in applications such as structural analysis in civil engineering where understanding the matrix's behavior under transformations is essential.
Youtube Videos
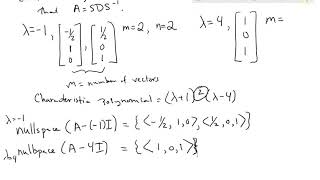
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Diagonalization Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If a matrix A has n linearly independent eigenvectors, then:
A = PDP^−1
Where:
- P is a matrix with columns as eigenvectors (a basis of eigenvectors),
- D is a diagonal matrix with corresponding eigenvalues.
Detailed Explanation
This chunk introduces the concept of diagonalization of a matrix. Diagonalization occurs when a square matrix can be expressed in the form A = PDP^−1, where:
- A is the original matrix.
- P is an arranged matrix where each column consists of linearly independent eigenvectors of A. This means that the eigenvectors can be used as a basis for the vector space associated with A.
- D is a diagonal matrix whose diagonal elements are the eigenvalues corresponding to the eigenvectors in P. Diagonal matrices are preferred as they simplify many matrix operations, such as raising a matrix to a power or solving systems of linear equations.
For this diagonalization to be feasible, it is essential that there are enough linearly independent eigenvectors to span the whole space, which requires A to have as many linearly independent eigenvectors as the dimension of the matrix (n in this case).
Examples & Analogies
Imagine a complex stereo system with various channels for sound. Each channel can be thought of as an eigenvector. If each channel functions independently, you can easily adjust the sound and balance effectively. But if one channel is missing, you can't use the stereo at its full potential. Similarly, diagonalization allows us to break down complex matrices into simpler and more manageable parts through their eigenvectors, just as a complete set of stereo channels helps create the best sound.
Conditions for Diagonalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is diagonalization, and it's only possible if eigenvectors form a complete basis for Rn.
Detailed Explanation
The chunk emphasizes a crucial condition for diagonalization: a square matrix can only be diagonalized if its eigenvectors form a complete basis for the vector space Rn. This means that
- The number of linearly independent eigenvectors must equal the dimension of the space (n). If a matrix does not meet this criterion, it cannot be diagonalized. This property is particularly important in applications, as diagonal matrices allow for straightforward computations, whereas non-diagonalizable matrices complicate analysis.
Examples & Analogies
Think of a puzzle that consists of n pieces. To complete the picture, all pieces must fit together correctly. If you miss even one piece, the puzzle remains incomplete and cannot be displayed as intended. Similarly, for a matrix to be diagonalizable, it needs all its eigenvectors (analogous to puzzle pieces) to be present and independent to fully represent the space.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Diagonalization: The process of expressing a matrix as A=PDP⁻¹.
-
Eigenvectors: Non-zero vectors that satisfy Av=λv.
-
Matrix P: A matrix formed from eigenvectors.
-
Matrix D: A diagonal matrix of corresponding eigenvalues.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Given a matrix with distinct eigenvalues, diagonalization can simplify calculations in engineering contexts.
-
Diagonalization is used in modal analysis to determine structural response to dynamic loads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To diagonalize, we align, Eigenvalues tell us how to define.
📖 Fascinating Stories
-
Imagine a group of friends (eigenvectors) gathered to help their friend A ($$A=PDP^{-1}$$) reach a simple destination (diagonal form). Each friend contributes uniquely, ensuring they can all fit in one vehicle (the diagonal matrix).
🧠 Other Memory Gems
-
P for People, D for Directions – think of eigenvectors guiding matrix A to diagonalization.
🎯 Super Acronyms
PDE = P for eigenvectors, D for diagonal values, and E for Eigen — remember to diagonalize!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Diagonalization
Definition:
The process of converting a matrix into a diagonal form via a similarity transformation.
-
Term: Eigenvector
Definition:
A non-zero vector v such that Av=λv, where A is a matrix and λ is a scalar.
-
Term: Matrix P
Definition:
A matrix whose columns are linearly independent eigenvectors of A.
-
Term: Matrix D
Definition:
A diagonal matrix consisting of the eigenvalues corresponding to the eigenvectors in matrix P.