Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvectors in Structural Dynamics
Unlock Audio Lesson
Today, we’ll explore how eigenvectors are crucial in understanding structural dynamics. Can anyone tell me why we might need to analyze vibrations in structures?
I think it's to ensure that buildings can withstand forces like earthquakes or strong winds.
Exactly! Eigenvectors help us understand the different ways a structure vibrates. The equation Kx = λMx captures this relationship. Does anyone know what K and M represent?
K is the stiffness matrix, and M is the mass matrix.
Correct! In our context, λ represents the square of the natural frequencies. Can anyone recall what mode shapes correspond to?
They correspond to the eigenvectors of the system.
Right! Orthogonality of these eigenvectors also simplifies our analyses. Each mode shape behaves independently. Why do you think that's important?
It makes it easier to study complex systems by breaking them down.
Great answer! In summary, understanding eigenvectors through this lens allows engineers to build safer, more resilient structures.
Generalized Eigenvalue Problem
Unlock Audio Lesson
Let’s dive deeper into the eigenvalue problem. Remember that from the stiffness and mass matrices, we get the equation Kx = λMx. What is this equation commonly referred to?
The generalized eigenvalue problem!
Correct! How does this form help us in modal analysis?
It allows us to find the mode shapes and frequencies of a structure.
Exactly! Each solution gives us an eigenvalue, which translates into frequencies. Can you think of an application where understanding these frequencies would be crucial in engineering?
In designing buildings in earthquake-prone areas!
Great example. Engineers must ensure that structures don’t resonate with seismic waves. To conclude this session, remember: the eigenvalue problem simplifies complex dynamics into actionable insights.
Decoupling Systems using Modal Analysis
Unlock Audio Lesson
Now, let’s consider how eigenvectors allow us to decouple systems into independent SDOF systems. Can someone explain why decoupling is beneficial?
It helps simplify the analysis by focusing on one vibration mode at a time.
Exactly! By addressing each mode separately, we can greatly reduce the mathematical complexity involved. What would be a practical outcome of decoupling?
It allows for targeted reinforcement of weak modes in a building.
Exactly right! Each mode can be analyzed independently. This modularity aids in both design and safety assessments. Can anyone recap how orthogonality of eigenvectors contributes to this?
Orthogonal eigenvectors mean that there's no interference between vibration modes, making each analysis straightforward.
Perfectly summarized. In practice, this leads to more effective engineering solutions tailored to specific dynamic responses.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
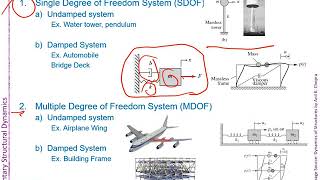
In structural dynamics, eigenvectors and eigenvalues are fundamental in understanding the behavior of structures under dynamic loads. They define mode shapes and natural frequencies, enabling engineers to simplify complex systems into manageable forms for analysis, notably in modal analysis and stability evaluations.
Detailed
Role in Structural Dynamics
In civil engineering, particularly in the context of structural dynamics and vibrations, eigenvectors play a pivotal role. They arise from the generalized eigenvalue problem defined by the stiffness matrix (K) and mass matrix (M) established in the equation:
Kx = λMx,
where λ represents the square of the natural frequencies (ω²), and x indicates the mode shapes (which correspond to the eigenvectors). These mode shapes illustrate the independent directions in which a structure can vibrate.
Key Properties:
- Eigenvectors, interpreted as mode shapes, are orthogonal with respect to either the mass or stiffness metric, enabling beneficial analytical methodologies.
- This orthogonality is particularly advantageous in modal analysis, allowing the system to be decoupled into independent Single Degree of Freedom (SDOF) systems, facilitating simpler dynamic analysis of complex structures.
Overall, an understanding of eigenvectors and their computation is essential for effective structural design, particularly in areas susceptible to dynamic loads such as seismic activity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Generalized Eigenvalue Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In civil engineering, particularly in structural dynamics and vibrations, the stiffness matrix K and mass matrix M define the equation:
K x=λMx
This is a generalized eigenvalue problem.
Detailed Explanation
This chunk discusses a fundamental equation used in structural dynamics known as the generalized eigenvalue problem. In this equation, 'K' represents the stiffness matrix of the structure, while 'M' denotes the mass matrix. The vector 'x' is what we call the mode shapes (eigenvectors) of the system. The scalar 'λ' represents the squares of the natural frequencies of the system. Essentially, this equation helps engineers understand how structures will respond under dynamic loads, such as during an earthquake or when subjected to vibrations.
Examples & Analogies
Imagine a suspension bridge swaying gently in the wind. The stiffness matrix 'K' represents how rigid the bridge is, while the mass matrix 'M' indicates how much weight the bridge carries. The equation Kx = λMx allows engineers to predict how the bridge will move and respond to various forces, much like how a musician controls the pitch of a violin string through tension.
Mode Shapes as Independent Directions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• λ: Square of natural frequencies ω²
• x: Mode shapes (eigenvectors)
These mode shapes form a basis of independent vibration directions.
Detailed Explanation
Here, we explore what mode shapes and natural frequencies represent in structural dynamics. The square of the natural frequency (λ) is crucial for understanding how a structure will resonate when exposed to dynamic forces. The vectors 'x' denote the mode shapes, which signify the various ways a structure can vibrate independently. When engineers analyze these mode shapes, they can effectively design structures to withstand dynamic loads by ensuring that the frequencies do not match hazardous vibrations.
Examples & Analogies
Think about a children's swing set. When someone pushes a swing at just the right moment (synchronized with the swing's natural frequency), it goes higher. Each swing position represents a mode shape. To keep the swing stable, engineers must ensure that no one else pushes it at the same frequency, just like ensuring that a building does not sway at the same frequency as an earthquake.
Orthogonality of Mode Shapes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Eigenvectors (mode shapes) are orthogonal under the mass or stiffness metric.
Detailed Explanation
This chunk emphasizes an important property of the mode shapes, which is their orthogonality concerning the mass and stiffness matrices. Orthogonality means that the mode shapes are independent of one another; they do not interfere with each other when the structure vibrates. This characteristic allows engineers to analyze each mode independently, making calculations and simulations much more manageable.
Examples & Analogies
Imagine a piano where pressing one key (mode shape) does not affect other keys being pressed at the same time. Each key produces a distinct sound without interfering with the others, similar to how orthogonal mode shapes allow for clear, independent vibration behaviors in a structure.
Usage in Modal Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Used in modal analysis to decouple the system into independent SDOF (single degree of freedom) systems.
Detailed Explanation
In this chunk, we look at how the orthogonal mode shapes are utilized in modal analysis. By using these independent vibration modes, engineers can simplify complex dynamics into single degree of freedom (SDOF) systems. This approximation allows for easier analysis and design of structures, making it feasible to predict how a structure will behave under different loads without considering the entire complexity at once.
Examples & Analogies
Think about assembling a complicated Lego structure. Instead of figuring out how every piece interacts with every other piece at once, it’s easier to look at sections independently. By analyzing one section (SDOF) at a time, you can ensure that each functions correctly before seeing how they fit together in the final structure.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvectors are essential in analyzing vibrations and structural dynamics.
-
The generalized eigenvalue problem simplifies system analysis into independent mode shapes.
-
Understanding natural frequencies is crucial for ensuring structural safety under dynamic loads.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In analyzing a building subject to an earthquake, engineers use eigenvectors to determine how the structure will behave under seismic forces, identifying potential weak spots.
-
A bridge's stability is assessed by calculating its mode shapes, derived from eigenvalues and eigenvectors, to ensure it can endure dynamic loading.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To understand how buildings sway, Eigenvectors lead the way. They show us where to strengthen beams, In every way that structure dreams.
📖 Fascinating Stories
-
Imagine an old bridge that sways in the wind. Engineers used eigenvectors to find out how it moves, discovering ways to strengthen its foundation, ensuring it stands through any storm.
🧠 Other Memory Gems
-
To remember Kx = λMx: 'Keep eXploring Laminar Movements!'
🎯 Super Acronyms
SIMPLE
- Stiffness
- Independent Modes for Perceptible Loads & Energies.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvector
Definition:
A non-zero vector that satisfies the equation Av = λv, indicating a mode of behavior in a system.
-
Term: Eigenspace
Definition:
The set of all eigenvectors corresponding to a particular eigenvalue together with the zero vector.
-
Term: Generalized Eigenvalue Problem
Definition:
The mathematical problem involving the determination of eigenvalues and eigenvectors from the stiffness and mass matrices in structural dynamics.
-
Term: Mode Shape
Definition:
The shape that a structure takes during vibration at a particular frequency, represented by eigenvectors.
-
Term: Natural Frequency
Definition:
The frequency at which a system tends to oscillate in the absence of any driving force.