Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Eigenvalues
Unlock Audio Lesson
Today, we're discussing the significance of eigenvalues in determining the basis of an eigenspace. Can anyone tell me what an eigenvalue is?
Is it the value λ from the equation Av = λv?
Exactly! The eigenvalue λ relates to a specific vector Earth that isn’t altered in direction by the transformation represented by matrix A. It lengthens or shortens that vector.
So if we find the eigenvectors, we can understand how the matrix transforms space?
Exactly right! The eigenvectors associated with λ form a basis that can describe the entire eigenspace.
What does it mean for a set to be linearly independent?
Good question! Linear independence means no vector in the set can be expressed as a combination of the others. This is crucial for spanning the eigenspace.
Can we summarize what eigenvalues and eigenvectors do?
Sure! Remember, 'Eigenvalues are the lengths, and eigenvectors are the directions!'
Finding Eigenspaces
Unlock Audio Lesson
Now let's move on to finding eigenspaces. After identifying eigenvalues, what do we do next?
We need to solve the equation (A−λI)v = 0, right?
Correct! Solving this homogeneous equation will give us the null space, which is our eigenspace associated with eigenvalue λ.
And the solutions we find will be the eigenvectors?
Absolutely! The solutions form a vector space. To find the basis of this space, we need to ensure these vectors are linearly independent.
How do we check if they're linearly independent?
We can look for whether one vector can be expressed as a combination of the others, or use techniques like row-reduction on the corresponding matrix.
That sounds like a lot of work!
It can be, but it's crucial! Let's remember the acronym 'B.E.C' — Basis, Eigenvectors, Check!
Applications in Engineering
Unlock Audio Lesson
Finally, how do these concepts apply in civil engineering?
In modal analysis, eigenvectors represent different vibration modes of a structure.
Exactly! And understanding these modes helps engineers design structures that can withstand various stresses.
What about when the system is subject to seismic waves?
Great point! By analyzing eigenspaces, engineers can predict how buildings will respond during earthquakes.
So having a basis of eigenvectors is crucial for safety and stability?
That’s correct! Without a proper foundation in these concepts, engineers could encounter significant risks.
This really emphasizes the importance of linear algebra!
Absolutely! 'Understanding the basics leads to structural stability!' Let’s keep that in mind.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The basis of an eigenspace is a set of eigenvectors that spans the space and is linearly independent. This section explains the method to find the basis by first finding eigenvalues, then solving for the eigenspace, and finally ensuring the eigenvectors are sufficient to span the eigenspace. This process is essential for applications in engineering, particularly in the analysis of vibrations and stability.
Detailed
In linear algebra, understanding the basis of eigenspaces associated with eigenvalues is vital, especially in engineering applications. An eigenspace corresponding to an eigenvalue λ of a matrix A is defined as the set of eigenvectors that satisfy Av = λv, along with the zero vector. This section outlines the steps to find a basis for the eigenspace: firstly, compute the eigenvalues by solving the characteristic equation det(A−λI) = 0; secondly, identify the eigenspace by solving the homogeneous system (A−λI)v = 0; and lastly, extract a linearly independent set of eigenvectors from this solution set. The basis formed by these eigenvectors is crucial in various engineering fields such as structural dynamics, where understanding modes of vibrations enhances designs.
Youtube Videos
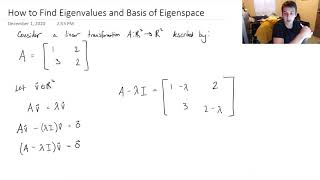
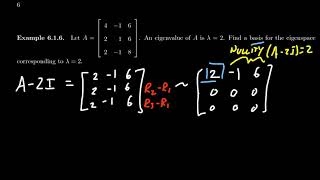
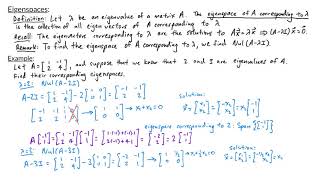
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Basis of Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To understand the basis of eigenvectors, we focus on finding a basis for each eigenspace \(E_\lambda\).
Let’s suppose:
- A is an n×n matrix
- \(\lambda\) is an eigenvalue of A
- We solve \((A−\lambda I)v=0\)
Detailed Explanation
This chunk introduces the concept of finding a basis of eigenvectors for a given eigenvalue \(\lambda\). First, we determine what it means to have a basis: it is a set of vectors that spans the vector space formed by the eigenspace corresponding to \(\lambda\). To find eigenvectors, we start with the matrix \(A\) and the eigenvalue \(\lambda\) and solve the equation \((A−\lambda I)v=0\), where \(I\) is the identity matrix. This equation is a homogeneous system of linear equations, and its solutions will give us the eigenvectors that form our basis.
Examples & Analogies
Imagine you are teaching a music class and want to teach a particular song. The notes you choose to play are analogous to the eigenvectors, while the full song represents the eigenspace. The eigenvectors must be unique but together create the complete music piece—this is the basis of your song.
Solutions Form a Vector Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The solutions to this homogeneous system form a vector space, and the vectors that span this space are the eigenvectors corresponding to \(\lambda\).
Detailed Explanation
When we solve the equation \((A−\lambda I)v=0\), the collection of solutions (eigenvectors) we find constitutes a vector space—specifically the eigenspace for that eigenvalue \(\lambda\). This means that any linear combination of these eigenvectors will also be in this vector space, thereby fulfilling one of the necessary conditions for a valid vector space: closure under addition and scalar multiplication.
Examples & Analogies
Think about filling a jar with water. Each drop of water represents an eigenvector. When combined, they fill the jar (the vector space). Just like you can mix and match drops to fill the jar to various levels, eigenvectors can be linearly combined to produce any vector in the eigenspace.
Basis of the Eigenspace
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A basis of the eigenspace is a linearly independent set of eigenvectors that spans the entire eigenspace.
Detailed Explanation
Once we find the eigenvectors corresponding to the eigenvalue \(\lambda\), we need to check if they form a basis. A basis must not only span the entirety of the eigenspace but must also consist of linearly independent vectors. This means no vector in the basis can be expressed as a linear combination of the others. If the eigenvectors satisfy these criteria, they collectively provide a complete way to construct any vector within that eigenspace.
Examples & Analogies
Consider a set of colored pencils. If every pencil (eigenvector) represents a unique color, then together they can create any color you want (span the eigenspace) as long as no two pencils are the same color (linearly independent). This way, you have a full palette to work with!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalues: Scalars that indicate how eigenvectors are stretched or compressed by a matrix.
-
Eigenvectors: Non-zero vectors that remain in the same direction under the transformation applied by the matrix.
-
Eigenspace: The vector space spanned by eigenvectors corresponding to a specific eigenvalue.
-
Basis of an Eigenspace: A linearly independent set of eigenvectors that span the eigenspace.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a matrix A, if λ=5 is an eigenvalue, then every eigenvector v satisfying Av=5v lies in the eigenspace for λ=5.
-
If a 2x2 matrix has eigenvalues of 2 and 3, we can find corresponding eigenvectors to define bases for the respective eigenspaces.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalues stretch, eigenvectors stay, in their space they dance and play.
📖 Fascinating Stories
-
Imagine a sailboat, the sail (eigenvector) catching the wind (eigenvalue) perfectly, guiding it across the sea without changing its direction—this illustrates the relationship in a matrix transformation.
🧠 Other Memory Gems
-
Remember 'V.E.A.' for eigenvectors, eigenvalues and eigenspaces.
🎯 Super Acronyms
Use 'B.E.C.' to remember
- Basis
- Eigenvectors
- Check for linear independence!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar λ such that Av = λv for a non-zero vector v.
-
Term: Eigenvector
Definition:
A non-zero vector v that satisfies Av = λv.
-
Term: Eigenspace
Definition:
The set of all eigenvectors corresponding to a particular eigenvalue, along with the zero vector.
-
Term: Basis of an Eigenspace
Definition:
A linearly independent set of eigenvectors that spans the eigenspace.
-
Term: Linear Independence
Definition:
A condition where no vector can be written as a linear combination of others in a set.