Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Diagonalizability
Unlock Audio Lesson
Let's discuss what it means for a matrix to be diagonalizable. Essentially, a matrix A is diagonalizable if we can represent it as A = PDP⁻¹, where P contains its eigenvectors and D is a diagonal matrix of eigenvalues.
What does it mean for a matrix to have n linearly independent eigenvectors?
Good question! It means that the eigenvectors span the entire space. For a matrix of size n, having n linearly independent eigenvectors indicates that we can express any vector in that space using these eigenvectors.
So if a matrix has fewer than n linearly independent eigenvectors, it can't be diagonalized?
Exactly! If any eigenvalue has geometric multiplicity less than its algebraic multiplicity, it’s a sign that the matrix won't be diagonalizable.
Are there any conditions under which a matrix is guaranteed to be diagonalizable?
Yes! If a matrix has n distinct eigenvalues, it is always diagonalizable. Symmetric matrices also have a nice property - they are guaranteed to be diagonalizable with orthogonal eigenvectors.
Wow, that makes diagonalization sound very important!
Absolutely! It is crucial in various applications, particularly in engineering for stability and modal analysis. Let's summarize these key concepts.
Diagonalization Formula
Unlock Audio Lesson
Now, let's focus on the diagonalization formula A = PDP⁻¹. Can anyone tell me what this means?
Is P just a matrix full of eigenvectors?
Exactly! The columns of P are the basis of eigenvectors corresponding to the eigenvalues in D. This relationship allows us to transform the matrix A into a simpler diagonal form. Anyone recall why this is useful?
It makes calculations easier, right? Like finding powers of the matrix?
That's spot on! By diagonalizing a matrix, you can easily compute its powers, eigenvalues, and more. Let’s conclude this section with the significance of diagonalizability in practical applications.
Applications in Engineering
Unlock Audio Lesson
Next, let’s talk about the real-world significance of diagonalization, especially in civil engineering.
How does diagonalization help in structural dynamics?
Great question! In structural dynamics, we work with the stiffness matrix K and mass matrix M. Diagonalization simplifies the analysis of these systems, allowing us to decouple them into simple systems.
So, diagonalization leads to a better understanding of vibrations and stability in structures?
Exactly! It helps engineers analyze how structures will respond to forces, including seismic activity. Before we wrap up, what have we learned today about diagonalizability?
We've learned it requires n linearly independent eigenvectors, and how to use the formula A = PDP⁻¹.
And its importance in applications like structural dynamics.
Excellent summary! Let’s move on to our glossary next.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section emphasizes the criteria for diagonalizability of a matrix, detailing how the existence of n linearly independent eigenvectors facilitates this process. It also discusses the implications of symmetric matrices being always diagonalizable and lays out the diagonalization formula.
Detailed
Diagonalizability and Basis of Eigenvectors
In linear algebra, specifically in the study of matrices and their properties, a matrix A is said to be diagonalizable if it can be expressed in the form:
A = PDP⁻¹, where P is a matrix composed of its eigenvectors and D is a diagonal matrix containing the eigenvalues of A.
For a matrix to achieve diagonalization, it must meet certain conditions:
- Linearly Independent Eigenvectors: A matrix A is diagonalizable if it possesses n linearly independent eigenvectors, where n is the dimension of the matrix. This means that every eigenvalue must have enough eigenvectors to form a basis.
- Distinct Eigenvalues: If a matrix has n distinct eigenvalues, it guarantees diagonalizability.
- Geometric and Algebraic Multiplicity: The geometric multiplicity (the number of linearly independent eigenvectors) should be equal to the algebraic multiplicity (the number of times an eigenvalue appears) for all eigenvalues. If any eigenvalue's geometric multiplicity is less than its algebraic multiplicity, the matrix cannot be diagonalized.
- Symmetric Matrices: Furthermore, symmetric matrices are always diagonalizable. This property stems from the fact that symmetric matrices possess real eigenvalues and orthogonal eigenvectors, making them ideal candidates for analysis in engineering applications, particularly in structural dynamics and vibrations.
Thus, understanding diagonalizability sheds light on the efficiency of analytical techniques used in engineering scenarios, such as stability analysis and modal analysis.
Youtube Videos
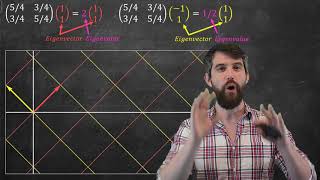
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Diagonalizability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Recall: A matrix A∈Rn×n is diagonalizable if and only if it has n linearly independent eigenvectors.
Detailed Explanation
A matrix is considered diagonalizable when it can be expressed in a specific form that simplifies various calculations. This means that the matrix has a sufficient number of unique directions (eigenvectors) that span its space. Specifically, to be diagonalizable, the matrix must have 'n' distinct directions where 'n' is the dimension of the space. If these directions are linearly independent, they can represent the transformations of the matrix efficiently.
Examples & Analogies
Think of diagonalizability like organizing books in a library. If you have a unique shelf for each book (or topic), it makes finding and categorizing them much easier. In contrast, if many books are stacked together without their unique shelves, it becomes complicated to sort them. The unique eigenvectors act like individual shelves that simplify the complex structure of the matrix.
Key Conditions for Diagonalizability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Key Conditions for Diagonalizability
- A has n distinct eigenvalues ⇒ Always diagonalizable.
- If any eigenvalue has geometric multiplicity < algebraic multiplicity, then A is not diagonalizable.
- Symmetric matrices are always diagonalizable with real eigenvalues and orthogonal eigenvectors.
Detailed Explanation
For a matrix to be diagonalizable, certain conditions must be met. First, if the matrix has 'n' distinct eigenvalues, it can be diagonalized without issue. Second, the relationship between geometric and algebraic multiplicity helps in determining diagonality. If the geometric multiplicity (the number of independent eigenvectors corresponding to an eigenvalue) is less than the algebraic multiplicity (the number of times that eigenvalue occurs as a root), then the matrix cannot be diagonalized. Lastly, symmetric matrices have special properties – they always have real eigenvalues and their eigenvectors can be arranged in a way that they are perpendicular to each other, which guarantees their diagonalizability.
Examples & Analogies
Imagine a team of players in a sport. If every player has a unique skill (distinct eigenvalues), the team is well-rounded and can play effectively (diagonalizable). However, if most players have overlapping skills (high algebraic multiplicity but low geometric multiplicity), the team lacks unique roles and might not function well together. Symmetric players, who possess a mix of skills and complement each other, represent symmetric matrices that are naturally well-balanced (diagonalizable).
Diagonalization Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Diagonalization Formula
A=PDP−1
- Columns of P: Basis of eigenvectors
- D: Diagonal matrix of eigenvalues
Detailed Explanation
The process of diagonalization can be mathematically represented by the equation A = PDP⁻¹, where A is the original matrix, P is a matrix made up of the eigenvectors, and D is a diagonal matrix containing the eigenvalues. The eigenvectors in P provide a new basis for the space, transforming the original matrix into a simpler form via D. This transformation makes it easier to perform calculations related to the matrix, as diagonal matrices are straightforward to work with when it comes to operations like exponentiation.
Examples & Analogies
Consider a complex route you need to travel in a big city with multiple roads and traffic signals. If you use a simple map (D), it's easy to navigate, but you need to know the starting point and how to get to the right intersection (P). The diagonalization process is like simplifying your journey by converting a complicated map into a straight path (the diagonal matrix), while keeping track of how to get there from any point (the eigenvectors). It streamlines your route for a clearer understanding of your travels.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Diagonalizable: Requires n linearly independent eigenvectors for a matrix to be expressed as A = PDP⁻¹.
-
Eigenvalues: These are the scalars associated with the eigenvectors and vital in the diagonalization process.
-
Algebraic and Geometric Multiplicity: AM reflects the count of eigenvalue occurrences, while GM indicates the number of independent eigenvectors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The characteristic polynomial of a matrix shows how the eigenvalues are determined, which is crucial for understanding diagonalizability.
-
Symmetric matrices being diagonalizable means they can be analyzed more easily due to their orthogonality.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To diagonalize with flair, eigenvectors must be rare; n must be the count so true, or matrix can't pass through.
📖 Fascinating Stories
-
Once upon a time in Matrix Land, there was a majestic square matrix who wished to transform into a diagonal shape. It sought out n distinct eigenvalues, gaining powerful eigenvectors that could transform it beautifully into the form A = PDP⁻¹.
🧠 Other Memory Gems
-
DIE - Diagonalizability Implies Eigenvalues.
🎯 Super Acronyms
P.E.D. - P for eigenvectors, E for eigenvalues, D for diagonalization.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Diagonalizable
Definition:
A matrix is diagonalizable if it can be expressed in the form A = PDP⁻¹, where P is a matrix of eigenvectors and D is a diagonal matrix of eigenvalues.
-
Term: Eigenvector
Definition:
A non-zero vector v satisfying the equation Av = λv, where λ is an eigenvalue.
-
Term: Eigenspace
Definition:
The null space of (A - λI), which forms a vector space of eigenvectors corresponding to an eigenvalue.
-
Term: Algebraic Multiplicity
Definition:
The number of times an eigenvalue appears as a root of the characteristic polynomial.
-
Term: Geometric Multiplicity
Definition:
The dimension of the eigenspace associated with an eigenvalue, indicating the number of linearly independent eigenvectors.