Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Eigenvalues and their Importance
Unlock Audio Lesson
Today, we'll start by discussing how to find eigenvalues. Does anyone know what the characteristic equation is?
Isn’t it the determinant of A minus λ times the identity matrix?
Exactly! So, we solve `det(A - λI) = 0` to find the eigenvalues. Remember, the eigenvalues are the values of λ that make this determinant zero.
Can you explain briefly why eigenvalues are important?
Sure! Eigenvalues help us understand important properties of matrices, especially in dynamic systems. They indicate how a system will behave under transformations.
Are there always multiple eigenvalues for matrices?
Not necessarily! Some matrices may have repeated eigenvalues, while others may have distinct ones. This affects the geometric and algebraic multiplicities.
To summarize, Step 1 involves solving the characteristic equation to find the eigenvalues that will guide us in finding the eigenspaces.
Finding Eigenspaces
Unlock Audio Lesson
Now that we have the eigenvalues, let's move to Step 2: Finding the eigenspaces. Can someone tell me how we find an eigenspace for a particular eigenvalue?
Do we solve `(A - λᵢI)v = 0` for each eigenvalue?
Correct! This equation will give us the null space associated with the eigenvalue. Remember, the eigenspace consists of all vectors that satisfy this equation.
What do we do if there’s more than one solution?
Good question! If there are multiple solutions, they will form a vector space. The key is to find a linearly independent set of vectors from this solution space.
So, how does this eigenspace relate to eigenvectors?
The vectors in the eigenspace are indeed the eigenvectors corresponding to the eigenvalue λᵢ. By working through this step, we lay a crucial foundation for the final step.
In summary, Step 2 focuses on calculating the eigenspace for each eigenvalue by solving `(A - λᵢI)v = 0`. This eigenspace contains all eigenvectors corresponding to λᵢ.
Determining the Basis of Eigenvectors
Unlock Audio Lesson
Now, let's discuss Step 3: Determining the basis of the eigenspaces. Once we have the eigenspaces, what do we need to do?
I think we need to extract linearly independent vectors that span the space.
Exactly! This set of linearly independent vectors will represent the basis of eigenvectors for the corresponding eigenvalue.
So, once we've established these basis vectors, what’s next?
Once we have the basis vectors, we can use them to understand the properties of the linear transformation represented by the matrix. They will be very useful in our applications.
Can you remind us why all three steps are necessary?
Sure! Each step interrelates: finding eigenvalues shows us the possible behaviors of `A`, finding eigenspaces gives the sets of vectors for these behaviors, and extracting a basis helps us conceptsually unify these ideas for practical application.
To summarize, Step 3 focuses on extracting a linearly independent basis set from the eigenspaces corresponding to their eigenvalues.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
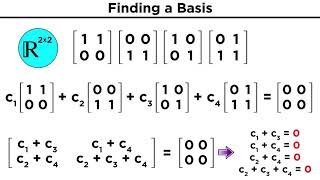
The section introduces three crucial steps to identify the basis of eigenvectors: determining the eigenvalues by solving the characteristic equation, finding the corresponding eigenspaces, and extracting a basis from the eigenspaces. Each step is critical in applications such as structural analysis and dynamic systems in engineering.
Detailed
Detailed Summary
In this section, we outline the Steps to Find Basis of Eigenvectors following a structured approach:
Step 1: Finding Eigenvalues
To begin, we solve the characteristic equation given by det(A - λI) = 0, where A is a square matrix and λ represents the eigenvalues of A. The solutions yield multiple eigenvalues, denoted as λ₁, λ₂, ..., λₖ.
Step 2: Finding Eigenspaces
For each eigenvalue identified in the previous step, we determine its eigenspace by solving the equation (A - λᵢI)v = 0. The null space of this equation represents the eigenspace corresponding to the eigenvalue λᵢ.
Step 3: Determining the Basis
Finally, from the general solutions obtained for the equation, we select a set of linearly independent vectors that span the eigenspace, which ultimately forms the basis of eigenvectors for the respective eigenvalue.
This systematic approach is crucial for applications in engineering fields such as civil engineering where the analysis of structural modes, vibrations, and dynamic behavior of systems are evaluated.
Youtube Videos
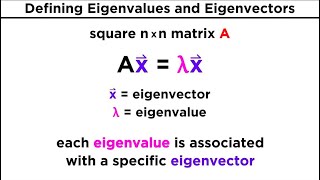
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Step 1: Find the Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solve the characteristic equation:
det(A−λI)=0
This will give the eigenvalues λ₁, λ₂, ..., λₖ.
Detailed Explanation
In this step, we want to find the eigenvalues of a matrix A. To do this, we first set up the characteristic equation, which is derived from the formula for eigenvalues. The eigenvalues are the values of λ that make the determinant of the matrix (A - λI) equal to zero. The solutions to this equation give us all the eigenvalues associated with the matrix.
Examples & Analogies
Think of finding eigenvalues as identifying different resonant frequencies of a musical instrument. Just like how each frequency corresponds to a specific way that the instrument can vibrate, each eigenvalue corresponds to different states the matrix can operate in.
Step 2: Find Eigenspaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For each eigenvalue λᵢ, solve the equation:
(A−λᵢI)v=0
This gives the null space of (A−λᵢI), which is the eigenspace Eᵗ.
Detailed Explanation
After identifying the eigenvalues, the next step is to find the eigenspaces associated with each eigenvalue. We do this by taking each eigenvalue λᵢ and substituting it into the adjusted equation (A - λᵢI)v = 0. The solutions to this equation yield the eigenspace, which is a vector space formed by eigenvectors corresponding to that eigenvalue. Essentially, this tells us all the different directions (vectors) that scale by their eigenvalue when transformed by matrix A.
Examples & Analogies
Imagine you are trying to understand how a particular species of tree grows in various conditions. The eigenvalues represent conditions like sunlight and water availability, and the vectors (eigenvectors) that form the eigenspace illustrate different tree growth patterns corresponding to those conditions.
Step 3: Determine the Basis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
From the general solution of (A−λᵢI)v=0, extract a set of linearly independent vectors that span Eᵗ.
These vectors form the basis of eigenvectors for λᵢ.
Detailed Explanation
In this final step, we focus on the general solution obtained from solving the eigenspace equations. We extract a set of linearly independent vectors from this solution, which can be combined to represent any vector in the eigenspace. The collection of these vectors forms the basis of eigenvectors for that specific eigenvalue λᵢ, illustrating the best set of vectors to describe the matrix's action in that dimension.
Examples & Analogies
Think of this step as finding the best ingredients for a recipe. Just like how each ingredient contributes uniquely and independently to the final dish without redundancy, the linearly independent eigenvectors provide a complete description of the eigenspace without overlap, allowing us to recreate any vector in that space effectively.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalue: A scalar representing the factor by which an eigenvector is stretched.
-
Eigenvector: A vector that changes only in magnitude and not in direction when transformed by a matrix.
-
Eigenspace: The collection of all eigenvectors corresponding to a particular eigenvalue.
-
Basis: A set of vectors that are linearly independent and spans a space.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a matrix A with eigenvalue λ = 4, eigenspace E₄ is computed by solving (A - 4I)v = 0.
-
The characteristic equation for a matrix A might give eigenvalues of λ = 1, 2, and 3, leading to distinct eigenspaces for each.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalues, eigenvectors, linear and true, Find the basis, it’s not hard to do!
📖 Fascinating Stories
-
Imagine a magical forest where each tree represents a matrix. The eigenvalues are the heights of the trees, helping them grow taller in unique ways. The eigenvectors show the direction they sway in the wind, solidifying their paths. To find the forest's best paths, we gather around the tallest trees for guidance.
🧠 Other Memory Gems
-
Remember 'EAF' for Steps: Eigenvalues, Absorb eigenspaces, Find bases. EAF to lead your steps!
🎯 Super Acronyms
Use 'B.E.E.' to remember
- **B**asis
- **E**igenvectors
- **E**igenspaces!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar λ such that for a matrix A, there exists a non-zero vector v where Av = λv.
-
Term: Eigenvector
Definition:
A non-zero vector that, when a linear transformation is applied via a matrix, only scales (and does not change direction).
-
Term: Eigenspace
Definition:
The set of all eigenvectors corresponding to a particular eigenvalue, along with the zero vector.
-
Term: Characteristic Equation
Definition:
An equation obtained from det(A - λI) = 0, used to find eigenvalues.
-
Term: Basis
Definition:
A linearly independent set of vectors that spans a vector space.