Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Absolutely Integrable Functions
Unlock Audio Lesson
Let's start by discussing the first condition for the existence of the Fourier Transform. Can anyone tell me what it means for a function to be absolutely integrable?
Does it mean the integral of the function's absolute value over all time must converge?
Exactly! It means we look at the integral of |f(t)| across the entire real line, and it must be finite. This ensures that the function does not go off to infinity.
So, what happens if the integral is not finite?
Good question! If the integral is infinite, the Fourier Transform cannot be defined. Think of it like trying to capture a signal that keeps growing without bounds.
Is there a way to identify if a function is absolutely integrable?
Yes, you can look for bounds within which the function behaves. For instance, functions that decay rapidly at infinity often are absolutely integrable.
In summary, a function is absolutely integrable If \(\int_{-\infty}^{\infty} |f(t)| dt < \infty\). Let's move on to our next condition.
Finite Discontinuities
Unlock Audio Lesson
Next, let's discuss the second Dirichlet condition: finite discontinuities. Can anyone explain what this means?
It means that within any given interval, the function can only jump a certain number of times, right?
Correct! The function shouldn’t have an infinite number of jumps or discontinuities in any finite interval. This allows us to analyze the function effectively.
Why is this restriction on discontinuities important for the Fourier Transform?
Restricting discontinuities helps avoid complications during transformation. If there were too many jumps, the rapid changes could lead to undefined behavior in the frequency domain.
So again, what does finite mean?
It indicates that we can only allow a manageable number of discontinuities. These conditions help maintain a degree of regularity that is necessary for transformation.
To sum up, the function must have a finite number of discontinuities in any finite interval to ensure it can be transformed successfully.
Finite Number of Maxima and Minima
Unlock Audio Lesson
Finally, let's look at the last condition of Dirichlet’s Conditions—finite maxima and minima. Can someone describe what this entails?
It means the function can only reach a limited number of peaks or troughs in a given interval?
That's right! This condition ensures that the function's oscillation remains bounded, enabling us to examine it properly in frequency terms.
But why is the number of maxima and minima important?
Having too many extremes means rapid oscillations, which complicates the Fourier analysis. We want a function to be well-behaved to confidently perform transformations.
So, if I have a function with an infinite number of peaks, I can't use Fourier Transform?
Exactly! Since it would violate our condition of bounded behavior within finite intervals. To summarize, the function must have a finite number of maxima and minima in any finite interval.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Dirichlet's Conditions specify that a function will have a Fourier Transform if it is absolutely integrable over the entire real line, has a finite number of discontinuities in any finite interval, and a finite number of maxima and minima in any finite interval. These conditions highlight important aspects of function behavior that ensure successful transformation.
Detailed
Conditions for Existence (Dirichlet's Conditions)
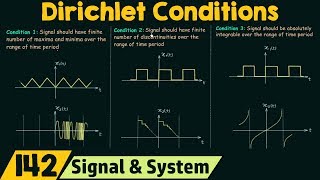
The Fourier Transform is a vital mathematical tool, and its existence is determined by specific conditions known as Dirichlet's Conditions. These are:
- Absolutely Integrable: The function must be integrable, meaning the integral of the absolute value of the function over the entire real line must be finite:
\[\int_{-\infty}^{\infty} |f(t)| dt < \infty \]
- Finite Discontinuities: The function can only have a finite number of discontinuities within any finite interval, ensuring manageable behavior in transformation.
- Finite Extrema: There should be a finite number of maxima and minima within any finite interval, ensuring that the function behaves properly under transformation.
These conditions are sufficient for the existence of the Fourier Transform but are not necessary. The understanding of these conditions is crucial for engineers and scientists as they analyze temporal and spectral data in various applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Condition 1: Absolute Integrability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A function f(t) will have a Fourier Transform if:
1. f(t) is absolutely integrable over (−∞,∞), i.e.,
\[ \int_{-\infty}^{\infty} |f(t)| dt < \infty \]
Detailed Explanation
The first condition states that for a function to have a Fourier Transform, it should be absolutely integrable over the entire real line. This means that when we take the absolute value of the function f(t) and integrate it from negative infinity to positive infinity, the result must be a finite number. In simpler terms, when we look at how 'big' the function gets across its entire range, if the overall area under the curve (considering all values, even if they are negative) is finite, then the function qualifies for a Fourier Transform.
Examples & Analogies
Think of a jar that can hold water. If we pour a certain amount of water (the area under f(t) over time) into the jar, and the jar can hold all of it without overflowing (the integral is finite), then we can say the jar (the function) fits our criteria. If the jar cannot fit all the water we pour (the integral is infinite), then we have a problem, and the function won't have a Fourier Transform.
Condition 2: Finite Discontinuities
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- f(t) has a finite number of discontinuities in any finite interval.
Detailed Explanation
The second condition specifies that the function f(t) can only have a limited number of points where it is not continuous (discontinuities) within any bounded segment of time. Essentially, if we look over any specific interval, there can only be a certain number of 'jumps' or breaks in the function where it does not connect smoothly. This guarantees that despite these breaks, the function does not become too erratic or difficult to handle in terms of analysis.
Examples & Analogies
Imagine driving on a road. If you encounter a few potholes (discontinuities), provided they're manageable and you can navigate around them without too much trouble, you can still make the journey smoothly. But if the road is full of so many potholes that you can't drive safely, then it becomes a problem similar to a function that has too many discontinuities.
Condition 3: Finite Maxima and Minima
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- f(t) has a finite number of maxima and minima in any finite interval.
Detailed Explanation
The third condition requires that within any finite interval of time, the function f(t) should have a limited number of peaks (maxima) and valleys (minima). This means that the function cannot oscillate too wildly; instead, it should have well-defined sections where it reaches high and low values. This requirement ensures that the function remains tractable and can be effectively analyzed with Fourier methods.
Examples & Analogies
Consider a rollercoaster track. If there are only a few rises and dips along the path, the ride can be predictable and manageable. However, if the track had too many sharp rises and drops in a short distance, it would be much more chaotic and difficult to ride smoothly, similar to a function with too many extrema.
Sufficiency of Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These are sufficient but not necessary conditions.
Detailed Explanation
The final point highlights that the conditions listed are sufficient for a function to have a Fourier Transform; however, they are not strictly required. This means that there may be other functions that do not meet all these criteria but can still possess a Fourier Transform. It allows for greater flexibility in which functions can be transformed, highlighting the versatility of the Fourier Transform in handling various kinds of signals.
Examples & Analogies
Think of a recipe for a cake. While following the recipe (meeting the conditions) will guarantee a delicious cake (a function that does have a Fourier Transform), it doesn’t mean that you can’t make a cake just by using some other ingredients and methods. This opens the door to creativity and possibilities beyond standard rules.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Absolutely Integrable: The integral of the absolute value of the function must be finite.
-
Finite Discontinuities: The function can have only a limited number of discontinuities in a finite interval.
-
Finite Maxima and Minima: The function cannot have an infinite number of extreme values in any finite interval.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of an absolutely integrable function is f(t)=e^{-t^2}, as its integral converges over (-∞, ∞).
-
A function like sin(t) is not absolutely integrable because its integral diverges over (-∞, ∞).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
A function to transform must be absolute in form, with jumps that are few, and peaks not askew.
📖 Fascinating Stories
-
Once in the land of Fourier, a function wished to transform. It learned it must be finite, calm, and not swarm.
🧠 Other Memory Gems
-
A mnemonic to remember: A Finite Function Must Meet - Absolutely Integrable, Finite Discontinuities, Maxima & Minima.
🎯 Super Acronyms
Acronym to remember
- **DFM** for **D**irichlet's **F**unction **M**easures.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dirichlet's Conditions
Definition:
A set of conditions that ensure the existence of the Fourier Transform for a given function.
-
Term: Absolutely Integrable
Definition:
A function is said to be absolutely integrable if the integral of its absolute value over the entire real line is finite.
-
Term: Finite Discontinuities
Definition:
A condition indicating that a function can have only a limited number of discontinuities in any finite interval.
-
Term: Maxima and Minima
Definition:
The highest and lowest values of a function within a given interval, respectively.