Differentiation in Time Domain
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Differentiation in Time Domain
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're diving into the differentiation property of the Fourier Transform. Can anyone tell me what differentiation means in a mathematical context?

It means finding the rate at which a function changes.

Exactly! Now, the Fourier Transform relates this concept to frequency representation in an interesting way. When we differentiate a function in time, how do you think that affects its frequency representation?

Does it shift the frequency stuff around?

Not quite a shift. It actually involves multiplying the Fourier Transform by an imaginary component. To recall, if we denote the transformation of a function f(t) in the frequency domain as F(ω), we can write the differentiation as: $$F\left(\frac{d^n f(t)}{dt^n}\right) = (i\omega)^n F(\omega)$$. This means differentiation corresponds to multiplying by $(i\omega)^n$. Remember this as the 'Differentiation Property'!

So differentiating in time domain makes the frequency representation grow or shrink depending on how many times you differentiate!

Precisely! Each time you differentiate, the complexity in the frequency domain increases according to the order of differentiation. Let's summarize: Differentiating f(t) transforms its Fourier representation in a structured, predictable manner.
Applications of Differentiation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've established what the differentiation property is, can anyone think of practical scenarios where this would be essential?

In engineering, maybe in signal processing?

Correct! Signal processing is a prime example. When we have signals that need to be filtered or processed, we often deal with differential equations. By applying the Fourier Transform, we can shift those equations to a simpler form—leading to efficient solutions.

So, it helps to analyze how signals change over time?

Exactly! Analyzing changes in signals quickly leads us to their frequency-content understanding. This separation allows engineers to design better systems by focusing on the critical aspects of signals.

This is really useful when working with vibrations in structures.

That's right! Differentiation also plays a key role in vibration analysis, helping us determine natural frequencies and responses of structures. Let's summarize today: Differentiation is a powerful property that facilitates our work in various engineering applications by simplifying complex time-domain processes into manageable frequency equations.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Differentiation in the time domain is represented in the Fourier Transform framework as a straightforward operation that transforms time-domain differentiation into multiplication by an imaginary frequency in the frequency domain. This property is especially useful in the context of solving differential equations.
Detailed
Differentiation in the Time Domain
Differentiation in the time domain is a key property of the Fourier Transform, enabling us to relate time-based changes in a function to its frequency representation. Specifically, if we differentiate a function multiple times, the Fourier Transform of that differentiated function can be expressed in terms of the Fourier Transform of the original function. Mathematically, this can be expressed as:
$$F\left(\frac{d^n f(t)}{dt^n}\right) = (i\omega)^n F(\omega)$$
This equation reveals that differentiating a function in the time domain corresponds to multiplying its Fourier Transform by $(i\omega)$ raised to the power of the order of differentiation $n$. This fact simplifies the solving of differential equations by transforming them into algebraic equations in the frequency domain. Given that many engineering problems involve such differential equations, understanding this property is vital for efficiently applying the Fourier Transform in practical contexts such as signal processing, control systems, and vibrational analysis. The utility of this property lies in transforming complex time-domain interactions into manageable frequency-domain computations.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fourier Transform of Derivative
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
F{\frac{d^n f(t)}{dt^n}} = (i\omega)^n F(\omega)
Detailed Explanation
This equation shows how the Fourier Transform of a derivative relates to the Fourier Transform of the original function. When we differentiate a function f(t) n times, the Fourier Transform F(ω) gets multiplied by (iω)^n. The imaginary unit i indicates the complex nature of the frequency domain, while ω represents the angular frequency. This is especially helpful when solving differential equations because it allows for transformations that convert derivatives from the time domain into multiplications in the frequency domain.
Examples & Analogies
Imagine you're tracking a car's speed as it moves along a road. When you take the car's position over time and differentiate it, you're essentially measuring how fast the car is going. In the frequency domain, instead of dealing directly with speeds (which would involve continuous measurements), you can now think of those speeds as modifying the original position measurements. Therefore, instead of having to calculate each speed directly at every time point, you can represent that continuous behavior more simply by transforming it to the frequency domain.
Applications in Solving Differential Equations
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This differentiation property is particularly useful in solving differential equations.
Detailed Explanation
The differentiation property of the Fourier Transform allows engineers and scientists to simplify their work when faced with differential equations. By transforming the differential equation into the frequency domain, where derivatives become algebraic expressions (multiplications with (iω)^n), it becomes easier to solve these equations. Once the algebra is complete, they can apply the inverse Fourier Transform to retrieve the solution in the time domain.
Examples & Analogies
Consider a scenario in electrical engineering where you have a circuit with components behaving according to specific rules (like a waterfall). If we treat the circuit's behavior as a differential equation, transforming it with a Fourier Transform is akin to changing your perspective from looking at the waterfall from the side to viewing it from above. This new perspective makes it much easier to see the flow patterns. After solving your problems 'above the waterfall,' you can look back down to get back the actual behavior of your circuit.
Key Concepts
-
Differentiation in Time Domain: Refers to how differentiation of a function can be transformed into frequency domain multiplication.
-
Fourier Transform: A technique for converting a time-based signal into its frequency counterpart.
-
Effect on Frequency Domain: Differentiation in the time domain results in multiplication by $(i\omega)^n$ in the frequency domain.
Examples & Applications
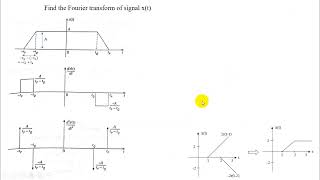
Differentiating a square pulse function results in a function that represents frequency components.
Applying Fourier Transform to solve differential equations in dynamic systems.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When you differentiate, don't you fret, multiply by iω, your success is set!
Stories
Imagine you're an engineer working on a bridge, needing to predict vibrations. Differentiating helps open the door to frequencies, making the complex simple.
Memory Tools
To remember, "Differentiate to 'iω' Multiply" for Fourier Transform.
Acronyms
D-FT — 'Differentiate for Fourier Transform'.
Flash Cards
Glossary
- Differentiation
A mathematical operation that calculates the rate at which a function changes at any given point.
- Fourier Transform
A mathematical transform that converts a time-domain function into a frequency-domain representation.
- Frequency Domain
The domain in which mathematical functions or signals are represented as frequencies.
- Imaginary Unit (i)
A mathematical constant defined as the square root of -1.
- Complex Exponential
An expression involving the exponentiation of an imaginary number.
Reference links
Supplementary resources to enhance your learning experience.
