Fourier Transform of Rectangular Pulse
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Rectangular Pulse Function
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re delving into the Fourier Transform of a rectangular pulse. Does anyone know what a rectangular pulse looks like?

Isn't it like a simple square wave, where the signal is constant for a certain time and then drops?

Exactly! It’s defined as 1 for a certain width T and 0 otherwise. This function is crucial in signal processing. It simulates on-off signals like those in communication systems.

So, how do we relate this time-domain function to its frequency representation?

Great question! We achieve this through its Fourier Transform. Let’s take a closer look at the definition and how to compute this transform.
Deriving the Fourier Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We want to derive the Fourier Transform for our function, which is defined as: f(t) = 1 for |t| ≤ T/2. Can anyone tell me how we begin?

Don’t we use the integral from -T/2 to T/2?

Precisely! We express it mathematically: F(ω) = ∫ from -T/2 to T/2 of e^{-iωt} dt. Who can compute this integral?

I think we use integration techniques. After integrating, we get back a sine function that helps us derive the final answer!

Exactly! And the result is F(ω) = T·sinc(ωT/2π). This shows how the rectangular pulse transforms into the sinc function in the frequency domain.
Understanding the Significance of the Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Why do you think understanding the Fourier Transform of the rectangular pulse is important in engineering?

It helps engineers analyze signals better! If we know the shape in the frequency domain, we can predict behavior in real systems.

Correct! It’s used in communication systems to filter signals and reconstruct them. Any other applications you can think of?

Maybe in audio processing? Like how sound is sampled and modified?

Exactly! The Fourier Transform plays a central role in various fields, including audio and signal computation. End the day by remembering how time and frequency domains interrelate.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section elaborates on the rectangular pulse function and provides a full derivation of its Fourier Transform, showing how the time-domain rectangular pulse translates into its frequency-domain representation. This transformation underpins many applications in engineering.
Detailed
Fourier Transform of Rectangular Pulse
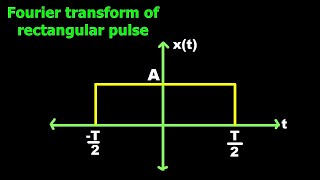
In this section, we examine the Fourier Transform of a rectangular pulse, defined mathematically. The rectangular pulse function is expressed as:
$$
f(t) = \begin{cases}
1, & |t| \leq T/2 \
0, & \text{otherwise}
\end{cases}
$$
This function has a width of T. The Fourier Transform of this function is calculated using the integral:
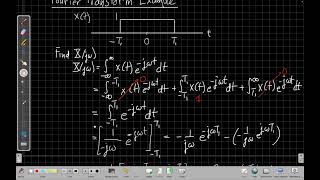
$$
F(\omega) = \int_{-T/2}^{T/2} e^{-i\omega t} dt
$$
Evaluating this integral leads to:
$$
F(\omega) = T \cdot \text{sinc}\left(\frac{\omega T}{2\pi}\right)
$$
where the sinc function is defined as:
$$
\text{sinc}(x) = \frac{\sin(\pi x)}{\pi x}.
$$
The significance of this transformation lies in its foundational role in signal processing and communication systems, enabling engineers to analyze how signals behave in different frequency domains.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Rectangular Pulse
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let
f(t)={
1 / 2,
|t|≤ T
0,
otherwise
This is a rectangular pulse of width T.
Detailed Explanation
In this chunk, we define a function called f(t) that represents a rectangular pulse. The function f(t) is equal to 1/2 when the absolute value of t is less than or equal to T, which means the rectangular pulse has a width of T. Outside this interval, the function is zero. This creates a 'pulse' shape where the signal has a constant value (1/2) for a specific duration (T) and is silent (0) outside this duration.
Examples & Analogies
Imagine turning on a flashlight for a set period (T). When the flashlight is on, the light is bright (1/2), representing our rectangular pulse. The moment you turn it off, the light goes out (0), similar to the function's behavior outside of the interval. This on-and-off behavior is akin to a rectangular pulse in signal processing.
Fourier Transform Calculation
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Fourier Transform:
F(ω)=∫−T/2T/2exp(−iωt)dt=
[exp(−iωt)]−T/2T/2
=F(ω)=T·sinc(ωT/2)(1/(2π))
Detailed Explanation
This chunk presents the calculation of the Fourier Transform of the rectangular pulse function f(t). The Fourier Transform F(ω) is found by integrating the function multiplied by e^(-iωt) over the interval from -T/2 to T/2. After performing the integration and applying the limits, we find that F(ω) equals T times the sinc function evaluated at ωT/2, normalized by (1/(2π)). This mathematical representation allows us to express how the rectangular signal is represented in the frequency domain, highlighting where its frequencies lie.
Examples & Analogies
If you've ever played a guitar and struck a string, you might notice that the sound resonates at the fundamental frequency and its harmonics. Just as those specific frequencies create the sound, the Fourier Transform highlights which frequencies are present in the rectangular pulse, showing us how the pulse can be viewed and analyzed through its frequency components.
Understanding sinc Function
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
where sinc(x)=sin(πx)/(πx)
Detailed Explanation
In this chunk, we define the sinc function, which is crucial in the context of Fourier Transforms. The sinc function is defined as sin(πx)/(πx). This function is important because it describes the frequency response of the rectangular pulse. The sinc function has a distinctive shape that oscillates, with zeros occurring at regular intervals, indicating that specific frequencies are present due to the finite width of the rectangular pulse.
Examples & Analogies
Imagine tossing a pebble into a still pond. The ripples that spread out represent the sinc function, which also shows peaks and troughs. Just as the intensity of the ripples decreases with distance from the source, the peaks of the sinc function indicate how the energy of the rectangular pulse is distributed across different frequencies. This visual analogy helps to connect the concept of the sinc function with a physical phenomenon.
Key Concepts
-
Rectangular Pulse: A basic signal often used in time-domain analysis.
-
Fourier Transform: A method for analyzing frequency content of signals.
-
Sinc Function: Integral result of the Fourier Transform for a rectangular pulse.
Examples & Applications
Example 1: The rectangular pulse serves as a model for an on-off switch in electronic circuits.
Example 2: Used in communication theory, analyzing how broadband signals transform.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When you see a pulse so square, frequency's sinc will be there.
Stories
Imagine a light switch that stays on only for a moment. This on-off action is like the rectangular pulse, and as we analyze its effects in signals, the sinc function reveals hidden frequency patterns.
Memory Tools
To remember the transform, think: 'Rectangle to Sinc, Follows the frequency link.'
Acronyms
FTRP
Fourier Transform Rectangular Pulse.
Flash Cards
Glossary
- Rectangular Pulse
A function that is equal to one for a specific interval of time and zero otherwise.
- Fourier Transform
A mathematical transformation that converts a function into its frequency domain representation.
- Sinc Function
Defined as sinc(x) = sin(πx)/(πx), it arises in the Fourier Transform of the rectangular pulse.
Reference links
Supplementary resources to enhance your learning experience.
