Time Scaling
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Time Scaling
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to understand the time scaling property of the Fourier Transform. This property allows us to manipulate a time-domain function and see how it affects its frequency representation. Can anyone tell me what they think 'scaling' might mean in this context?

I think it means changing the speed of the signal, like making it play faster or slower?

Exactly! When we scale a function in time, we are essentially speeding it up or slowing it down. For example, if we said f(2t), we are compressing the function in the time domain. This has a specific impact on our frequency domain.

So what happens to the frequencies in that case?

Great question! The frequencies stretch or compress in accordance with the time scaling. The relationship can be expressed mathematically, which we will dive into next.
Exploring the Mathematical Expression for Time Scaling
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

The mathematical representation of time scaling in Fourier Transform is: F{f(at)} = (1/|a|) F(ω/|a|). What do you think |a| indicates here?

Isn't it the absolute value of 'a'? But why do we need that?

Correct! The absolute value ensures we consider the scaling consistently, regardless of whether 'a' is positive or negative. A positive 'a' compresses the function, while a negative one flips it. It helps us maintain the integrity of our analysis. Why do you think this property is important?

I guess it helps when we want to analyze signals of different speeds?

Perfect! Being able to analyze and interpret the frequency changes due to time scaling is essential in many engineering applications.
Practical Applications of Time Scaling
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss where this time scaling property can be applied. For instance, how can engineers benefit from understanding this concept?

They could use it for signal processing during audio production, right?

Correct! In audio processing, understanding how changing a signal’s duration affects its frequency helps engineers manipulate sound effectively. Additionally, in data analysis, how might it apply?

It could help with data collected over different sampling rates, making the frequency domain easier to work with.

Exactly! The time-scaling property allows the adjustment of signals for coherent analysis across different applications, such as sensor data in civil engineering.
Review of Key Concepts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s wrap up by summarizing the key points we've discussed about time scaling. Who can explain what time scaling means for a function in the time domain?

It means stretching or compressing the function, which affects the frequency domain representation.

Exactly! And how do we express time scaling mathematically in the Fourier Transform?

F{f(at)} = (1/|a|) F(ω/|a|)!

Great job! Understanding these properties helps engineers analyze signals efficiently. Make sure you review these concepts as they are foundational for our upcoming topics.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
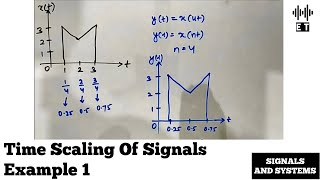
In this section of the chapter, we explore the time scaling property of the Fourier Transform, which indicates that scaling a time-domain function changes the frequency-domain representation accordingly. Understanding this property is vital for analyzing signals and systems efficiently.
Detailed
Time Scaling
In the study of the Fourier Transform, the time scaling property plays a crucial role in understanding how changes in the time-domain representation affect its corresponding frequency-domain representation. Specifically, if a function is scaled in time by a factor, it results in the compression or stretching of its frequency representation. This can be mathematically expressed as:
$$F\{f(at)\} = \frac{1}{|a|} F\left(\frac{\omega}{|a|}\right)$$
where a is the scaling factor and F(ω) is the Fourier Transform of the original function f(t). This property is significant in various applications, especially when dealing with signal processing and analysis, as it offers a way to manipulate signals efficiently without needing to redefine them entirely. Understanding time scaling enhances our overall competence in working with Fourier Transforms and applying them in practical contexts.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Time Scaling
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
1
F{f(at)}= F
(ω)
|a|
a
Scaling the time domain compresses or stretches the frequency domain.
Detailed Explanation
Time scaling refers to the effect of changing the time variable in a function on its Fourier Transform. When we apply a scaling factor 'a' to the time variable, denoted as 'f(at)', it leads to a modification in the corresponding frequency representation. Specifically, the frequency domain representation gets scaled by the inverse of the absolute value of 'a'. This means if we stretch the time signal (put in a larger 'a'), the frequency representation will compress, and vice versa.
Examples & Analogies
Imagine you are watching a video on fast forward; everything happens quicker, and the background music speeds up. This is similar to compressing the time domain: actions happen in less time, and their frequency increases, resulting in a higher pitch in sound. Conversely, if you slow down the video, actions take longer, and the music’s pitch drops.
Impact of Scaling
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Scaling the time domain compresses or stretches the frequency domain.
Detailed Explanation
When a function is compressed in the time domain (for example, if 'a' is greater than 1), it leads to a wider range of frequencies in the frequency domain. Conversely, stretching the function (when 'a' is between 0 and 1) means that the frequencies become narrower. This relationship is fundamental as it helps us understand how different elements of a signal's characteristics are interrelated through Fourier Transforms.
Examples & Analogies
Think about how a rubber band works. If you stretch a rubber band (making it thinner and longer), it vibrates more slowly when plucked, producing a lower frequency sound. However, if you squeeze it (compressing it), it vibrates faster and creates a higher frequency sound. In the same way, how we scale time affects the wavelength and frequency of signals.
Key Concepts
-
Time Scaling: Altering a function’s time variable changes its frequency representation.
-
Frequency Domain Representation: Analyzing signals in terms of their frequency components can be achieved through the Fourier Transform.
Examples & Applications
If f(t) = sin(t), then f(at) = sin(at) compresses the time signal and spreads out its frequencies.
With a time scaling factor of a=2, the Fourier Transform representation will show frequencies compressed by the factor of 2.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When time is scaled, don't fear the sound, frequencies stretch or compress all around.
Stories
Imagine a musician speeding up their song. As they play faster, the notes get higher, representing how time scaling affects music just like Fourier Transform affects signals.
Memory Tools
Remember: Caps (C) for Compress, and Stretched (S) for Stretch – Time Scaling Changes the Spectrum (TCCS).
Acronyms
TST
Time Scaling Transforms help understand the frequency!
Flash Cards
Glossary
- Time Scaling
The process of altering the time variable in a function which affects its representation in the frequency domain.
- Fourier Transform
A mathematical transformation that converts a function of time into a function of frequency.
- Frequency Domain
The representation of a signal in terms of its frequency components rather than its time components.
Reference links
Supplementary resources to enhance your learning experience.
