Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Cosine and Sine Transforms
Unlock Audio Lesson
Today, we're going to explore the Fourier Cosine Transform and the Fourier Sine Transform. These are used when we have a function defined only on the interval from zero to infinity. Can anyone tell me why we might want to use transforms that only consider this interval?
Well, some physical phenomena, like heat conduction, often start from zero time and extend to infinity.
Exactly! Good observation. In such cases, we look for even properties, and that's where the cosine function comes in, while the sine function helps us consider odd properties. Let's start with the Fourier Cosine Transform.
Formulas of Fourier Cosine Transform
Unlock Audio Lesson
"The formula for the Fourier Cosine Transform is:
Formulas of Fourier Sine Transform
Unlock Audio Lesson
"The Fourier Sine Transform focuses on odd functions. It is defined as:
Applications in Engineering
Unlock Audio Lesson
These transforms are vital in solving boundary value problems. For instance, what applications can you think of in civil engineering where these transforms might be used?
Maybe in analyzing the heat flow in beams?
Yes, and also in vibration analysis of bridges!
Perfect! Both examples illustrate how these transforms support practical engineering challenges. In essence, they allow us to transform physical problems into mathematical forms we can solve easily.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the definitions and formulas for the Fourier Cosine and Sine Transforms, including their respective inverses. These transforms are crucial in applications, particularly in civil engineering, for solving boundary value problems such as heat flow and vibrations.
Detailed
In the Fourier Cosine and Sine Transforms section, we explore the foundational definitions of both transforms used when a function is defined only on the interval from 0 to infinity. The Fourier Cosine Transform is defined as:
F_c(ω) = (2/π) ∫_0^∞ f(t) cos(ωt) dt
This transforms a time-domain function into its frequency-domain representation focusing on even properties. The Inverse Fourier Cosine Transform is given by:
f(t) = (2/π) ∫_0^∞ F_c(ω) cos(ωt) dω
Similarly, the Fourier Sine Transform is defined as:
F_s(ω) = (2/π) ∫_0^∞ f(t) sin(ωt) dt
And its inverse:
f(t) = (2/π) ∫_0^∞ F_s(ω) sin(ωt) dω
These transforms play a significant role in various applications in civil engineering, particularly in solving boundary value problems such as heat flow through semi-infinite slabs and vibrations of beams, making them essential tools for engineers and applied scientists.
Youtube Videos
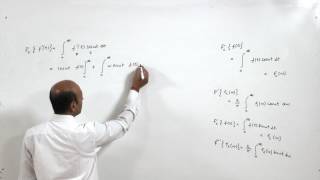
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fourier Cosine and Sine Transforms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When the function is defined only on [0,∞), we often use Fourier Cosine Transform (FCT) and Fourier Sine Transform (FST).
Detailed Explanation
The Fourier Cosine Transform (FCT) and Fourier Sine Transform (FST) are specific types of Fourier Transforms used when dealing with functions that are defined only on the interval from 0 to infinity. This is particularly useful in scenarios where you do not need to analyze signals that extend in the negative time direction.
Examples & Analogies
Imagine tracking the heat flow in a metal rod that has been heated from one end but not considering how it cooled before heating started; this situation reflects a scenario where only positive time values, or physical scenarios like heat flow, are relevant.
Fourier Cosine Transform (FCT)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fourier Cosine Transform
\[ F_c(ω) = \frac{2}{\pi} \int_{0}^{\infty} f(t)\cos(ωt) dt \]
Detailed Explanation
The Fourier Cosine Transform is defined as a specific integral. It transforms the function f(t), which is defined for t from 0 to infinity, into frequency domain representation F_c(ω). The cosine function in the integral helps capture the even symmetry of the function being transformed, which is particularly beneficial for certain physical problems, especially those that exhibit symmetry.
Examples & Analogies
Think of sound waves generated by a vibrating string fixed at both ends. The oscillation pattern is symmetric, and the Fourier Cosine Transform helps analyze those patterns effectively in terms of frequency.
Inverse Fourier Cosine Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Inverse Fourier Cosine Transform
\[ f(t) = \frac{2}{\pi} \int_{0}^{\infty} F_c(ω)\cos(ωt) dω \]
Detailed Explanation
The Inverse Fourier Cosine Transform allows you to reconstruct the original function f(t) from its frequency representation F_c(ω). This means, knowing the frequency components of the function, you can go back and determine the time-domain function. The integral incorporates the same cosine function, ensuring that this transform correctly reassembles the original signal.
Examples & Analogies
It's like tuning a radio to get back to your favorite song. You know the song's frequency (the spectrum) and tuning back to that frequency allows you to hear the song clearly again (the original function).
Fourier Sine Transform (FST)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fourier Sine Transform
\[ F_s(ω) = \frac{2}{\pi} \int_{0}^{\infty} f(t)\sin(ωt) dt \]
Detailed Explanation
The Fourier Sine Transform is similar to the Fourier Cosine Transform, but it uses the sine function to represent the function f(t) in the frequency domain F_s(ω). Sine transforms are particularly useful when the function you are examining has certain odd symmetry properties or when you're only interested in the odd part of the signal.
Examples & Analogies
Consider the sound wave produced by an organ pipe. The harmonic components can be analyzed using the Fourier Sine Transform, capturing the essence of how sound travels through the air.
Inverse Fourier Sine Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Inverse Fourier Sine Transform
\[ f(t) = \frac{2}{\pi} \int_{0}^{\infty} F_s(ω)\sin(ωt) dω \]
Detailed Explanation
The Inverse Fourier Sine Transform reverses the Fourier Sine Transform process, allowing us to recover the original function f(t) from its sine transform F_s(ω). This ensures that all the information in the frequency domain captured by sine waves can be used to recreate the original function.
Examples & Analogies
Just like reconstructing a puzzle from pieces, if you have the sine components of a complex wave, you can put them together to form the original signal again.
Applications of Fourier Cosine and Sine Transforms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These transforms are commonly applied in solving boundary value problems in civil engineering (e.g., heat flow through semi-infinite slabs, vibration of beams).
Detailed Explanation
Fourier Cosine and Sine Transforms are particularly useful in scenarios like calculating heat distribution along materials that are only partially exposed (like a half-infinite slab) or analyzing vibrations along structures like beams where the analysis only concerns one side. These transforms simplify the equations, making it easier to solve boundary value problems encountered in civil engineering.
Examples & Analogies
Think about how engineers need to evaluate how a bridge will respond to wind forces. By using Fourier Sine and Cosine Transforms, they can visualize and analyze the oscillation patterns of the bridge's structure under those forces, ensuring safety and durability.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fourier Cosine Transform: Used for functions defined on [0, ∞) to analyze even properties.
-
Fourier Sine Transform: Used for functions defined on [0, ∞) to analyze odd properties.
-
Inverse Transforms: Allows retrieval of original functions from their frequency representations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of using the Fourier Cosine Transform to solve a heat conduction problem.
-
Example of the Fourier Sine Transform applied in vibration mode analysis of a beam.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Fourier sine and cosine, odd and even in their design!
📖 Fascinating Stories
-
Imagine two friends, Sine and Cosine, representing odd and even functions; they help engineers understand the world in terms of frequency.
🧠 Other Memory Gems
-
Remember: COSine is for Even (like a mirror), and SINe is for Odd (like a wave).
🎯 Super Acronyms
FCT
- Frequency change through Cosine Transformation; FST
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Cosine Transform (FCT)
Definition:
A transform used to convert a function defined on [0, ∞) into its frequency-domain representation using cosine functions.
-
Term: Fourier Sine Transform (FST)
Definition:
A transform used to convert a function defined on [0, ∞) into its frequency-domain representation using sine functions.
-
Term: Inverse Fourier Cosine Transform
Definition:
A formula used to retrieve the original time-domain function from its cosine transform.
-
Term: Inverse Fourier Sine Transform
Definition:
A formula used to retrieve the original time-domain function from its sine transform.
-
Term: Boundary Value Problems
Definition:
Problems in mathematical analysis where one seeks to find solutions to differential equations with specific conditions at the boundaries.