Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Frequency Shifting
Unlock Audio Lesson
Today, we are going to explore frequency shifting, a fundamental concept in Fourier analysis. Who can tell me what happens to a signal when we multiply it by a complex exponential?
Does it change the signal itself?
Good question! While the original time-domain signal remains unchanged, its representation in the frequency domain shifts. This is crucial in signal processing. For instance, multiplying by $e^{iω_0 t}$ shifts the spectrum by $ω_0$. Remember: 'Multiply and shift!'
What does multiplying by a complex number do to the function?
Great follow-up! Multiplying by a complex exponential introduces a phase shift but does not affect the amplitude of the signal.
Can you give an example where this is useful?
Certainly! Frequency shifting is invaluable in communication systems for modulating signals. It's like changing the channel on a radio; you’re tuning into different parts of the spectrum.
Applications of Frequency Shifting
Unlock Audio Lesson
Now, let’s discuss applications. Can anyone think of a field where frequency shifting is applied?
What about in music or audio processing?
Exactly! Frequency shifting allows us to change pitches or tones in audio signals without affecting the rhythm. This technique is widely used in synthesizers.
Are there other fields?
Yes, it’s also used in radar and telecommunications for transmitting signals over designated frequencies to avoid interference. So, architecting with frequencies allows complex systems to operate efficiently!
Mathematical Understanding of Frequency Shifting
Unlock Audio Lesson
Let’s look at the math behind this. When we take the Fourier Transform of $e^{iω_0 t} f(t)$, what do we expect in the transformed domain?
It looks like it would shift the whole spectrum.
Correct! This can be represented as $F(ω - ω_0)$. It’s crucial for integrating signals across boundaries.
Why does the frequency shift occur?
When we multiply $f(t)$ by $e^{iω_0 t}$, it introduces an oscillation that moves all frequency components of $f(t)$ by $ω_0$. Visualize it as riding on a wave, shifting up or down the spectrum.
Understanding the Role of Shifting in Signal Processing
Unlock Audio Lesson
To wrap up, let’s look at how frequency shifting integrates into signal processing. Can anyone summarize its benefits?
It helps isolate certain frequencies for analysis or modification without altering the entire signal.
Well said! Isolation of frequencies allows precise manipulation, crucial in filtering and equalization. Remember: 'Shift for clarity!'
What are some challenges one might face with frequency shifting?
An excellent point! One main challenge is potential aliasing if frequencies are not managed correctly. Thus, maintaining a proper sampling rate is essential.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores the concept of frequency shifting in the context of Fourier Transforms. It describes how multiplying a time-domain signal by a complex exponential leads to a corresponding shift in its frequency domain representation, enabling various applications in signal processing.
Detailed
Frequency Shifting
Frequency shifting is a pivotal concept in Fourier analysis, essential for understanding the manipulation of signals in the frequency domain. When a function $f(t)$ undergoes frequency shifting by multiplying it with a complex exponential $e^{i heta t}$, its Fourier transform shifts accordingly. Mathematically, this is expressed as:
$$F\{e^{iω_0 t} f(t)\} = F(ω - ω_0)$$
The significance of this property lies in its application in various engineering fields, particularly in signal processing, where shifting the frequency spectrum allows easier manipulation and analysis of signal characteristics. This transformation is utilized extensively in modulation and demodulation processes in communication systems, frequency filtering, and even in solving differential equations dynamically.
Youtube Videos
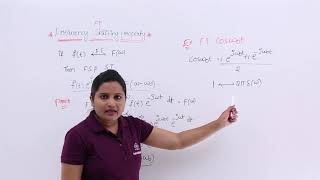
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Frequency Shifting Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
F{eiω0tf(t)}=F(ω−ω0)
Detailed Explanation
Frequency shifting refers to the effect that multiplying a time-domain signal by a complex exponential has on its Fourier Transform. The equation given indicates that the Fourier Transform of a product of a complex exponential and a function results in a shift of the function's frequency spectrum. Specifically, if you have a function f(t) and you multiply it by eiω0t, the resulting Fourier Transform will be shifted by ω0 in the frequency domain.
Examples & Analogies
Imagine you have a radio tuned to a specific frequency where a music station broadcasts. If a new station starts transmitting at a slightly different frequency, you would need to adjust (or shift) your radio's dial to catch that station. In this analogy, multiplying f(t) by eiω0t shifts your 'dial' in the frequency domain to capture different frequencies of the signal.
Impact of Frequency Shifting
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Multiplication by a complex exponential in time domain shifts the frequency spectrum.
Detailed Explanation
When you multiply a time-domain signal by an exponential decay or growth, it alters how the signal is represented in the frequency domain. Essentially, this operation helps in analyzing how signals behave at different frequency levels. For example, if you want to isolate or enhance a particular frequency component of a signal, applying frequency shifting allows you to do so effectively.
Examples & Analogies
Consider a filter you might use to separate different instruments in an orchestra. By shifting the frequencies, you can emphasize the sound of the violin while diminishing the presence of the drums, making it easier to focus on one particular sound amidst the ensemble.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Frequency Shifting: A method to modify the frequency characteristics of signals.
-
Fourier Transform: The process of converting signals from the time domain to the frequency domain.
-
Complex Exponential: A mathematical function crucial for frequency shifting.
-
Spectrum Shift: The alteration of the frequency spectrum due to mathematical transformations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In communication systems, frequency shifting is used to translate a message signal into a specific frequency band.
-
Musical synthesizers apply frequency shifting to create different tones while maintaining the same rhythmic structure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When signals shift and frequencies blend, communication flows without an end.
📖 Fascinating Stories
-
A radio station wants to play music for all. To avoid mix-ups, they shift frequencies to stand tall, allowing everyone to enjoy the call.
🧠 Other Memory Gems
-
S.I.F.T: Shift Is Frequency Transformation!
🎯 Super Acronyms
S.F.T
- Signal Frequency Transformation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Frequency Shifting
Definition:
A process that modifies the frequency spectrum of a signal via multiplication by a complex exponential.
-
Term: Fourier Transform
Definition:
A mathematical transform that converts a time-domain signal into its frequency-domain representation.
-
Term: Complex Exponential
Definition:
An expression of the form $e^{iθ}$, where $θ$ is a phase angle, often used in frequency shifting.
-
Term: Spectrum
Definition:
The range of frequencies present in a signal.