Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Cosine Transform
Unlock Audio Lesson
Today we're diving into the Fourier Cosine Transform. Can anyone tell me what the Fourier Transform does generally?
Isn't it a method to convert time-domain signals into frequency-domain?
Exactly! Now, the Fourier Cosine Transform is specific to functions defined on [0, ∞). Its formula is $$F_c(ω) = \frac{2}{\pi} \int_0^{\infty} f(t) \cos(ωt) dt$$. Can anyone summarize what this means?
It transforms a function into its frequency component using cosine.
Well said! Remember, this transform is essential when we're dealing with positive time signals. Let's explore why it matters in civil engineering.
Applications of the Fourier Cosine Transform
Unlock Audio Lesson
The Fourier Cosine Transform is particularly useful in solving problems like heat flow through semi-infinite slabs. Does anyone know how it applies in that context?
I guess it helps in modeling how heat spreads in materials?
Right! Its ability to analyze frequency components aids in predicting how structures respond to heat. Can anyone cite another application?
It could be used to analyze vibrations in beams and other structures.
Yes! It plays a vital role in modal analysis and evaluating natural frequencies, enhancing our design strategies.
Inverse Fourier Cosine Transform
Unlock Audio Lesson
Now, who can explain the inverse Fourier Cosine Transform?
Isn't it the formula that recovers the original function from its Fourier Cosine Transform?
Exactly! It’s given by $$f(t) = \frac{2}{\pi} \int_0^{\infty} F_c(ω) \cos(ωt) dω$$. Why is this important in engineering contexts?
It helps us go back from frequency analysis to the original function to understand real-world behavior.
Spot on! Knowing both the forward and inverse transforms ensures full analysis capabilities for engineers.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the Fourier Cosine Transform (FCT) and its inverse. It explains how the FCT transforms functions defined only on the interval [0, ∞) into the frequency domain, emphasizing its application in civil engineering problems such as heat flow and vibrations.
Detailed
Fourier Cosine Transform
The Fourier Cosine Transform (FCT) is utilized for functions limited to the domain [0, ∞). It is significant in applications requiring the analysis of periodic or non-periodic phenomena, particularly in engineering disciplines such as civil engineering. Defined as:
$$F_c(ω) = \frac{2}{\pi} \int_0^{\infty} f(t) \cos(ωt) dt$$
The inverse is given by:
$$f(t) = \frac{2}{\pi} \int_0^{\infty} F_c(ω) \cos(ωt) dω$$
The Fourier Cosine Transform is crucial for solving boundary value problems, such as heat distribution in solids or vibrations of beams, showcasing its importance in real-world applications.
Youtube Videos
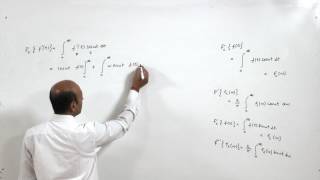
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fourier Cosine Transform Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Fourier Cosine Transform is defined as:
$$
F_c(ω) = \frac{2}{\pi} \int_{0}^{\infty} f(t) \cos(ωt) dt
$$
Detailed Explanation
The Fourier Cosine Transform (FCT) is a mathematical operation that transforms a function defined over the interval from 0 to infinity into the frequency domain. In simple terms, it helps us analyze the frequencies contained in a function. Here, \( f(t) \) is the original function we want to analyze, and \( ω \) represents the frequency. The integral computes how much of each frequency is present in the function by multiplying it with \( \cos(ωt) \) and integrating it over all time from 0 to infinity.
Examples & Analogies
Think of the Fourier Cosine Transform like a chef tasting a soup to identify its flavors. Just as the chef uses different tasting techniques to detect various ingredients, the Fourier Cosine Transform analyzes a signal to pick out the frequencies that make up that signal, revealing what 'ingredients' are present in terms of frequency.
Inverse Fourier Cosine Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Inverse Fourier Cosine Transform is defined as:
$$
f(t) = \frac{2}{\pi} \int_{0}^{\infty} F_c(ω) \cos(ωt) dω
$$
Detailed Explanation
The Inverse Fourier Cosine Transform is the process of converting a frequency-domain representation back into the original time-domain function. It takes the transformed function \( F_c(ω) \) and uses it to reconstruct \( f(t) \) by integrating over all frequencies. This operation is essential in signal processing, allowing engineers to retrieve the original signal after analyzing its frequency components.
Examples & Analogies
Consider the inverse process like a musician playing notes to reconstruct a song after hearing its chords. Each frequency component contributes to the final sound. The Inverse Fourier Cosine Transform takes all those frequency 'notes' and combines them to recreate the original signal, just as the musician combines notes to play a complete piece of music.
Applications of Fourier Cosine Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Fourier Cosine Transform is commonly applied in solving boundary value problems in civil engineering (e.g., heat flow through semi-infinite slabs, vibration of beams).
Detailed Explanation
In civil engineering, the Fourier Cosine Transform is utilized in various practical scenarios, particularly when solving complex problems. For example, when analyzing heat conduction in materials such as slabs, where the heat flow needs to be examined over time, the FCT helps convert the temperature distribution problem into a manageable frequency domain problem, simplifying the calculations. Similarly, it is helpful in studying vibrations in beams and structures, allowing engineers to predict how these materials react under different conditions.
Examples & Analogies
Imagine an architect designing a bridge. By using the Fourier Cosine Transform, the architect can enhance the design by analyzing how the bridge will react to different loads and pressures over time, similar to how a soccer coach uses data analytics to assess players' performances and energies during a game to improve strategies.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fourier Transform: A method for transforming a function from its time domain to the frequency domain.
-
Fourier Cosine Transform (FCT): A specific Fourier Transform for functions defined only on [0, ∞).
-
Inverse Fourier Cosine Transform: The operation to recover a function from its cosine transform.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In the heat flow problem in civil engineering, the Fourier Cosine Transform is utilized to model temperature distribution in a semi-infinite slab.
-
In vibration analysis, the FCT helps assess how a structure responds to dynamic loads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To flow the heat or catch the vibe, Cosine Transform you must imbibe!
📖 Fascinating Stories
-
Imagine an engineer testing a beam that’s shaking; using the Fourier Cosine Transform, they understand its making.
🧠 Other Memory Gems
-
COT: Cosine, Original function, Time domain - remember the basics every time!
🎯 Super Acronyms
FCT
- Fourier Cosine Transform - a tool for timeless analysis!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Cosine Transform (FCT)
Definition:
A specific Fourier transform used for functions defined only on the interval [0, ∞), representing the function in terms of its cosine frequency components.
-
Term: Inverse Fourier Cosine Transform
Definition:
A mathematical operation that recovers the original function from its Fourier Cosine Transform using cosine frequencies.
-
Term: Boundary Value Problems
Definition:
Mathematical problems where a differential equation needs to be solved with specific conditions at the boundaries.